贝叶斯算法

1. 贝叶斯定理相关公式

      a. 先验概率P(A)：在不考虑任何情况下，A事件发生的概率

      b. 条件概率P(B|A)：A事件发生的情况下，B事件发生的概率

      c. 后验概率P(A|B)：在B事件发生之后，对A事件发生的概率的重新评估

      d. 全概率：如果A和A'构成样本空间的一个划分，那么事件B的概率为：A和A'的概率分别乘以B对这两个事件的概率之和。
      

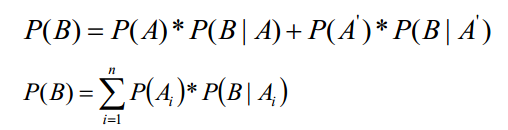
2. 贝叶斯定理公式

          

 

3. 贝叶斯公式成立的前提条件

       样本空间中对象是互斥的，这些对象发生的概率相加为1。

 

4. 朴素贝叶斯算法推导   

          

5. 朴素贝叶斯算法流程

       朴素贝叶斯算法流程/定义如下：
       设x={a1,a2,...,am}为待分类项，其中a为x的一个特征属性
       类别集合为C={y1,y2,...,yn}
       分别计算P(y1|x),P(y2|x),....,P(yn|x)的值（贝叶斯公式）
       如果P(yk|x)=max{P(y1|x),P(y2|x),....,P(yn|x)},那么认为x为yk类型
 

5. 高斯贝叶斯公式

        

6. 伯努利朴素贝叶斯
       

 

7. 多项式朴素贝叶斯
           

 

8.  贝叶斯网络

            把某个研究系统中涉及到的随机变量，根据是否条件独立绘制在一个有向图中，就形成了贝叶斯网络。贝叶斯网络(Bayesian Network)，又称有向无环图模型(directed acyclicgraphical model, DAG)，是一种概率图模型，根据概率图的拓扑结构，考察一组随机变量{X1,X2,...,Xn}及其N组条件概率分布(Conditional ProbabililtyDistributions, CPD)的性质.

当多个特征属性之间存在着某种相关关系的时候，使用朴素贝叶斯算法就没法解决这类问题，那么贝叶斯网络就是解决这类应用场景的一个非常好的算法。

一般而言，贝叶斯网络的有向无环图中的节点表示随机变量，可以是可观察到的变量，或隐变量，未知参数等等。连接两个节点之间的箭头代表两个随机变量之间的因果关系(也就是这两个随机变量之间非条件独立)，如果两个节点间以一个单箭头连接在一起，表示其中一个节点是“因”，另外一个是“果”，从而两节点之间就会产生一个条件概率值。

注意：每个节点在给定其直接前驱的时候，条件独立于其后继。这里的有向图是单向的。

 

贝叶斯网络判定条件独立-01 
                 

贝叶斯网络判定条件独立-02
                 

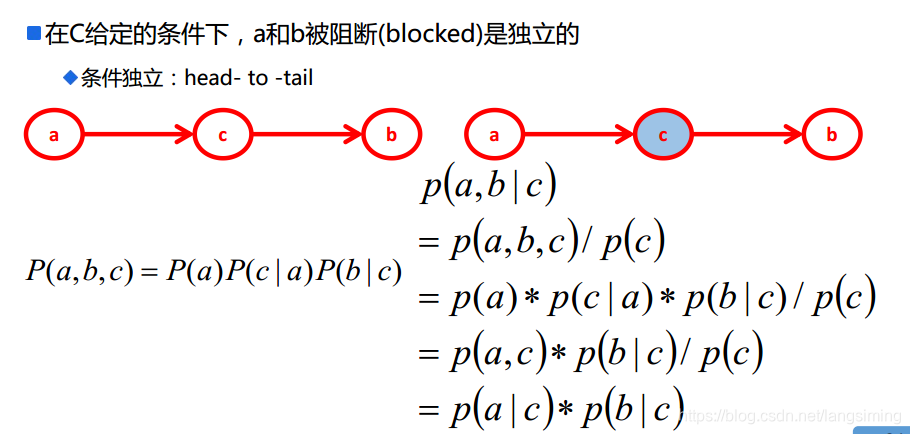
  贝叶斯网络判定条件独立-03