UnityShader入门精要_要点整理_数学篇

最新推荐文章于 2023-05-03 18:20:47 发布
原创 最新推荐文章于 2023-05-03 18:20:47 发布 · 387 阅读 · 4 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#shader

本文总结了学习Unity Shader所需的关键数学知识，包括坐标系、矩阵基础、几何变换矩阵等内容，并介绍了如何利用这些数学知识进行坐标空间变换及法线变换。

第四章介绍了诸多学习UnityShader需要的数学知识，这里总结一些个人认为比较重要的知识点，以便分享和后续查阅。

主要是回顾一下矩阵和然后记录坐标系转换方面的。

目录

左手坐标系，右手坐标系，左手法则右手法则？

矩阵基础概念

矩阵与矩阵的乘法

常见特殊矩阵概念

如何快速判断矩阵是正交的。

选择行矩阵还是列矩阵？

矩阵的几何性质

常见几何矩阵一览表

复合变换矩阵

给定一个复合旋转如何使用矩阵？

使用矩阵完成坐标空间(系)的变换

一个从模型到屏幕的完整标变换过程

为什要从观察空间（以相机为原点的空间）转换（投影）到裁剪空间？

观察空间到裁剪空间做了什么？

屏幕空间的变换是怎样的？什么是齐次除法？

从NDC在映射到真正的屏幕坐标。

法线变换

左手坐标系，右手坐标系，左手法则右手法则？

直接看图更清晰直观。

左手坐标系left_hand.png-40.5kB

右手坐标系right_hand.png-40kB

左右手法则分别对应，左手坐标系和右手坐标系中的旋转正方向。left_right_hand_rule.png-75.3kB

 

矩阵基础概念

矩阵与矩阵的乘法

书上概念：

 

演示计算步骤：

常见特殊矩阵概念

  • 矩阵的基础性质：
    • 矩阵乘法不满足交换律
    • 矩阵乘法满足结合律
  • 方块矩阵：行和列数量一样的就是方块矩阵，比如3*3，4*4的矩阵
  • 单位矩阵：一个任何矩阵和他相乘都是原来矩阵的矩阵。
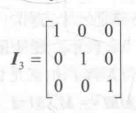
  • 转置矩阵：将原有的行换为列，将原有的列换为行，即为转置矩阵，表示为M^T。图为示例。

转置矩阵的性质一：转置矩阵的转置等于原矩阵

转置矩阵的性质二：矩阵串接的转置，等于反向串接各个矩阵的转置。

  • 逆矩阵：

逆矩阵的性质一：逆矩阵的逆矩阵是原矩阵的本身

逆矩阵的性质二：单位矩阵的逆矩阵是它本身

逆矩阵的性质三：转置矩阵的逆矩阵是逆矩阵的转置

逆矩阵的性质四：矩阵串接相乘后的逆矩阵等于反向串接各个矩阵的逆矩阵。

  • 正交矩阵：如果一个方阵M和他的转置矩阵的乘积是单位矩阵的话，我们就说这个矩阵是正交的。反过来说也是成立的。另外如果一个矩阵是正交的，那么他的转置矩阵和逆矩阵是相等的

如何快速判断矩阵是正交的。

选择行矩阵还是列矩阵？

如无特殊情况，Unity中使用列矩阵，和右乘。

矩阵的几何性质

常见几何矩阵一览表

 

平移矩阵：平移坐标点
 平移方向向量
缩放矩阵：一般缩放
 方向向量的缩放
旋转矩阵：绕X轴旋转θ的矩阵
 绕Y轴旋转θ的矩阵
 绕X轴旋转θ的矩阵


复合变换矩阵

绝大多多数情况下我们约定的顺序就是先缩放，再旋转，最后平移。（如果顺序不一致，得到变换矩阵将会不一样，但是书上没有给出明确的关系）。下图是只考虑Y轴旋转的复合变换的例子。

给定一个复合旋转如何使用矩阵？

假设绕X轴，Y轴，Z轴分别旋转θ角度。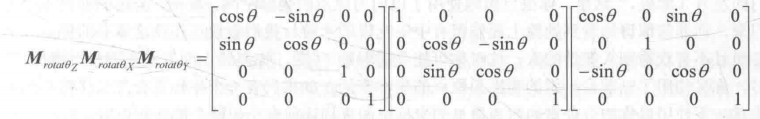要注意这个矩阵，对应的是每单次旋转后都更新旋转轴的情况，即下图。

使用矩阵完成坐标空间(系)的变换

假设我们要将坐标空间C转换到坐标空间P中，首先我们要知道坐标空间C在坐标空间P中的原点和坐标轴的矢量表示。然后把三个坐标轴依次放入矩阵的前三列。把原点放到最后一列。再用0和1填充最后一行即可。

如果我们只是变换方向矢量，可以只用一个3*3的矩阵，也就是前面的矩阵剔除掉平移的部分。

一个从模型到屏幕的完整标变换过程

首先是流程一览图。

vertex_conversion.png-100.9kBspace_handness.png-75.6kB

整个变换过程包含了比较多的的公式运算，这里节选比较重要的点做整理，（PS：主要整理透视投影）。

  • 为什要从观察空间（以相机为原点的空间）转换（投影）到裁剪空间？

    • 主要是常规的数学方法中，使用相机视锥体的6个面裁剪可视物体，比较麻烦，投影后可以使齐次坐标的w分量“有意义”，即，可以使用投影后生成齐次坐标的w分量，便捷的判断物体是否在视锥体范围内。更重要的是有了这个w分量，为了后续裁剪空间到屏幕空间的变换可以通过一个简单的“齐次除法”来完成。

  • 观察空间到裁剪空间做了什么？

首先是观察空间到裁剪空间的变换矩阵，该矩阵的推到过程可以看书上的流程，主要是使用相机的FOV和近裁剪面，远裁剪面进行一系列计算得出。

该矩阵表明了，整个投影过程实际上是对x，y，z分别作了不同程度的缩放，缩放的目的是为了方便裁剪。更重要的是，变换后的w分量，不再是1，而是原先z分量的取反结果。有了这个w分量后，我们可以通过如下不等式来判断，顶点是否在视锥体内。

以下是裁剪过程示意图。另外要注意的是，裁剪矩阵会改变空间的旋向性，也就是空间从右手坐标系变换到了左手坐标系，这意味着离相机越远，z值越大。

projection_matrix0.png-135.1kB

 

  • 屏幕空间的变换是怎样的？什么是齐次除法？

    齐次除法，简单来说就是使用坐标的xyz分量分别除以w分量，以得到一个在（0，1）范围内的归一化设备坐标（NDC）。

  • 从NDC在映射到真正的屏幕坐标。

    • 在Unity中，屏幕空间左下角的像素坐标是（0，0），右上角是（pixelWith，pixelHeight），而我们前面得到的NDC坐标x，y都是在[0，1]的范围内，所以要缩放到[0，pixelWith]，和[0，pixelHeight]范围，公式为另外，z轴坐标会直接除以w分量，然后把该值放到深度缓冲中去。

法线变换

法线变换的目标是，变换后仍然是跟切线垂直的一个方向向量。经过一堆推导得知，法线变换矩阵是原顶点变换矩阵的逆转置矩阵。

但是一般情况下，求解逆转置矩阵中的逆矩阵比较耗费运算量。我们可以通过两个特殊情况，避免解逆矩阵，获得法线变换矩阵。

  • 如果原变换矩阵只包含旋转，那么可以直接用原变换矩阵作为法线的变换矩阵。（PS：什么情况下只包含旋转呢）
  • 如果原变换矩阵只包含旋转和统一缩放，那么可以使用同一缩放系数来获得法线的变换矩阵，即
Unity+Shader入门精要-1. 入门shader
weixin_45218342的博客
04-29 1697
《Unity+Shader入门精要》的入门shader内容
Unity Shader入门精要——笔记
Andy Blog
07-23 1675
顶点数据–> 几何阶段：（顶点着色器–> 曲面细分着色器–>几何着色器–>裁剪–>屏幕映射）–>光栅化阶段（三角形设置–>三角形遍历–>片元着色器–>逐片元操作）–>屏幕图像顶点着色器：最基本的功能就是把模型的顶点坐标从模型空间转换到齐次裁剪坐标（通常串联成一个矩阵，即MVP矩阵）。
《UnityShader入门精要》UnityShader基础
qq_33187521的博客
09-23 457
UnityShader指的是一个ShaderLab文件——硬盘上以.shader作为文件后缀的文件 UnityShader对比传统shader的优缺点： （1）传统shader只能编写特定类型的shader，例如顶点着色器和片段着色器只能独立写在一份文件中，UnityShader可以在一个文件里写顶点着色器和片段着色器。 （2）传统shader无法在shader（顶点着色器，片段着色器）中设置一些渲染设置，例如是否开启混合，深度测试，模板测试等，需要在另外的代码中自行设置，UnityShader可以在sha
unity shader入门精要_零基础入门Unity Shader（一）
weixin_39917090的博客
12-06 364
本文转自Unity Connect博主 taecg前言Shader，中文名为着色器，对很多开发者来说它是一个神秘的存在，想学但是又不知道如何去学，或者学了一段时间发现Get不到它的点，始终感觉游离在外，无法开窍。那么本专栏（Unity技术美术）在前几篇介绍了美术资源标准后，打算接下来花一些篇章来讲下如何从零基础入门Shader，目的在于让初学Shader的程序或者美术可以快速进入这个丰富多彩的世界...
Unity Shader入门精要
Haipai1998的博客
06-19 6838
学习资料：Unity Shader入门精要 时长：一个月 计划：1~2天完成一章，预计一个月内完成 第二章 渲染流水线 性能瓶颈是消耗最大的流程 渲染流水线：应用阶段→几何阶段→光栅化阶段 应用阶段：CPU实现，输出渲染图元 数据加载到显存中:显卡对显存（VRAM）的访问速度比对内存（RAM）要快，并且大多数显卡对RAM没有访问权限 设置渲染状态：定义场景中的网格是怎样被渲染...
unity shader入门精要_Unity Shader 入门（二）：shader 基础
weixin_39989443的博客
12-15 572
一、参考与说明（需要写在开始东西）：1.1 Unity Shader 入门精要学习https://github.com/candycat1992/Unity_Shaders_Book/tree/unity_5_4​github.com1.2 写在开头，最近一直在关注渲染方面的文章，越看越发现，还是自下而上的学习路线比较好，了解背景原理，学习上层知识才更容易。但也确实发现，一头扎进去很容易迷茫，要学...
Unity_Shader高级篇_15_Unity Shader入门精要_水波效果
wy小骑士
04-04 2633
15.2 水波效果 在模拟实时水平的过程中，我们往往也会使用噪音纹理。此时，噪音纹理通常会用作一个高度图，以不断修改水面的法线方向。为了模拟水不断流动的效果，我们会使用和时间相关的变量来对噪声纹理进行采样，当得到法线信息后，再进行正常的反射+折射计算，得到最后的水面波动效果。 本节中，我们将会使用一个由噪声纹理得到的法线贴图，实现一个包含菲涅尔反射（10.1.5）的水面效果。如下图所示: ...
【Unity Shader入门精要_01】——坐标空间、坐标空间的变换
weixin_44794443的博客
03-29 644
数学原理在这 Note_3博客中。 文章目录常见的坐标空间类型模型空间世界空间观察空间裁剪空间屏幕空间坐标空间的变换 常见的坐标空间类型 模型空间 世界空间 观察空间 又称摄像机空间，是右手坐标系，即以摄像机为原心、x轴正方向在右边、y轴正方向在上方、摄像机朝向z轴负方向，这一点与前两个空间模型不同。但在学习过程中，可以简单理解左手空间和右手空间坐标系是镜像的，除了z轴不同，其余的坐标轴都相同。 但是在Unity中，直接调用类似Camera.cameraToWorldMatrix 、Camera..
Unity Shader 入门书籍高清完整版PDF
01-29
本书“Unity Shader入门书籍高清完整版PDF”为初学者提供了全面而深入的学习路径，帮助理解并掌握Shader编程的核心概念。 首先，Shader在Unity中的角色是解释如何在屏幕上绘制游戏物体。它们直接影响到游戏画面的...
渲染-光照模型03 高光反射模型实现
qq_40309483的博客
11-02 685
1.高光反射模型（Phong光照模型） 以下高光反射模型又被称为Phong光照模型 高光反射模型颜色=（入射光线颜色*材质高光反射系数）（max（0，视角方向 * 反射方向）^光滑程度） 其中， 反射方向=光源方向-2 （表面法线 * 光源方向） 表面法线 通常计算反射方向可以用内置函数reflect函数 2.高光反射模型的unityShader实现 与漫反射模型一样，实现方式同样有二，分别在顶点着色器和片元着色器中实现。 2.1在顶点着色器中实现 Shader "Unity Shaders Book/Ch
UnityShader入门精要-unity shader基础
weixin_58624886的博客
05-11 2036
Unity中的shader assets-create-shader创建，共有四个模板可供选择： standard surface shader 包含标准光照模型的表面着色器模板 unlit shader 不包含光照但包含雾效的基本顶点片元着色器 imageeffect shader实现屏幕后处理效果的基本模板 computeshader 旨在利用GPU并行性进行一些与常规渲染流水线无关的计算 Unity Shader 的结构 Properties属性 在properties中的定义会显示在
unity Shader 入门精要 EX
xinghaikongmeng的博客
10-19 4890
1、shader概念 Shader，中文名为着色器。 Shader其实就是专门用来渲染图形的一种技术，通过shader，我们可以自定义显卡渲染画面的算法，使画面达到我们想要的效果。 2、shader分类 Shader分为两类 ： 顶点Shader（3D图形都是由一个个三角面片组成的，顶点Shader就是计算每个三角面片上的顶点，并为最终像素渲染做准备）。 像素Shader，顾名思义，就是以像素为单位，计算光照、颜色的一系列算法。 几个不同的图形API都有各自的Shader语言 在DirectX中，顶点sha
Unity shader入门精要（学习总结）
Mq110m的博客
05-03 5059
shader 入门精要学习记录
【吴恩达机器学习笔记】第三章：线性回归回顾
weixin_42017042的博客
01-12 247
本章是对线性代数的一些简单回顾，由于之前学过，所以这里只是简单的将课程中的一些例子粘过来 矩阵表示 矩阵加法和标量乘法 矩阵向量乘法 用矩阵向量乘法来同时计算多个预测值 矩阵乘法 用矩阵乘法同时计算多个回归函数的多个预测值 矩阵乘法不满足交换律 矩阵乘法满足结合律 单位矩阵 矩阵的逆 矩阵的转置 ...
Unity Shader入门精要一
一条咸鱼的博客
08-15 975
1.渲染流水线 应用阶段——>几何阶段——>光栅化阶段 2.应用阶段分为三个阶段 （1）把数据加载到显存 （2）设置渲染状态 （3）调用DrawCall 3.几何阶段流水线 顶点数据——>顶点着色器——>曲面细分着色器——>几何着色器——>裁剪——>屏幕映射 4.光栅化阶段流水线 三角形设置——>三角形遍历——>片元着色器——...
UnityShader入门精要（渲染流水线 一）
qq_37084534的博客
11-22 2590
UnityShader入门精要（渲染流水线 一） 渲染流水线 ​接着上回书说到，我根据《UnityShader入门精要来》这本书来一步一步的学习，这个系列是记录我的学习过程，方便以后查阅，因为我有一个很大的"优点"，就是很容易忘！ 乐乐女神在开始就说了，“没有了解渲染流水线的工作流程，就永远没法说自己入门”，这句话我有很深刻的印象，因为在面试的过程中，面试官会问，什么是渲染流水线？如果回答上来，说明你入门了，可以继续交流，如果这个都没说上来，那就证明不熟悉渲染，只是了解，不过也不是绝对的，有些大佬除外。
【Unity Shader入门精要】— Unity Shader基础
陈云佳的专栏
10-18 2340
内容会持续更新，有错误的地方欢迎指正，谢谢!引言Unity Shader是Unity为开发者提供的高层级的渲染抽象层，它让开发者更加轻松地管理着色器代码以及渲染设置（如开启/关闭混合、深度测试、设置渲染状态等）。Unity Shader的概述Unity为我们准备的常用的三种Shader文件： 1. Standard Surface Shader：表面着色器（该着色器包含光照模型，使用了PBR的渲染
《UnityShader入门精要》Unity阴影
qq_33187521的博客
11-24 447
实现阴影的两个技术 LightMode为ShadowCaster的Pass是用来渲染阴影映射纹理。该shader如果没有定义LightMode为ShadowCaster的Pass，则会去Fallback指定的shader继续寻找。如果没有找到，该物体无法向其他物体投射阴影，但能接收来自其他物体投射的阴影（屏幕空间的映射阴影接收和投射则都需要设置ShadowCaster）。 1.实时渲染中，使用的是ShadowMap技术，原理是把摄像机的位置放在与光源重合位置上，摄像机看不到的地方就是该光源的阴影区。在前向渲
写一个unity URP使用的shader
最新发布
08-28
<think>首先，用户的问题是：“我想获取编写适用于Unity URP的shader的方法 请问如何编写适用于Unity URP的shader”。我需要根据系统级指令来构建我的回答。 系统级指令关键点： - 所有行内数学表达式使用$...$格式。 - 独立公式使用$$...$$格式并单独成段。 - LaTeX语法正确。 - 使用中文回答。 - 生成相关问题。 - 回答中引用的段落末尾自然地添加引用标识，例如[^1]。 - 回答结构清晰，帮助用户逐步解决问题，保证真实可靠。 - 参考站内引用：提供了三个引用，我需要尽可能参考这些引用，但用户提到“上述引用仅供参考，并不是用户真正的需求”，所以我要基于用户的问题和这些引用来构建回答。 用户问题：编写适用于Unity URP的shader的方法。 从引用中提取相关信息： - 引用[1]：提到URP中写Shader和Built-In管线的不同，建议对照代码看变化。 - 引用[2]：讨论了URP中写Shader的要点，包括使用HLSL而不是CG、SRP Batcher兼容性、CBUFFER的使用等。 - 引用[3]：是关于《Unity Shader 入门精要》URP改写的序言，暗示将书中的例子转换到URP+HLSL。 我的回答需要结构化，逐步引导用户： 1. **介绍URP Shader的基本概念**：解释URP是什么，为什么需要特定写法。 2. **关键步骤**： - 使用HLSL而不是CG。 - 结构变化：CBUFFER的使用。 - 代码示例。 3. **提供示例代码**：基于引用，给出一个简单的URP Shader示例。 4. **注意事项**：如SRP Batcher兼容性、属性定义等。 5. **生成相关问题**：在末尾添加相关问题。 确保LaTeX使用： - 用户问题中没有明显的数学表达式，但如果有涉及数学，如变量，使用$...$。例如，在解释Shader属性时，如果有数值范围，可以用$[0,1]$。 - 独立公式：如果讨论渲染方程之类，但这里可能不需要，所以保持简洁。 回答结构： 1. **开头**：简要回答用户问题。 2. **主体**：分步骤解释如何编写URP Shader。 - 步骤1: 理解URP Shader的结构。 - 步骤2: 使用HLSL语言。 - 步骤3: 定义属性和CBUFFER。 - 步骤4: 编写顶点和片段着色器。 - 步骤5: 示例代码。 3. **结尾**：总结和注意事项。 4. **相关问题**：生成3-5个相关问题。 引用标识： - 在回答中引用参考内容时，在末尾添加[^1]、[^2]等。例如，提到URP与Built-In的不同时，引用[^1]。 生成相关问题： - 基于用户问题，如URP Shader的优化、常见问题、升级指南等。 最终回答用中文。</think>以下是针对“如何编写适用于Unity URP的Shader”的详细解答。我将基于Unity URP（Universal Render Pipeline）的特性，结合关键步骤、代码示例和注意事项，逐步引导您完成。URP是Unity的高性能渲染管线，它使用HLSL语言（而非旧版CG）并优化了Shader结构以实现SRP Batcher兼容性[^1][^2]。回答参考了Unity官方文档和社区最佳实践，确保真实可靠。 ### 步骤1: 理解URP Shader的基本结构 URP Shader使用ShaderLab语法，但核心代码从CG迁移到HLSL。与旧版Built-In管线相比，主要变化包括： - **语言切换**：URP推荐使用HLSL（High-Level Shading Language），因为CG已停止更新，且HLSL支持SRP Batcher（提升渲染性能）[^2]。如果您使用CGPROGRAM块，Unity会自动引入内置库，可能导致冲突。 - **属性定义**：所有材质属性必须封装在`UnityPerMaterial` CBUFFER（常量缓冲区）中，以兼容SRP Batcher。这优化了GPU内存访问。 - **着色器块**：顶点和片段着色器代码需写在HLSLPROGRAM/ENDHLSL块内。 - **包含文件**：URP提供特定头文件（如`Packages/com.unity.render-pipelines.universal/ShaderLibrary/Core.hlsl`），简化光照和坐标转换。 ### 步骤2: 关键步骤详解 #### (1) 定义属性和CBUFFER 在Shader的Properties块声明属性（如颜色、纹理），然后在HLSL代码中用CBUFFER封装。例如，定义一个基础颜色属性： ```hlsl Properties { _BaseColor ("Base Color", Color) = (1,1,1,1) } HLSLPROGRAM // 必须将属性放入UnityPerMaterial CBUFFER CBUFFER_START(UnityPerMaterial) half4 _BaseColor; CBUFFER_END ``` - **为什么用CBUFFER**：SRP Batcher要求属性数据连续存储，否则会降级为传统渲染路径[^2]。 - 数学范围提示：颜色值通常在$[0,1]$区间，使用`half4`（半精度浮点数）节省内存。 #### (2) 编写顶点和片段着色器 URP着色器需包含顶点着色器（处理模型空间到裁剪空间转换）和片段着色器（计算像素颜色）。示例使用简单无光照（Unlit）模型： ```hlsl // 包含URP核心库 #include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/Core.hlsl" struct Attributes { float4 positionOS : POSITION; // 模型空间位置 }; struct Varyings { float4 positionCS : SV_POSITION; // 裁剪空间位置 }; Varyings vert(Attributes input) { Varyings output; // 转换到裁剪空间 output.positionCS = TransformObjectToHClip(input.positionOS.xyz); return output; } half4 frag(Varyings input) : SV_Target { // 直接返回基础颜色 return _BaseColor; } ``` - **坐标转换**：URP提供`TransformObjectToHClip`等函数，替代旧版`UnityObjectToClipPos`。 - **性能优化**：使用`half`代替`float`（精度要求不高时），减少GPU开销。 #### (3) 完整Shader示例 以下是一个简单的URP Unlit Shader，支持基础颜色输出： ```hlsl Shader "Example/URPUnlitShader" { Properties { _BaseColor ("Base Color", Color) = (1,1,1,1) } SubShader { Tags { "RenderType"="Opaque" "RenderPipeline"="UniversalPipeline" } Pass { HLSLPROGRAM #pragma vertex vert #pragma fragment frag #include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/Core.hlsl" CBUFFER_START(UnityPerMaterial) half4 _BaseColor; CBUFFER_END struct Attributes { float4 positionOS : POSITION; }; struct Varyings { float4 positionCS : SV_POSITION; }; Varyings vert(Attributes input) { Varyings output; output.positionCS = TransformObjectToHClip(input.positionOS.xyz); return output; } half4 frag(Varyings input) : SV_Target { return _BaseColor; } ENDHLSL } } } ``` - **测试方法**：在Unity中创建材质，应用此Shader，调整`_BaseColor`观察效果。 - **对比Built-In**：旧版Shader使用CGPROGRAM和`UnityObjectToClipPos`，URP改用HLSL和内置函数[^1]。 ### 步骤3: 注意事项和常见问题 - **SRP Batcher兼容性**：确保所有属性在`UnityPerMaterial` CBUFFER中，否则性能下降。检查方法：在Frame Debugger中查看"SRP Batcher"状态。 - **光照和阴影**：如需光照，包含`Lighting.hlsl`并使用URP的PBR（Physically Based Rendering）函数。例如： ```hlsl #include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/Lighting.hlsl" ``` - **升级旧Shader**：从Built-In迁移时： 1. 替换CGPROGRAM为HLSLPROGRAM。 2. 将属性移入CBUFFER。 3. 更新坐标转换函数（如`TransformWorldToHClip`）。 参考Unity官方升级手册[^2]。 - **错误处理**：常见错误包括未包含头文件或CBUFFER遗漏，Unity Editor控制台会提示具体信息。 ### 总结 编写URP Shader的核心是：使用HLSL语言、通过CBUFFER管理属性、并利用URP库函数简化开发。以上示例已覆盖基础流程，您可逐步扩展到复杂效果（如光照、透明）。实践中，建议对照URP官方示例（如Unlit Shader模板）调试[^1][^2]。 如果您有具体需求（如添加纹理或光照），请提供更多细节，我可以优化示例！
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值