SVD——奇异值分解概述

前言

奇异值分解（Singular Value Decomposition，简称 SVD)
奇异值分解是一个有着很明显的物理意义的一种方法，它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示，这些小矩阵描述的是矩阵的重要特性。
这是一个很著名的定理，广泛应用于图像压缩，矩阵填充，推荐系统和潜在语义索引（有时称为潜在语义分析）。
此文主要关注奇异值的一些特性，还会提及一些奇异值的计算以及相关的数学基础知识。之后还会涉及PCA。

特征值

特征值分解和奇异值分解两者有着很紧密的关系，特征值分解和奇异值分解的目的都是一样，即提取出一个矩阵最重要的特征。因此，首先从特征值分解讲起。(此部分主要参考资料1)
如果说一个向量$\nu$是方阵A的特征向量，则一定可以表示成下面的形式：
$$A\nu =\lambda \nu$$
其中$\lambda$被称为特征向量$\nu$对应的特征值，一个矩阵的一组特征向量为一组正交向量。计算特征值要求矩阵为方阵。

特征值分解则是将一个矩阵分解成下面的形式：
$$A=Q\sum Q^{-1}$$
这其中Q是这个矩阵A的特征向量组成的矩阵，$\sum$是一个对角矩阵，每一个对角线上的元素就是一个特征值。
一个矩阵其实就是一个线性变换，因为一个矩阵乘以一个向量后得到的向量，其实就相当于将这个向量进行了线性变换。从几何意义上来说，特征值和特征向量代表了主要方向及其大小。举一个具体的例子来说：

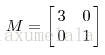
它对应的线性变换实际为下面的形式：

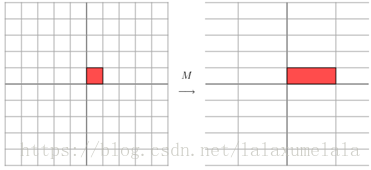
这是因为矩阵M乘以一个向量(x,y)的结果是：

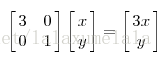
上面的矩阵是对称的，所以这个变换是一个对x，y轴的方向一个拉伸变换（每一个对角线上的元素将会对一个维度进行拉伸变换，当值>1时，是拉长，当值<1时时缩短），当矩阵不是对称的时候，假如说矩阵是下面的样子：

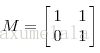
它所描述的变换是下面的样子：

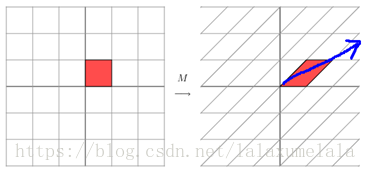
这其实是在平面上对一个轴进行的拉伸变换（如蓝色的箭头所示），在图中，蓝色的箭头是一个最主要的变化方向（变化方向可能有不止一个），如果我们想要描述好一个变换，那我们就描述好这个变换主要的变化方向就好了。反过头来看看之前特征值分解的式子，分解得到的Σ矩阵是一个对角阵，里面的特征值是由大到小排列的，这些特征值所对应的特征向量就是描述这个矩阵变化方向（从主要的变化到次要的变化排列）。
 

奇异值分解

特征值分解是一个提取矩阵特征很不错的方法，但是它只是对方阵而言的。那么如果A不是方阵，即行和列不相同时，我们还可以对矩阵进行分解吗？答案当然是可以，我们可以使用SVD。

奇异值分解：定义

奇异值分解是一个能适用于任意矩阵的一种分解方法。假设矩阵A是一个m$\times$n的矩阵，那么我们定义矩阵A的SVD为：
$$A=U\Sigma V^T$$
其中 U 是一个 m$\times$ m 的矩阵，U里面的向量称为左奇异向量，$\Sigma$ 是一个 m$\times$ n 的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值， V 是一个 n$\times$ n 的矩阵，V 里面的向量称为右奇异向量。 U 和 V 都是酉矩阵（正交矩阵），即满足$U^{T}U=I$, $V^{T}V=I$。下图可以很形象地看出上面SVD的定义：

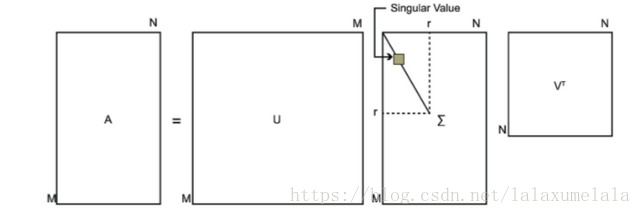
奇异值分解：求解过程

SVD分解后的U, $\Sigma$, V这三个矩阵的具体求解过程为：
首先，我们将A的转置和A做矩阵乘法，那么会得到 n$\times$ n 的矩阵的一个方阵$A^{T}A$。先对$A^{T}A$进行特征值分解：
（ A T A ） v i ⃗   =   λ v i ⃗ （A^T A）\vec {v_i} \ = \ \lambda \vec {v_i}