bzoj 1861: [Zjoi2006]Book 书架 (fhq_treap fa数组的应用）

题意

小T有一个很大的书柜。这个书柜的构造有些独特，即书柜里的书是从上至下堆放成一列。她用1到n的正整数给每本书都编了号。 小T在看书的时候，每次取出一本书，看完后放回书柜然后再拿下一本。由于这些书太有吸引力了，所以她看完后常常会忘记原来是放在书柜的什么位置。不过小T的记忆力是非常好的，所以每次放书的时候至少能够将那本书放在拿出来时的位置附近，比如说她拿的时候这本书上面有X本书，那么放回去时这本书上面就只可能有X-1、X或X+1本书。 当然也有特殊情况，比如在看书的时候突然电话响了或者有朋友来访。这时候粗心的小T会随手把书放在书柜里所有书的最上面或者最下面，然后转身离开。 久而久之，小T的书柜里的书的顺序就会越来越乱，找到特定的编号的书就变得越来越困难。于是她想请你帮她编写一个图书管理程序，处理她看书时的一些操作，以及回答她的两个提问：(1)编号为X的书在书柜的什么位置；(2)从上到下第i本书的编号是多少。

input

第一行有两个数n，m，分别表示书的个数以及命令的条数；第二行为n个正整数：第i个数表示初始时从上至下第i个位置放置的书的编号；第三行到m+2行，每行一条命令。命令有5种形式： 1． Top S——表示把编号为S的书房在最上面。 2． Bottom S——表示把编号为S的书房在最下面。 3． Insert S T——T∈{-1，0，1}，若编号为S的书上面有X本书，则这条命令表示把这本书放回去后它的上面有X+T本书； 4． Ask S——询问编号为S的书的上面目前有多少本书。 5． Query S——询问从上面数起的第S本书的编号。

output

对于每一条Ask或Query语句你应该输出一行，一个数，代表询问的答案。

思路

由于是序列的变化，要用序列平衡树，但是其中有些操作要查询 权值所在序列中的位置，也就是要在一颗序列树中找某个点的val=x，自顶向上肯定是不可以了。于是要记录每个节点的父亲，自下往上找到根为止，沿途记录符合答案的子树大小。
注意不能简单理解为该权值节点的左子树大小，因为其父亲的左子树都也可能满足条件。
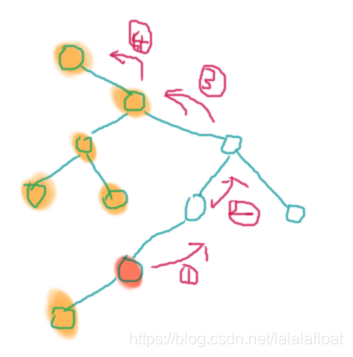
用 id[x] 记录权值 x 在树中节点的标号，注意在延 fa链往上找的过程中，只有在第一次向左拐之后（当前节点是父亲节点的右儿子之后）的所有节点都可以有贡献，res + = siz[ls[now]]+1；因为之前可能一直是一条左儿子的链，那么是不符号比 位置小于x 的。

如下图所示，若红色节点是目标点，容易看出黄色节点都是符合要求的位置小于其的节点，所以在图中第3步之后，才可以对途径节点进行个数统计。

代码

#include<bits/stdc++.h>
using namespace std;
#define maxn 300005
#define maxm 1006
#define ll long long int
#define INF 0x3f3f3f3f
#define inc(i,l,r) for(int i=l;i<=r;i++)
#define dec(i,r,l) for(int i=r;i>=l;i--)
#define mem(a) memset(a,0,sizeof(a))
#define sqr(x) (x*x)
#define inf (ll)2e18+1
#define PI acos(-1)
#define mod 10007
#define auto(i,x) for(int i=head[x];i;i=ed[i].nxt)
ll read(){
    ll x=0,f=1ll;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
     while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
     return f*x;
}
int n,m;
int val[maxn],rnd[maxn],siz[maxn],ls[maxn],rs[maxn],tot,rt,fa[maxn],id[maxn];
void pushup(int x){siz[x]=siz[ls[x]]+siz[rs[x]]+1; }
void split(int now,int k,int &x,int &y){
    if(!now){x=y=0;return ;}
    if(k<=siz[ls[now]]){
        y=now;
        split(ls[now],k,x,ls[now]);
        fa[ls[now]]=now;
    }
    else{
        x=now;
        split(rs[now],k-siz[ls[now]]-1,rs[now],y);
        fa[rs[now]]=now;
    }
    pushup(now);
}
void Merge(int &now,int x,int y){
    if(!x||!y){now=x+y;return ;}
    if(rnd[x]<rnd[y]){
        now=x;
        Merge(rs[now],rs[now],y);
        fa[rs[now]]=now;
    }
    else{
        now=y;
        Merge(ls[now],x,ls[now]);
        fa[ls[now]]=now;
    }
    pushup(now);
}
void inset(int va,int pos){
    int x=0,y=0,z=0;
    split(rt,pos-1,x,z);
    y=++tot;
    id[va]=y;val[y]=va;rnd[y]=rand();siz[y]=1;ls[y]=rs[y]=0;
    Merge(rt,x,y);
    Merge(rt,rt,z);
}
int query_val(int pos){
    int x=0,y=0,z=0;
    split(rt,pos,x,z);
    split(x,pos-1,x,y);
    int res=val[y];
    Merge(rt,x,y);
    Merge(rt,rt,z);
    return res;
}
int query_siz(int va){
    int res=siz[ls[id[va]]],now=fa[id[va]];
    bool flag=(rs[now]==id[va]);
    while(now){
        if(flag)res+=siz[ls[now]]+1;
        if(fa[now])flag=(rs[fa[now]]==now);
        now=fa[now];
    }
    return res;
}
void del(int va){
    int x=0,y=0,z=0;
    int pos=query_siz(va);
    split(rt,pos+1,x,z);
    split(x,pos,x,y);
    Merge(rt,x,z);
}
/*void dfs(int x){
    if(val[x]==0){printf("*\n");return ; }
    printf("val = %d    siz = %d\n",val[x],siz[x]);
    dfs(ls[x]);
    dfs(rs[x]);
    printf("val = %d    siz = %d\n",val[x],siz[x]);
}*/
int main()
{
    n=read();m=read();
    char s[10];int x,y;
    inc(i,1,n){
        x=read();
        inset(x,i);
    }
    inc(i,1,m){
        scanf("%s",s);
        if(s[0]=='T'){
            x=read();
            del(x);
            inset(x,1);
        }
        else if(s[0]=='B'){
            x=read();
            del(x);
            inset(x,n);
        }
        else if(s[0]=='I'){
            x=read();y=read();
            int pos=query_siz(x)+1;
            del(x);inset(x,pos+y);
        }
        else if(s[0]=='A'){
            x=read();
            printf("%d\n",query_siz(x));
        }
        else if(s[0]=='Q'){
            x=read();
            printf("%d\n",query_val(x));
        }
        //dfs(rt);
    }
    return 0;
}