acwing--126. 最大的和（dp）-优快云博客

该博客介绍了如何使用动态规划解决二维数组中求最大子矩阵和的问题。通过将二维数组转化为一维，利用前缀和技巧降低时间复杂度至O(n^3)，并给出了详细的C++代码实现。此算法适用于处理大规模数据，提高效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

ACWing最大的和

题目大意：求子矩阵的最大和

思路：在对二维求子矩阵，枚举复杂度为O(n^4)；

我们先从一维思考，如何求一维数组最大子串的和；

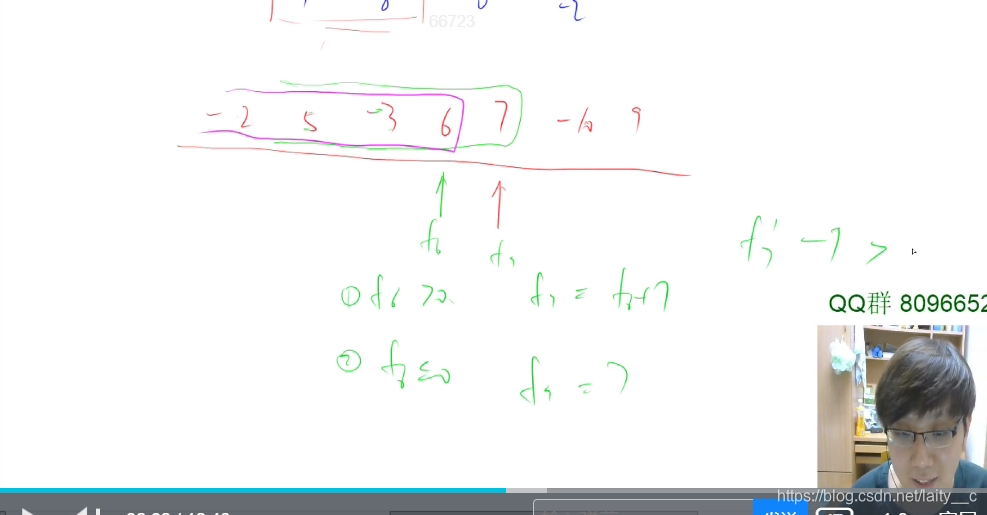
在这里插入图片描述

采用dp思路

dp[i]={ if(dp[i-1]<0,dp[i]=cnt[i]),

else(dp[i]=dp[i]+dp[i+1] );

这时候我们就很好理解将二维转变为了一维，此时我们再将每列当作一个元素，对存入数据求前缀和，将二维转变为一维，复杂度便是O(n^3)；只需对每列枚举它的起始点即可；

#include<bits/stdc++.h>
using namespace std;
int cnt[105][105];
int main(){
	int n;
	scanf("%d",&n);
	memset(cnt,0,sizeof(cnt));
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			cin >> cnt[i][j];
			cnt[i][j]+=cnt[i-1][j];//求前缀将其转为一维 
		}
	}
	
	int dp[105]={0};
	int res=-1e4;
	for(int i=1;i<=n;i++){//循环每行 
		for(int j=i;j<=n;j++){//前缀和的值cnt[j][k]-cnt[i-1][k]就是每列i-j相加的值 
			
			for(int k=1;k<=n;k++){
				if(dp[k-1]<0) dp[k]=cnt[j][k]-cnt[i-1][k];
				else dp[k]=cnt[j][k]-cnt[i-1][k]+dp[k-1];
				res=max(res,dp[k]);	
			}
			
		}
	} 
	
	cout << res << endl;
	return 0;
}