高级数据结构：并查集

最新推荐文章于 2022-07-17 14:25:54 发布

原创最新推荐文章于 2022-07-17 14:25:54 发布 · 266 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #算法 #c++ #并查集

算法模板专栏收录该内容

36 篇文章

订阅专栏

本文介绍了C++实现并查集的基本操作及优化，包括路径压缩和按秩合并，达到近乎常数时间复杂度。并展示了并查集在解决实际问题中的应用，如格子游戏、搭配购买、程序自动分析、奇偶游戏和银河英雄传说等题目，通过实例解析了如何运用并查集解决01背包、路径连接、集合合并与查询、异或游戏和势力范围合并等问题。

文章目录

#写在前面

#写在前面

基础并查集实现了

合并两个集合
查询某个元素的祖宗节点

基本优化

路径压缩 O(logn)
按秩合并
主要思想是合并集合时每次把树的深度较小的一个合并到深度较大的那一个
代码比较长 O(logn)

两个一起可以做到 O(α(n)) 反阿克曼函数
-阿克曼函数
阿克曼函数增长很快，反阿克曼函数增长很慢
基本看成 O(1) 的

并查集扩展

记录一下每个集合的大小，将集合大小这个属性绑定到根节点上
记录一下每个点到根节点的距离，这里需要绑定到每个元素身上，这个可以处理元素和根节点的关系，可以做多分类问题

##格子游戏

https://www.acwing.com/problem/content/1252/

问第一次形成环是什么时候

当要连的点已经在一个集合里则会出现环

细节问题：
二维矩阵转化成一维坐标
$(x, y) = > x * n + y$
前提是xy都从0开始
$(x, y) = > (x - 1) * n + (y - 1)$
从x=1,y=1开始

裸的并查集+坐标映射

----c++版

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;

const int N=45010;
int n,m;
int p[N];

int find(int x){
    if(p[x]!=x)p[x]=find(p[x]); // 这个写法有染色的功能
    return p[x];
}

int get(int x, int y){
    return (x-1)*n+(y-1);
}

int main(){
    cin>>n>>m;
    
    for(int i=0;i<=n*n;i++)p[i]=i;
    
    int res=0;
    for(int i=1; i<=m; i++){
        int x,y;
        char d;
        cin>>x>>y>>d;
       
        int a=get(x,y), b;
        if(d=='D')b=get(x+1, y);
        else b=get(x, y+1);
        
        int pa=find(a), pb=find(b);
        if(pa==pb){
            res=i;
            break;
        }
        p[pa]=pb;
    }
    if(!res)puts("draw");
    else cout<<res<<endl;
    
    return 0;
}

##搭配购买

https://www.acwing.com/problem/content/1254/

01背包+并查集

----c++版

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=10100;
int n,m, vol;
int v[N], w[N];
int p[N];
int f[N];

int find(int x){
    if(p[x]!=x)p[x]=find(p[x]);
    return p[x];
}

int main(){
    cin>>n>>m>>vol;
    for(int i=1; i<=n; i++)p[i]=i;
    for(int i=1; i<=n; i++)cin>>v[i]>>w[i];
    while(m--){
        int a,b;
        cin>>a>>b;
        int pa=find(a), pb=find(b);
        if(pa!=pb){
            v[pb]+=v[pa];
            w[pb]+=w[pa];
            p[pa]=p[pb];
        }
    }
    
    //01背包
    for(int i=1;i<=n; i++)
        if(p[i]==i)
            for(int j=vol; j>=v[i]; j--)
                f[j]=max(f[j], f[j-v[i]]+w[i]);
    
    cout<<f[vol]<<endl;
    return 0;
}

##程序自动分析

https://www.acwing.com/problem/content/239/

在这里插入图片描述

----c++版

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<unordered_map>
using namespace std;

const int N=2000010;

int n,m;
int p[N];
unordered_map<int, int> S;

struct Query{
    int x,y,e;
}query[N];

int get(int x){
    if(S.count(x)==0)S[x]=++n;
    return S[x];
}

int find(int x){
    if(p[x]!=x) p[x] =find(p[x]);
    return p[x];
}

int main(){
    int T;
    scanf("%d", &T);
    while(T--){
        n=0;
        S.clear();
        scanf("%d", &m);
        for(int i=0; i<m; i++){
            int x,y,e;
            scanf("%d%d%d", &x,&y,&e);
            query[i]={get(x), get(y), e};
            
        }
        
        for(int i=1; i<=n; i++)p[i]=i;
        //合并相等条件
        for(int i=0; i<m; i++)
            if(query[i].e==1){
                int pa=find(query[i].x), pb=find(query[i].y);
                p[pa]=pb;
            }
        //检查不等条件
        bool has_conflict=false;
        for(int i=0; i<m; i++)
            if(query[i].e==0){
                int pa=find(query[i].x), pb=find(query[i].y);
                if(pa==pb){
                    has_conflict=true;
                    break;
                }
            }
            
        if(has_conflict)puts("NO");
        else puts("YES");
    }
    return 0;
}

##奇偶游戏

https://www.acwing.com/problem/content/241/

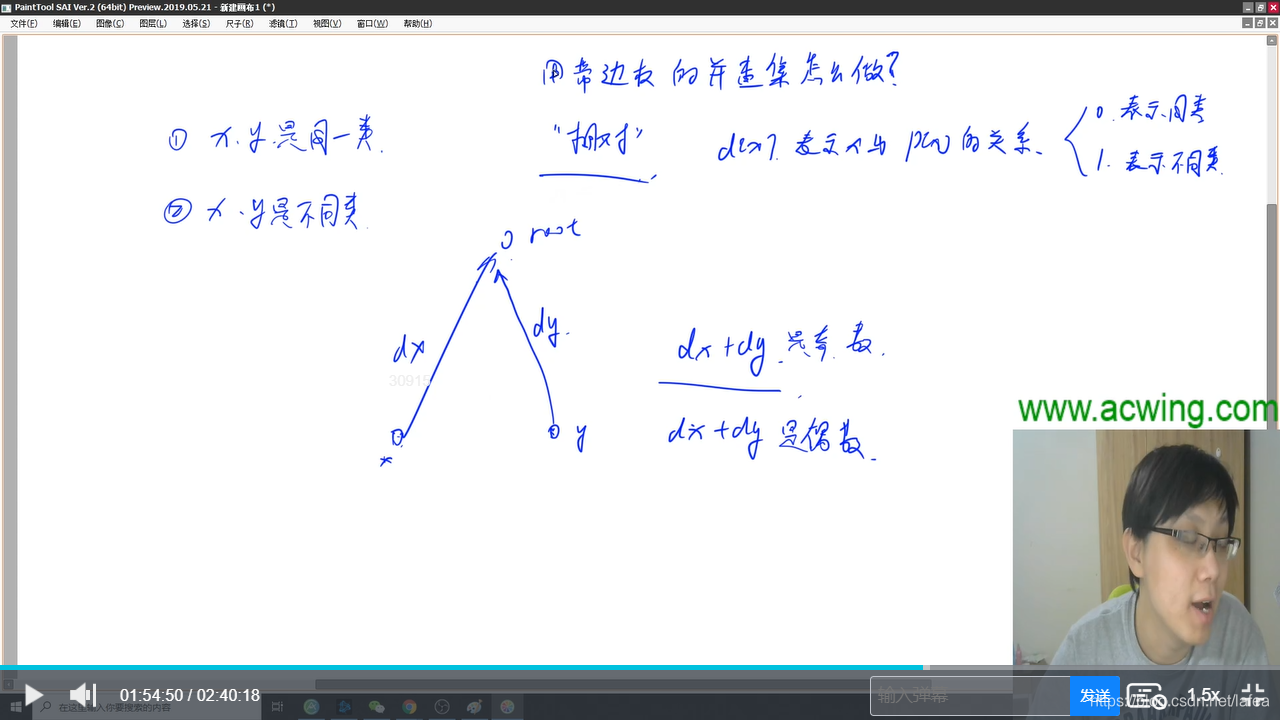
在这里插入图片描述

----c++版带权并查集

在这里插入图片描述

画出来的并查集大概是这样

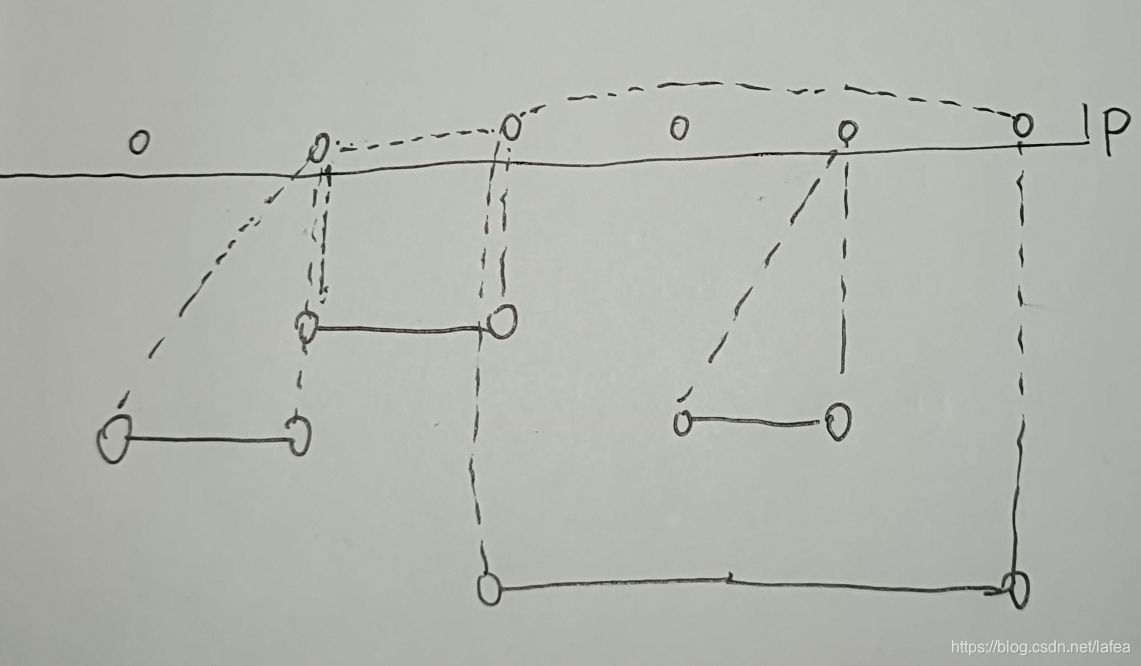
事实上，经过以上分析，序列的长度已经不重要了，主要是两个端点的奇偶性，只要满足，一定可以构造出这个01序列

这个并查集利用了存节点与根节点的关系，以及传递性(知道两个节点与根节点的关系，即可知道两个节点间的关系)

#include<iostream>
#include<algorithm>
#include<cstring>
#include<unordered_map>
using namespace std;
//序列长10^9, 离散化
//加法在模2的意义下是异或运算
const int N=20010;

int n,m, nn;
unordered_map<int, int> S;
int p[N], d[N];

int get(int x){
    if(S.count(x)==0)S[x]=++n;
    return S[x];
}

int find(int x){
    if(p[x]!=x){
        int root=find(p[x]);
        d[x]^=d[p[x]];
        p[x]=root;
    }
    return p[x];
}

int main(){
    cin>>nn>>m;
    n=0;
    int res=m;
    
    for(int i=0; i<N; i++)p[i]=i;
    
    for(int i=1;i<=m; i++){
        int a,b;
        string type;
        cin>>a>>b>>type;
        a=get(a-1), b=get(b);
        
        int t=0;
        if(type=="odd")t=1;
        
        int pa=find(a), pb=find(b);
        if(pa==pb){
            if((d[a]^d[b])!=t){
                res=i-1;
                break;
            }
        }else{
            p[pa]=pb;
            d[pa]=d[a]^d[b]^t;
        }
    }
    
    cout<<res;
    return 0;
}

----c++版拆点并查集（邻域并查集）

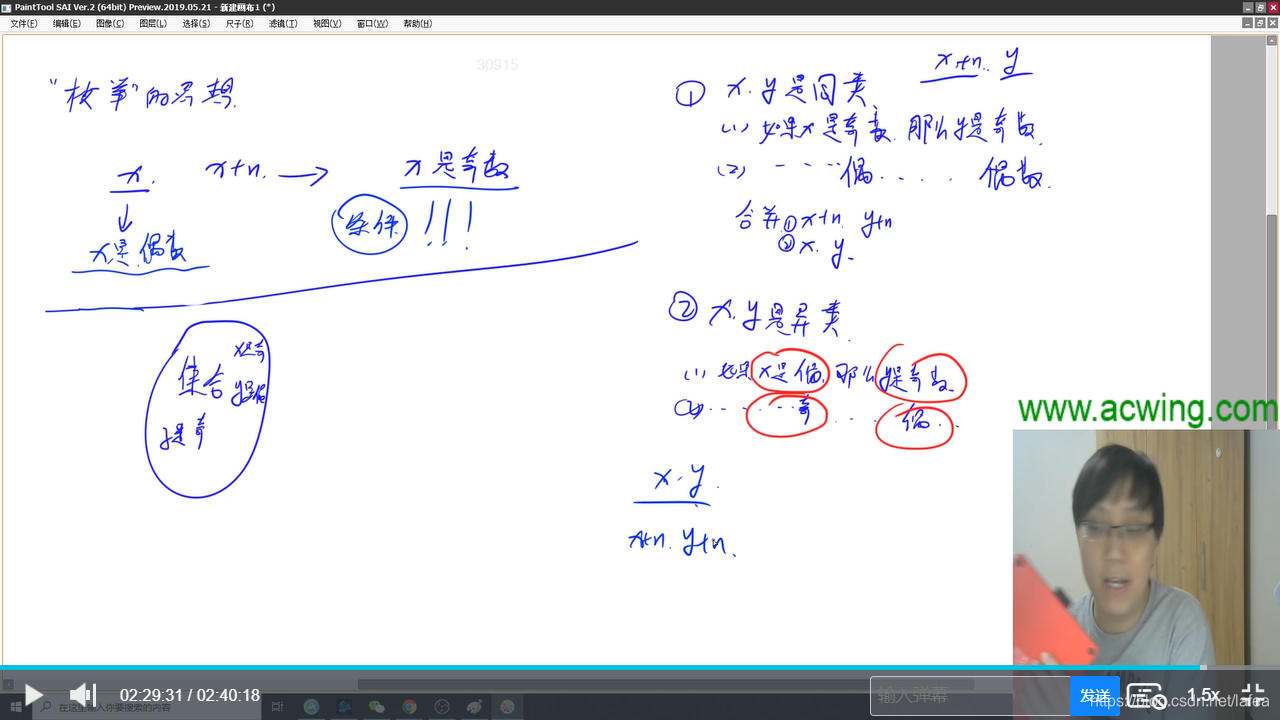
在这里插入图片描述

#include<iostream>
#include<algorithm>
#include<cstring>
#include<unordered_map>
using namespace std;
//序列长10^9, 离散化
//加法在模2的意义下是异或运算
const int N=20010, Base=N/2;

int n,m, nn;
unordered_map<int, int> S;
int p[N], d[N];

int get(int x){
    if(S.count(x)==0)S[x]=++nn;
    return S[x];
}

int find(int x){
    if(p[x]!=x)p[x]=find(p[x]);
    return p[x];
}

int main(){
    cin>>n>>m;
    int res=m;
    nn=0;
    for(int i=0; i<N; i++)p[i]=i;
    
    for(int i=1;i<=m; i++){
        int a,b;
        string type;
        cin>>a>>b>>type;
        a=get(a-1), b=get(b);
        
        if(type=="even"){
            if(find(a+Base)==find(b)){// 只用判断一个就得了，因为合并时是双向的
                res=i-1;
                break;
            }
            p[find(a)]=find(b);
            p[find(a+Base)]=find(b+Base);
        }else{
            if(find(a)==find(b)){
                res=i-1;
                break;
            }
            p[find(a+Base)]=find(b);
            p[find(a)]=find(b+Base);
        }
        
        
    }
    
    cout<<res;
    return 0;
}

##银河英雄传说

https://www.acwing.com/problem/content/240/

在这里插入图片描述

----c++版

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
const int N=30010;
int m;
int p[N], s[N], d[N];

int find(int x){ // find同时维护d  秀啊
    if(p[x]!=x){
        int root=find(p[x]);
        d[x]+=d[p[x]];
        p[x]=root;
    }
    return p[x];
}

int main(){
    scanf("%d", &m);
    for(int i=1; i<N; i++){
        p[i]=i;
        s[i]=1;
    }
    
    while(m--){
        char op[2];
        int a,b;
        scanf("%s%d%d", op, &a, &b);
        if(op[0]=='M'){
            int pa=find(a), pb=find(b);
            d[pa]=s[pb];
            s[pb]+=s[pa];
            p[pa]=pb;
        }
        else{
            int pa=find(a), pb=find(b);
            if(pa!=pb)puts("-1");
            else printf("%d\n", max(0, abs(d[a]-d[b])-1));
        }
    }
    return 0;
}