前言
相信不少码友都做过力扣hot100里的42. 接雨水,我个人的思路是从行的角度来看,下面我将结合图画推演和代码来简单的演示一下。
代码展示
class Solution {
public:
int trap(vector<int>& height) {
int n = height.size(); // 获取数组长度(柱子数量)
if (n <= 2) return 0; // 边界条件:少于3个柱子无法接水,直接返回0
int left = 0, right = n - 1; // 双指针:left从左向右,right从右向左
int rain = 0; // 存储总接水量
// 跳过左侧高度为0的柱子(这些柱子无法参与储水,不是有效边界)
while (height[left] == 0 && left < n) left++;
// 跳过右侧高度为0的柱子(同理,不是有效边界)
while (height[right] == 0 && right > 0) right--;
// 双指针遍历,直到左右指针相遇(所有区间处理完毕)
while (left < right) {
// 当前区间的有效储水高度由左右边界中较矮的那个决定(短板效应)
int h = min(height[left], height[right]);
// 计算当前区间(left到right)在高度h下的总面积(假设区间内全是水)
int s = h * (right - left + 1);
// 计算区间内柱子本身占据的面积(这些部分无法储水)
int unrain = 0;
for (int i = left; i <= right; i++) {
if (height[i] > h) {
// 柱子高度超过h,超出部分不影响储水,仅计算h高度内的柱子面积
unrain += h;
} else {
//柱子高度低于或等于h,直接累加其高度,同时将其"补高"到h(标记已统计的雨水)
unrain += height[i];
height[i] = h;
}
}
// 当前区间的储水量 = 总面积 - 柱子占据的面积,累加到总接水量
rain += s - unrain;
// 移动指针到下一个有效边界(寻找比当前h更高的柱子,作为新的边界)
if (height[left] <= height[right]) {
// 左边界较矮,移动左指针到第一个比h高的柱子(新的左边界)
while (height[left] <= h && left < right) left++;
} else {
// 右边界较矮,移动右指针到第一个比h高的柱子(新的右边界)
while (height[right] <= h && left < right) right--;
}
}
return rain; // 返回总接水量
}
};思路讲解
看到这题,我的第一想法是定义左指针 left 和右指针 right ,从数组两端第一个非零点(0的话存不了水,所以可以直接跳过)开始遍历,每次计算左右指针能装下最大水量的面积 s,然后遍历左右指针区间,计算不能存水的面积 unrain,就可以得到该 h 行能存放的雨水 rain 。
之后移动左右指针较小的一个,为什么不移动大的那个呢?
其实,这题的关键就在这里,小的那边能存放的雨水已经被统计完了(比如图例第一次,第一行能存的雨水都被统计完了),而较大的那边后续可能有比它更大的(比如图例第二次,第二行的还没统计),为了避免漏算,所以要保留较大的。

第一次时,left=1,right=11,height[left]=1,height[right]=1,高度h为1 ( min(height[left], height[right]) ),所以此时s=1*(11-1+1),unrain=9,rain=s-unrain=2。
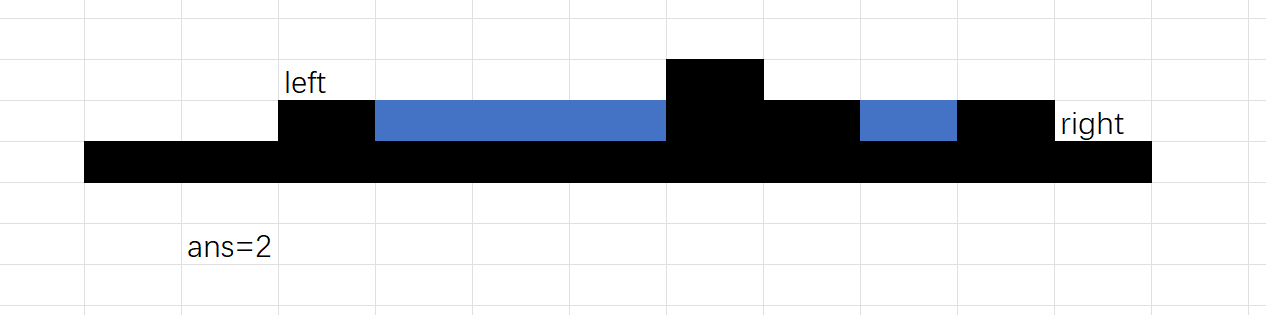
之后把第一行全部标记为黑,移动left,此时height[left]=0小于h,所以继续移动,此时height[left]=2,又因为height[right]=1,根据水桶效应,还是计算h=1的(已经计算过了),跳过。
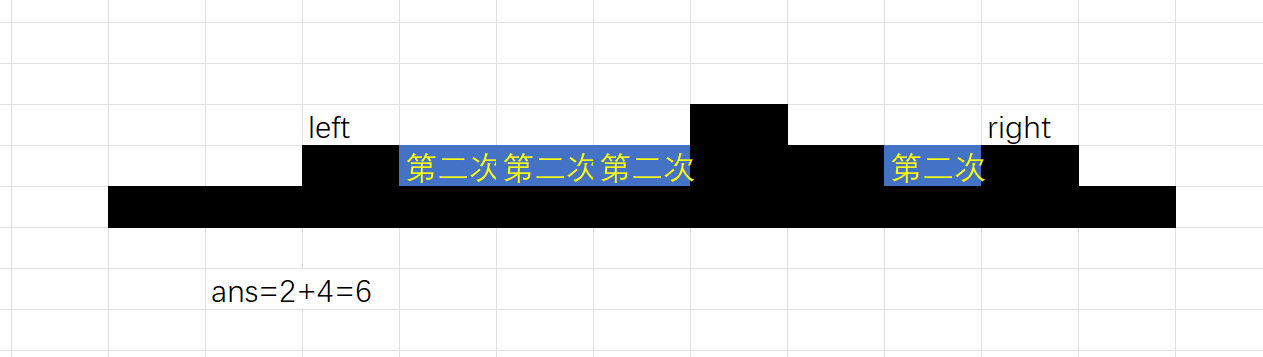
移动right,此时height[left]=2,此时h=2,s=2*(10-3+1)=16,unrain=12,rain=2+(16-12)=6
以上便是演示结果,有不当之处,还请大神指正。





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








