基于Pytorch 实现残差网络ResNet

基于Pytorch 实现残差网络ResNet

（一）残差？

“数理统计中残差是指实际观察值与估计值（拟合值）之间的差。如果回归模型正确的话， 可以将残差看作误差的观测值。”

“统计学上把数据点与它在回归直线上相应位置的差异称残差”

简单地说，已知函数f(x),想得到f(x0)=b时x0的取值，x0未知，给定一个x0的估计值x1，可以根据b-f(x1)可以求得残差。（与误差x1-x0区别：可以在x0未知的情况下取得)

（二）残差网络

1）Idea起源：

神经网络随着层数的增加可能会出现两个问题：精度下降问题 和 梯度消失/爆炸问题。

2)Idea: 引入恒等映射

恒等映射（Identity Mapping）:对任意集合A，如果将映射f : A → A 定义为f ( x ) = x ，即规定A中每个元素x 与自身对应，则称f 为A上的恒等映射

在极端情况下，如果一个恒等映射是最优的，那么将残差置为零比通过一堆非线性层来拟合恒等映射更容易。快捷连接简单地执行恒等映射，并将其输出添加到堆叠层的输出（图2）。恒等快捷连接既不增加额外的参数也不增加计算复杂度。整个网络仍然可以由带有反向传播的SGD进行端到端的训练。

原始网络： 输入： x                        输出：权重w'和x的关系函数       目标：F(x,w')->目标函数H(x)

残差网络： 输入：又添加了一个 x   输出:   F(x)+x                             目标： F(x,w)+x ->目标函数H(x) 即F(x,w)->H(x)-x  (如果F(x,w)权重都为零，即为恒等映射）

3）残差网络结构

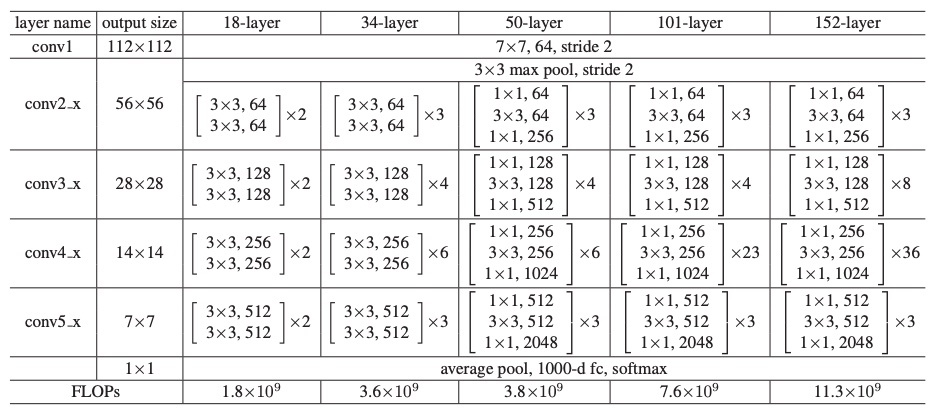
作者提出的残差块有两种结构(左图：对应Res-18/34  右图：对应Res-54/101/152)：

4) 残差网络逐步实现（ResNet-18 和 ResNet-54）

ResNet-18

ResNet-18分为6个部分：

1. Conv1：第一层卷积，没有shortcut机制。
2. layer1：第一个残差块，一共有2个。(每个Layer由若干个Block组成)
3. layer2：第二个残差块，一共有2个。
4. layer3：第三个残差块，一共有2个。
5. layer4：第四个残差块，一共有2个。
6. fc：全连阶层。

PS:这里的残差块是：BasicBlock(区别于后面ResNet中用到的Bottleneck)

1  Conv1

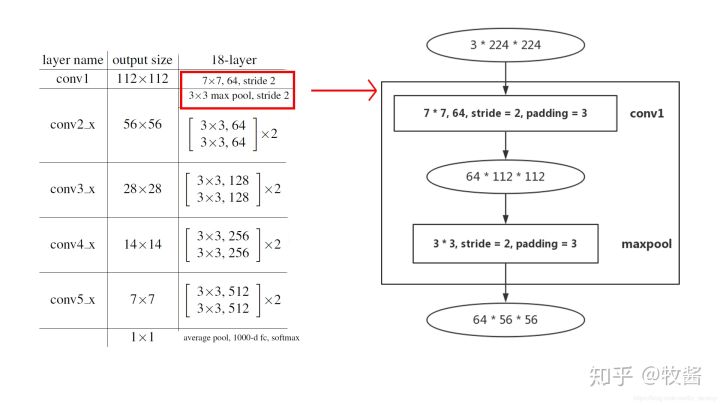
输入输出用椭圆形表示，中间是输入输出的尺寸：channel×height×width

直角矩形框指的是卷积层或pooling层，如“3×3,64,stride=2,padding=3 3 \times 3, 64, stride = 2, padding = 33×3,64,stride=2,padding=3”指该卷积层kernel size为3×3 3 \times 33×3，输出channel数为64，步长为2，padding为3。矩形框代表的层种类在方框右侧标注，如“conv1”。

卷积层的输出尺寸计算公式：

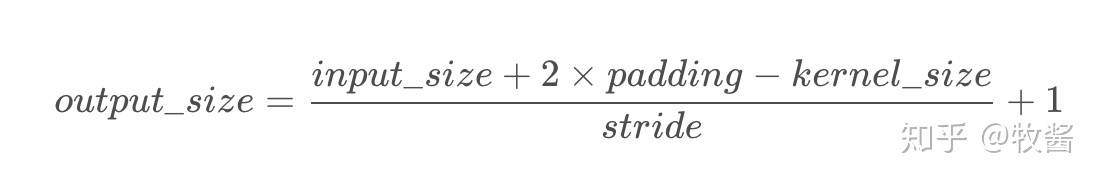
2 Layer1

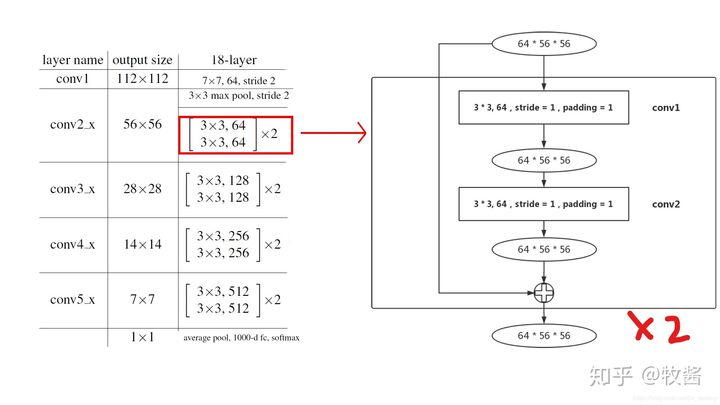
layer1的结构中没有downsample。右图是BasicBlock的主要结构——两个3×3 卷积层。Layer1由两个Block组成（左图中×2） ，即 两个右图结构重复连接。

2 Layer2

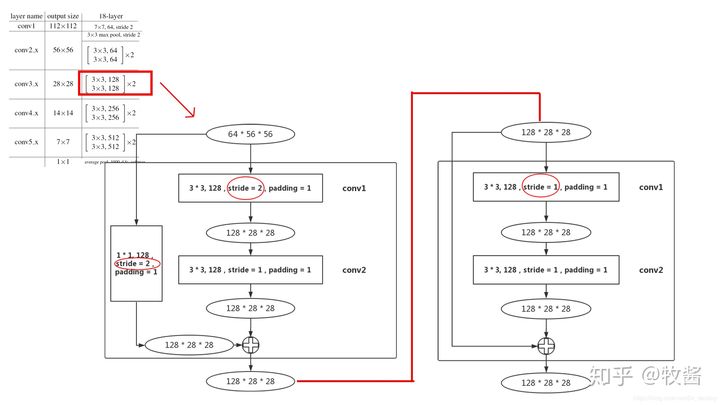
layer2:

首先64×56×56输入进入第1个block的conv1，这个conv1的stride变为2，和layer1不同（图红圈标注），这是为了降低输入尺寸，减少数据量，输出尺寸为128×28×28 。

最后到第1个block的末尾处，需要在output加上residual，但是输入的尺寸为64×56×56 ，所以在输入和输出之间加一个 1×1 卷积层，stride=2（图红圈标注），作用是使输入和输出尺寸统一（该部分即：PyTorch ResNet代码中的downsample）。由于已经降低了尺寸，连接的第2个block的conv1的stride就设置为1。由于该block没有降低尺寸，residual和输出尺寸相同，所以也没有downsample部分。

3 layer3-4

layer3和layer4结构和layer2相同，只是通道数变多，输出尺寸变小。

ResNet18和34都是基于Basicblock，结构非常相似，差别只在于每个layer的block数。

Pytorch实现ResNet-18

import torch
import torch.nn as nn
import torch.nn.functionl as F

#定义残差块ResBlock
class ResBlock(nn.Module):
    def __init__(self, inchannel, outchannel, stride=1):
        super(ResBlock, self).__init__()
        #残差块内连续的2个卷积层
        self.left = nn.Sequential(
            nn.Conv2d(inchannel, outchannel, kernel_size=3, stride=stride, padding=1, bias=False),
            nn.BatchNorm2d(outchannel),
            nn.ReLU(inplace=True),
            nn.Conv2d(outchannel, outchannel, kernel_size=3, stride=1, padding=1, bias=False),
            nn.BatchNorm2d(outchannel)
        )
        self.shortcut = nn.Sequential()
        if stride != 1 or inchannel != outchannel:
            #shortcut，这里为了跟2个卷积层的结果结构一致，要做处理
            self.shortcut = nn.Sequential(
                nn.Conv2d(inchannel, outchannel, kern