MFC 2010 C++ A*寻路算法

最新推荐文章于 2025-04-14 11:09:55 发布
最新推荐文章于 2025-04-14 11:09:55 发布
阅读量1.3k 收藏 17
点赞数 6
分类专栏： C/C++
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/l198738655/article/details/80242180
版权
本文详细介绍了一种广泛应用于游戏开发中的A*寻路算法，包括算法的基本原理、实现步骤及注意事项。通过C++实现A*算法，并展示了如何在游戏地图中寻找最优路径。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >


     因为要开发游戏辅助需要解决寻路问题，当然游戏辅助寻路有很多种方式，比如定点寻路就是预先设定几个坐标点，只要保证点与点之间的直线没有障碍物就能像火车一样一站一站的跑下去。对于经过游戏中的大地图，比如由A点的某个NPC处拿个物品交给大地图另一头的某个NPC就比较适合用这种定点寻路的方式，这种方式简单粗暴，比较有效率。缺点是如果半路有个怪什么的打你一拳，可能就会偏离预定路线，而找不到回家的路。此时就可以结合A*算法收拾了干扰我们维护世界和平的渣茬后自动规划路线回到离人物最近的那个点，继续沿着路线走路。A*算法的一个问题就是容易贴着墙走特别是通道比较“粗”的时候，但如果给A*算法加上其他的判断条件来优化寻路逻辑又会增大每一步判断时的运算量，虽然基础的A*算法有贴着墙走的毛病，但却是一个运算量和运算结果比较平衡的一个选择。


首先介绍A*算法的运行逻辑

 



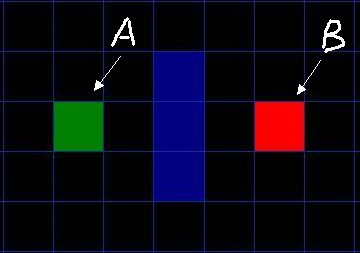
     如图所示简易地图, 其中绿色方块的是起点 (用 A 表示), 中间蓝色的是障碍物, 红色的方块 (用 B 表示) 是目的地. 为了可以用一个二维数组来表示地图, 我们将地图划分成一个个的小方块。

 

 

 

 

既然是用C++来编写当然要用到STL标准模板库，STL提供了几种容器类型，这里使用list容器来实现。

开始寻路：

首先设置4个列表

开启列表

关闭列表 --关闭列表都是检测过的方格

考察列表

结果列表  --存放着已经确定的最终路径，最后就要沿着这个路径走路


1.首先遍历起始点周围的8个格子，找出所有能通行的格子，分别计算它们的F H G值，放入结构体，再把结构体放入开启列表中。

 

 

 

 

 

 

 

 

     list容器提供了一个sort()方法，sort()方法又有一个重载版本，允许我们自定义一个函数来规定排序逻辑，因此我们可以指定sort()方法按照结构体内的某个变量来进行排序，在这里我们当然按照F值大小来进行排序，对比前后两个list元素的F值大小来进行排序。完成一次排序后，开启列表第一位的元素就是F值最小的那个格子了。


在这里需要说明一下F H G值分别代表什么，以及如何算出。

H


H值代表某个格子与终点的距离，或者也可以理解为移动到终点所需要花费的代价。H值有多种方法计算，比较常见的算法为曼哈顿算法和欧几里得算法，欧几里得算法其实就是勾股定理，计算的是某点与终点的直线距离；而曼哈顿算法则更简单粗暴一些，是用某点的X坐标减去终点X坐标，Y坐标减去终点Y坐标，最后取绝对值，然后把两个绝对值X Y相加就得到H值了。本例用的是曼哈顿算法。

G


G值就是当前格子移动到周围格子的路程（代价），比如说直着走肯定比斜着走路程短，经过业界大神夜以继日不眠不休的论证之后决定把直着的路程定义为10，斜着走的路程定义为14。

F

 

 

 

F值就是以上两个值G+H之和，反应了一个格子的总性价比。然后我们就依靠这个性价比来判断走这个格子划算还是走那个格子划算。


2.把起点放入关闭列表中，以免再次检测。

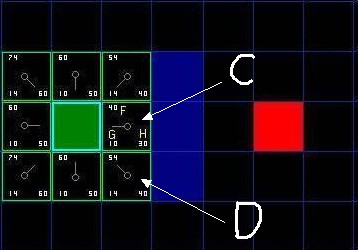
3.然后每个格子都有了自己的 F H G值，如下图，选择一个F值最小的，在图中是C方格，把它放进考察结构体中，然后遍历考察结构体周围的8个方格。放入考察列表中，排序后再次选出F值最小的那个格子。因为图片选择的这个终点的关系，所以导致C方格上面或下面的格子的F值是一样的，也就是往上或下走路程都一样，这里暂且假设D方格是开启列表中第一位的元素。


4.然后用考察列表中第一位的元素(也就是D)与开启列表中的所有元素对比一遍，看看开启列表中有没有同样的格子(格子D)。如果有就计算一下当前格子C走到D的G值之和是否小于D本身的G值。例如C点本身的G值是10，往下走算直线，G值也是10,10+10=20，20>14；说明绕远路了。


5.如果发现绕远路了，就把C格子放入关闭列表，然后清空开启列表和关闭列表。因为条件不满足，我们并没有更新当前点的坐标，所以程序会再次循环，找出开启列表中F值最小的点，又因为C格子已经被加入关闭列表，所以它并不会被加入开启列表中，此时开启列表中F值最小的格子就是D了，选择D作为考察点，把D周围的除墙以外符合条件的点全部加入考察列表，再次选出考察列表第一位的格子与开启列表中对比，有重复就检测G值，没有重复就可以确定这个格子适合作为路径，就用考察点更新当前点，然后把考察点加入关闭列表，同时把当前点加入结果列表。

 

 

 

6.重复以上过程，直到开启列表中出现终点坐标，或者所有格子都加入了关闭列表导致开启列表为空，寻路结束。

 

 

 

 


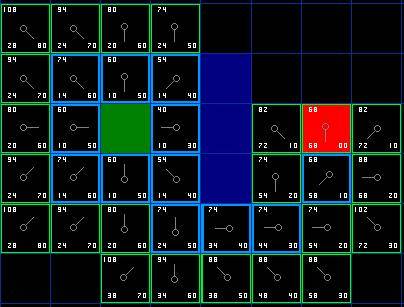
7.最后输出一下结果列表中的内容，就得到路径了。

 

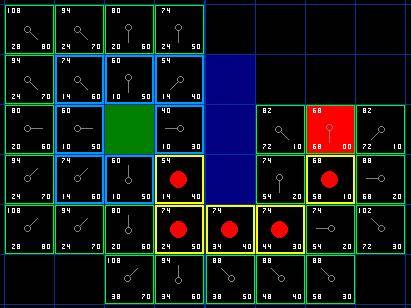
     到此就是A*算法的一个寻路判断逻辑，还有一个小问题前面没有提到，就是路过墙角的时候允许不允许算法走斜线，如果不允许，就需要在遍历当前点或者考察点的时候考虑这个因素，我的办法是在遍历周围点的时候加一个判断，如果上下左右4个方向有一个方向判断是墙，就关闭一个开关变量，使得后面不再考虑斜着的4个方向，这样一旦靠墙的时候就只会"直来直去"。

 

下面是算法伪代码：


网格结构体{

int x坐标
int y坐标

int f
int g
int h

}网格; --实例化一个网格结构体 

起点x
起点y

终点x
终点y


开启列表
list<网格>开启列表;

关闭列表
list<网格>关闭列表;

考察列表
list<网格>考察列表

结果列表  --存放着已经确定的最终路径，最后就要沿着这个路径走路
list<网格>结果列表


当前结构体

待考察结构体

初始化当前结构体

初始化待考察结构体


list<网格>::iterator 开启列表迭代器;  --创建4个迭代器
list<网格>::iterator 关闭列表迭代器;
list<网格>::iterator 考察列表迭代器;
list<网格>::iterator 结果列表迭代器;

当前结构体->y=y;

当前结构体->x=x;   --起点x,起点y 送入当前结构体

int 开关变量=1;
int prize=1  //另一个判断用变量

while(开关变量==1)
{

if(开启列表.empty()) --如果开启列表空了就说明没找到路，退出循环

{

   开关变量=0
   break;

}


if(开关变量==1)

{ 
    
   --把开启列表作为参数，遍历当前结构体周围8个格子的结果就会放入开启列表中等待检测 

   清空开启列表
 

   清空考察列表

 

 

   遍历8方向函数(开启列表,当前结构体->y,当前结构体->x)  

   for(开启列表迭代器=开启列表.begin();开启列表迭代器!=开启列表.end();开启列表迭代器++)

   {

       --看看开启列表里是否已经有终点坐标，如果有说明寻路成功

       if(开启列表迭代器->y==终点y && 开启列表迭代器->x==终点x)

       {

       开关变量=0
       prize=0
       break;

       --寻路成功就关闭开关变量就不会进行下面的动作，结束寻路

       }

   }


if(prize==1)
{

   开启列表.sort()  --按结构体内F值大小排序,由小到大

   开启列表迭代器=开启列表.begin();
   
   选出开启列表中的第一个元素放入考察结构体,并在开启列表中删除第一个元素    
   
    --因为按照排序规则第一个元素的F值最小

   遍历8方向函数(考察列表,开启列表迭代器->y,开启列表迭代器->x)  --遍历考察方格附近的8个格子,把结果放入考察列表

   考察列表.sort()  --给考察列表排个序

   考察列表迭代器=考察列表.begin()  --让迭代器指向考察列表第一个元素

   int 标志3=1;

   for(开启列表迭代器=开启列表.begin();开启列表迭代器!=考察列表.end();开启列表迭代器++)

   {

 

       --把考察列表的第一个元素与开启列表里的所有元素都匹配一遍，如果匹配上了，说明考察列表的第一个元素可能不是最短路径

     

 

       if(考察列表迭代器->x==开启列表迭代器->x && 考察列表迭代器->y==开启列表迭代器->y)

       {

               if(考察结构体->G + 考察列表迭代器->G > 开启列表迭代器->G)

              {
               --考察结构体里的G值+考察列表迭代器第一个元素里的G值如果大于当前开启列表迭代器指向的元素里的G值，说                 --明这条路线不划算。考虑到sort()方法排序的时候可能会把考察结构体里的格子上下的格子放在在更新后的开                --放列表的第一位或第二位，所以需要这样判断一下 

               考察结构体放入关闭列表
               清空考察列表
               标志3=0;
               break; --退出for循环
              }  

       }

   }

          if(标志3==1)
          {
              --如果上面的条件没满足说明现在开启列表第一位的格子是最佳路径

              考察结构体放入关闭列表
              考察结构体放入结果列表
              考察结构体放入当前结构体 --以进行下一次循环
          }

}

}

}


//*****************************

//遍历一个点周围格子的函数

void 遍历8方向函数(list<网格> &随便,需要遍历的y,需要遍历的x,int 终点y,int 终点x)
{

   --8方向判断
   int 判断标志,是否4方向;
   是否4方向=1; --默认8方向遍历
   if arr[y][x] ↑==1 then
   {

 

      判断标志=1;

      是否4方向=1;

      for(关闭列表迭代器=关闭列表.begin();关闭列表迭代器!=关闭列表.end();关闭列表迭代器++)
      {

           --如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表      

           if(关闭列表迭代器->y==y && 关闭列表迭代器->x==x)

           {

               判断标志=0;
               break;
               --条件满足了就跳出for循环
           }

      }

      if(判断标志==1)

      {

           网格结构体.春哥  --新建一个网格结构体

           --给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

           春哥.y=需要遍历的y-1
           春哥.y=需要遍历的x
           春哥.g=10
           春哥.h=abs(需要遍历的y-终点y) + abs(需要遍历的x-终点x)  --abs()是整数的取绝对值函数
           春哥.f=春哥.g+春哥.h

           随便.push_back(春哥); --从尾部插入元素

      }

   else

   {

   是否4方向=0;

   }

   }


   if arr[y][x] →==1 then
   {

    给这个格子的x,y赋值，然后分别计算f,g,h值,然后放入开启列表

   }

   if arr[y][x] ↓==1 then
   {

    给这个格子的x,y赋值，然后分别计算f,g,h值,然后放入开启列表

   }

   if arr[y][x] ←==1 then
   {

    给这个格子的x,y赋值，然后分别计算f,g,h值,然后放入开启列表

   }

 if(是否4方向==1)  --默认8方向寻路，如果==0就说明旁边有墙，就会4方向遍历

 {

   if arr[y][x] ↗==1 then
   {

    给这个格子的x,y赋值，然后分别计算f,g,h值,然后放入开启列表

   }


   if arr[y][x] ↘==1 then
   {

    给这个格子的x,y赋值，然后分别计算f,g,h值,然后放入开启列表

   }

   if arr[y][x] ↙==1 then
   {

    给这个格子的x,y赋值，然后分别计算f,g,h值,然后放入开启列表

   }


   if arr[y][x] ↖==1 then
   {

    给这个格子的x,y赋值，然后分别计算f,g,h值,然后放入开启列表

   }
 

 }


}


}

//***********************************
原点(1,1)

↑ (0,1)
Atlas[Current_Y-1][Current_X]

→(1,2)
Atlas[Current_Y][Current_X+1]

↓(2,1)
Atlas[Current_Y+1][Current_X]
←(1,0)
Atlas[Current_Y][Current_X-1]
↗(0,2)
Atlas[Current_Y-1][Current_X+1]

↘(2,2)
Atlas[Current_Y+1][Current_X+1]

↙(2,0)
Atlas[Current_Y+1][Current_X-1]

↖(0,0)
Atlas[Current_Y-1][Current_X-1]


.h文件

 

 

 

#pragma once
#include <string> 
#include <list>



//*****************************

typedef struct child
{
	int X,Y;  //坐标
	int F,G,H;  

}Someone;  //定义结构体的同时把结构体订一个别名




void StructureInput(Someone& classTemp,int y,int x,int f,int g,int h);  //结构体构造函数

//void ListClassInput(std::list <Someone>& classcopy, Someone &( hh.F));  //链表构造函数

bool CostComp(Someone first, Someone second); //排序函数

void Search_8(std::list <Someone>& classcopy,Someone &can,int End_Y,int End_X);//8方向搜索函数

void Way_Finding(int Starting_Y,int Starting_X,int End_Y,int End_X); //A*函数

 

.CPP文件

 

 

#include "stdafx.h"
#include "Feet.h"
#include <string> 
#include <list>

using namespace std;

//*********************************

int Atlas[11][7] ={  
	{0,0,0,0,0,0,0},
	{0,1,1,1,1,1,0},
	{0,1,1,1,0,1,0},
	{0,1,1,1,0,1,0},
	{0,1,1,1,0,1,0},
	{0,1,1,1,1,1,0},
	{0,1,1,1,0,1,0},
	{0,1,1,0,0,1,0},
	{0,1,0,0,0,1,0},
	{0,1,1,1,1,1,0},
	{0,0,0,0,0,0,0},

};



list <Someone>Openlist; //开启列表	 
list <Someone>Closelist; //关闭列表
list <Someone>Inspectlist; //考察列表
list <Someone>Resultlist;  //结果列表


list <Someone>::iterator OpenIter;  //开启列表迭代器
list <Someone>::iterator CloseIter; //关闭列表迭代器
list <Someone>::iterator InspectIter; //考察列表迭代器
list <Someone>::iterator ResultIter; //结果列表迭代器

Someone Current; //当前结构体
Someone Inspect; //考察结构体

//*********************************

void StructureInput(Someone& classTemp,int y,int x,int f,int g,int h)   //结构体构造函数  
{  
	classTemp.Y=y;
	classTemp.X=x;
	classTemp.F=f;
	classTemp.G=g;
	classTemp.H=h;

}  
/*
void ListClassInput(std::list <Someone>& classcopy,int hh) //链表输入函数
{ //之前测试时候的函数与本主题无关请无视	 
	//has-=1;
	Someone classtemp; //新建一个结构体
	for (int i=0;i!=hh;i++)
	{
		ClassInput(classtemp,arr_x[i],arr_y[i],6,6,6);  //给结构体里的成员赋值
		classcopy.push_front(classtemp); //赋值完后把结构体压入参数中的链表的第一个元素中
	}


}
*/



bool CostComp(Someone first, Someone second)  //排序函数
{

	return first.F<second.F;  //<为由小到大；改为>则由大到小

}



void Search_8(list <Someone>& classcopy,Someone &can,int End_Y,int End_X)  /*8方向搜索函数 Someone &can:当前结构体或者考察结构体*/
{
	int Current_Y,Current_X;  //当前要检测的点
	Current_Y=can.Y;
	Current_X=can.X;

	int Judge=1; //如果遇到拐角就选择4方向
	int others; //判断一个坐标是否在关闭列表中的标志变量

	if (Atlas[Current_Y-1][Current_X]==1)  //↑
	{

		others=1;

		for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
		{
			//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
			if (CloseIter->Y==Current_Y-1 && CloseIter->X==Current_X)
			{
				others=0;
				break; //条件满足就退出for循环

			}


		}

		if (others==1)
		{
			Someone chunge;  //实例化一个结构体
			//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中
			
			chunge.Y=Current_Y-1;
			chunge.X=Current_X;  //↑
			chunge.G=10;
			chunge.H=abs(chunge.Y-End_Y)+abs(chunge.X-End_X);
			chunge.F=chunge.G+chunge.H;

			classcopy.push_back(chunge); //把填充好的结构压入list

		}

		

	}

	else
	{


		Judge=0;
		//如果为0说明4方向上下左右有一个是墙，那就关闭8方向,选择4方向移动


	}





	if (Atlas[Current_Y][Current_X+1]==1)  //→
	{

		others=1;

		for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
		{
			//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
			if (CloseIter->Y==Current_Y && CloseIter->X==Current_X+1)
			{
				others=0;
				break; //条件满足就退出for循环

			}


		}

		if (others==1)
		{
			Someone chunge;  //实例化一个结构体
			//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

			chunge.Y=Current_Y;
			chunge.X=Current_X+1;  //→
			chunge.G=10;
			chunge.H=abs(chunge.Y-End_Y)+abs(chunge.X-End_X);
			chunge.F=chunge.G+chunge.H;

			classcopy.push_back(chunge); //把填充好的结构压入list

		}



	}

	else
	{


		Judge=0;
		//如果为0说明4方向上下左右有一个是墙，那就关闭8方向,选择4方向移动


	}





	if (Atlas[Current_Y+1][Current_X]==1)  //↓
	{

		others=1;

		for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
		{
			//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
			if (CloseIter->Y==Current_Y+1 && CloseIter->X==Current_X)
			{
				others=0;
				break; //条件满足就退出for循环

			}


		}

		if (others==1)
		{
			Someone chunge;  //实例化一个结构体
			//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

			chunge.Y=Current_Y+1;
			chunge.X=Current_X;  //↓
			chunge.G=10;
			chunge.H=abs(chunge.Y-End_Y)+abs(chunge.X-End_X);
			chunge.F=chunge.G+chunge.H;

			classcopy.push_back(chunge); //把填充好的结构压入list

		}



	}

	else
	{


		Judge=0;
		//如果为0说明4方向上下左右有一个是墙，那就关闭8方向,选择4方向移动


	}







	if (Atlas[Current_Y][Current_X-1]==1)  //←
	{

		others=1;

		for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
		{
			//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
			if (CloseIter->Y==Current_Y && CloseIter->X==Current_X-1)
			{
				others=0;
				break; //条件满足就退出for循环

			}


		}

		if (others==1)
		{
			Someone chunge;  //实例化一个结构体
			//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

			chunge.Y=Current_Y;
			chunge.X=Current_X-1;  //←
			chunge.G=10;
			chunge.H=abs(chunge.Y-End_Y)+abs(chunge.X-End_X);
			chunge.F=chunge.G+chunge.H;

			classcopy.push_back(chunge); //把填充好的结构压入list

		}



	}

	else
	{


		Judge=0;
		//如果为0说明4方向上下左右有一个是墙，那就关闭8方向,选择4方向移动


	}


//斜着的4个方向

if (Judge==1) 
{



	if (Atlas[Current_Y-1][Current_X+1]==1)  //↗
	{

		others=1;

		for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
		{
			//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
			if (CloseIter->Y==Current_Y-1 && CloseIter->X==Current_X+1)
			{
				others=0;
				break; //条件满足就退出for循环

			}


		}

		if (others==1)
		{
			Someone chunge;  //实例化一个结构体
			//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

			chunge.Y=Current_Y-1;
			chunge.X=Current_X+1;  //↗
			chunge.G=14;
			chunge.H=abs(chunge.Y-End_Y)+abs(chunge.X-End_X);
			chunge.F=chunge.G+chunge.H;

			classcopy.push_back(chunge); //把填充好的结构压入list

		}



	}





	if (Atlas[Current_Y+1][Current_X+1]==1)  //↘
	{

		others=1;

		for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
		{
			//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
			if (CloseIter->Y==Current_Y+1 && CloseIter->X==Current_X+1)
			{
				others=0;
				break; //条件满足就退出for循环

			}


		}

		if (others==1)
		{
			Someone chunge;  //实例化一个结构体
			//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

			chunge.Y=Current_Y+1;
			chunge.X=Current_X+1;  //↘
			chunge.G=14;
			chunge.H=abs(chunge.Y-End_Y)+abs(chunge.X-End_X);
			chunge.F=chunge.G+chunge.H;

			classcopy.push_back(chunge); //把填充好的结构压入list

		}



	}







	if (Atlas[Current_Y+1][Current_X-1]==1)  //↙
	{

		others=1;

		for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
		{
			//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
			if (CloseIter->Y==Current_Y+1 && CloseIter->X==Current_X-1)
			{
				others=0;
				break; //条件满足就退出for循环

			}


		}

		if (others==1)
		{
			Someone chunge;  //实例化一个结构体
			//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

			chunge.Y=Current_Y+1;
			chunge.X=Current_X-1;  //↙
			chunge.G=14;
			chunge.H=abs(chunge.Y-End_Y)+abs(chunge.X-End_X);
			chunge.F=chunge.G+chunge.H;

			classcopy.push_back(chunge); //把填充好的结构压入list

		}



	}





	if (Atlas[Current_Y-1][Current_X-1]==1)  //↖
	{

		others=1;

		for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
		{
			//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
			if (CloseIter->Y==Current_Y-1 && CloseIter->X==Current_X-1)
			{
				others=0;
				break; //条件满足就退出for循环

			}


		}

		if (others==1)
		{
			Someone chunge;  //实例化一个结构体
			//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

			chunge.Y=Current_Y-1;
			chunge.X=Current_X-1;  //↖
			chunge.G=14;
			chunge.H=abs(chunge.Y-End_Y)+abs(chunge.X-End_X);
			chunge.F=chunge.G+chunge.H;

			classcopy.push_back(chunge); //把填充好的结构压入list

		}



	}




}



}


void Way_Finding(int Starting_Y,int Starting_X,int End_Y,int End_X) //寻路函数参数：起点y,起点x,终点y,终点x
{
	int Switch_A=1; //开关变量
	int Switch_B=1; //开关变量
	StructureInput(Current,Starting_Y,Starting_X,0,0,0);//起点x,起点y 送入当前结构体

	Openlist.push_back(Current); //初始化开启列表
	Closelist.push_back(Current); //把起点放入关闭列表

     while(Switch_A==1)//开始寻路	
	{

	
	   if (Openlist.empty())    //如果开启列表空了就说明没找到路，退出循环
	  {

		    Switch_A=0;
			OutputDebugStringW(L"没找到路");
			break;

	   }
	   	  
		
		else if (Switch_A==1)
		{
			CString shall_Y,shall_X,Rather;  //测试用字符串变量


			Openlist.clear();//清空开启列表
			Inspectlist.clear(); //清空考察列表

			Search_8(Openlist,Current,End_Y,End_X); //首先遍历开始坐标周围8个格子 Current:当前结构体

			//检查一下开启列表里是否有终点坐标，如果有就结束寻路
			for (OpenIter=Openlist.begin();OpenIter!=Openlist.end();OpenIter++)
			{

				if (OpenIter->Y==End_Y && OpenIter->X==End_X)
				{


					Switch_A=0;
					Switch_B=0;				
					OutputDebugStringW(L"到终点了\n");
					break;
					//寻路成功就关闭开关变量就不会进行下面的动作，结束寻路

				}


			}


			if (Switch_B==1)
			{
			

			Openlist.sort(CostComp);  //按F大小排序

			OpenIter=Openlist.begin(); //让开启列表迭代器指向开启列表第一个元素

			//选出开启列表中的第一个元素放入考察结构体,并在开启列表中删除第一个元素
			StructureInput(Inspect,OpenIter->Y,OpenIter->X,OpenIter->F,OpenIter->G,OpenIter->H);//结构体赋值 Inspect:考察结构体

			Search_8(Inspectlist,Inspect,End_Y,End_X); //把考察点周围符合条件的点加入考察列表

			Inspectlist.sort(CostComp);  //考察列表排序

			InspectIter=Inspectlist.begin(); //让迭代器指向考察列表第一个元素


			int Happiness=1;  //控制下面流程的标志变量
			
			for (OpenIter=Openlist.begin();OpenIter!=Openlist.end();OpenIter++)
			{

				//把考察列表的第一个元素与开启列表里的所有元素都匹配一遍
				//如果匹配上了，说明考察列表的第一个元素可能不是最短路径

				if (InspectIter->Y==OpenIter->Y && InspectIter->X==OpenIter->X)
				{


					if (Inspect.G+InspectIter->G>OpenIter->G)
					{

						Happiness=0;
						Closelist.push_back(Inspect);//考察结构体放入关闭列表
						break; //退出for循环

					}


				}

				


			}

			if (Happiness==1)
			{
				//如果上面的条件没满足说明现在开启列表第一位的格子是最佳路径
				Closelist.push_back(Inspect);//考察结构体放入关闭列表
				Resultlist.push_back(Inspect);//考察结构体放入结果列表

				StructureInput(Current,Inspect.Y,Inspect.X,Inspect.F,Inspect.G,Inspect.H);//考察结构体放入当前结构体


			}


			}


		}

			

	}



}

 

void Search_4(list <Someone>& classcopy,Someone &can,int End_Y,int End_X)  /*4方向搜索函数 Someone &can:当前结构体或者考察结构体*/
{
	int Current_Y,Current_X;  //当前要检测的点
	Current_Y=can.Y;
	Current_X=can.X;
	double Selves;

	int others; //判断一个坐标是否在关闭列表中的标志变量

	if (Atlas[Current_Y-1][Current_X]==1)  //↑
	{

		others=1;

		for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
		{
			//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
			if (CloseIter->Y==Current_Y-1 && CloseIter->X==Current_X)
			{
				others=0;
				break; //条件满足就退出for循环

			}


		}

		if (others==1)
		{
			Someone chunge;  //实例化一个结构体
			//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中
			chunge.Y=Current_Y-1;
			chunge.X=Current_X;  //↑
			chunge.G=10;
			Selves=abs(chunge.Y-End_Y)*abs(chunge.Y-End_Y)+abs(chunge.X-End_X)*abs(chunge.X-End_X);
			chunge.H=int(sqrt(Selves)+0.5);//四舍五入后截尾转为int型
			chunge.F=chunge.G+chunge.H;

			classcopy.push_back(chunge); //把填充好的结构压入list

		}



	}





	if (Atlas[Current_Y][Current_X+1]==1)  //→
	{

		others=1;

		for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
		{
			//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
			if (CloseIter->Y==Current_Y && CloseIter->X==Current_X+1)
			{
				others=0;
				break; //条件满足就退出for循环

			}


		}

		if (others==1)
		{
			Someone chunge;  //实例化一个结构体
			//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

			chunge.Y=Current_Y;
			chunge.X=Current_X+1;  //→
			chunge.G=10;
			Selves=abs(chunge.Y-End_Y)*abs(chunge.Y-End_Y)+abs(chunge.X-End_X)*abs(chunge.X-End_X);
			chunge.H=int(sqrt(Selves)+0.5);//四舍五入后截尾转为int型
			chunge.F=chunge.G+chunge.H;

			classcopy.push_back(chunge); //把填充好的结构压入list

		}



	}





	if (Atlas[Current_Y+1][Current_X]==1)  //↓
	{

		others=1;

		for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
		{
			//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
			if (CloseIter->Y==Current_Y+1 && CloseIter->X==Current_X)
			{
				others=0;
				break; //条件满足就退出for循环

			}


		}

		if (others==1)
		{
			Someone chunge;  //实例化一个结构体
			//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

			chunge.Y=Current_Y+1;
			chunge.X=Current_X;  //↓
			chunge.G=10;
			Selves=abs(chunge.Y-End_Y)*abs(chunge.Y-End_Y)+abs(chunge.X-End_X)*abs(chunge.X-End_X);
			chunge.H=int(sqrt(Selves)+0.5);//四舍五入后截尾转为int型
			chunge.F=chunge.G+chunge.H;

			classcopy.push_back(chunge); //把填充好的结构压入list

		}



	}






	if (Atlas[Current_Y][Current_X-1]==1)  //←
	{

		others=1;

		for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
		{
			//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
			if (CloseIter->Y==Current_Y && CloseIter->X==Current_X-1)
			{
				others=0;
				break; //条件满足就退出for循环

			}


		}

		if (others==1)
		{
			Someone chunge;  //实例化一个结构体
			//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

			chunge.Y=Current_Y;
			chunge.X=Current_X-1;  //←
			chunge.G=10;
			Selves=abs(chunge.Y-End_Y)*abs(chunge.Y-End_Y)+abs(chunge.X-End_X)*abs(chunge.X-End_X);
			chunge.H=int(sqrt(Selves)+0.5);//四舍五入后截尾转为int型
			chunge.F=chunge.G+chunge.H;

			classcopy.push_back(chunge); //把填充好的结构压入list

		}



	}



}

 

 

 

欧几里得算法计算H值：

使用sqrt()开方函数需要引入头文件

#include <math.h>

void Search_8(list <Someone>& classcopy,Someone &can,int End_Y,int End_X)  //8方向搜索函数 Someone &can:当前结构体或者考察结构体
{
	int Current_Y,Current_X;  //当前要检测的点
	Current_Y=can.Y;
	Current_X=can.X;
	double Selves;

	int Judge=1; //如果遇到拐角就选择4方向
	int others; //判断一个坐标是否在关闭列表中的标志变量

	if (Atlas[Current_Y-1][Current_X]==1)  //↑
	{

		others=1;

		for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
		{
			//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
			if (CloseIter->Y==Current_Y-1 && CloseIter->X==Current_X)
			{
				others=0;
				break; //条件满足就退出for循环

			}


		}

		if (others==1)
		{
			Someone chunge;  //实例化一个结构体
			//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中
			chunge.Y=Current_Y-1;
			chunge.X=Current_X;  //↑
			chunge.G=10;
			Selves=abs(chunge.Y-End_Y)*abs(chunge.Y-End_Y)+abs(chunge.X-End_X)*abs(chunge.X-End_X);
			chunge.H=int(sqrt(Selves)+0.5);//四舍五入后截尾转为int型
			chunge.F=chunge.G+chunge.H;

			classcopy.push_back(chunge); //把填充好的结构压入list

		}



	}

	else
	{


		Judge=0;
		//如果为0说明4方向上下左右有一个是墙，那就关闭8方向,选择4方向移动


	}





	if (Atlas[Current_Y][Current_X+1]==1)  //→
	{

		others=1;

		for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
		{
			//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
			if (CloseIter->Y==Current_Y && CloseIter->X==Current_X+1)
			{
				others=0;
				break; //条件满足就退出for循环

			}


		}

		if (others==1)
		{
			Someone chunge;  //实例化一个结构体
			//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

			chunge.Y=Current_Y;
			chunge.X=Current_X+1;  //→
			chunge.G=10;
			Selves=abs(chunge.Y-End_Y)*abs(chunge.Y-End_Y)+abs(chunge.X-End_X)*abs(chunge.X-End_X);
			chunge.H=int(sqrt(Selves)+0.5);//四舍五入后截尾转为int型
			chunge.F=chunge.G+chunge.H;

			classcopy.push_back(chunge); //把填充好的结构压入list

		}



	}

	else
	{


		Judge=0;
		//如果为0说明4方向上下左右有一个是墙，那就关闭8方向,选择4方向移动


	}





	if (Atlas[Current_Y+1][Current_X]==1)  //↓
	{

		others=1;

		for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
		{
			//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
			if (CloseIter->Y==Current_Y+1 && CloseIter->X==Current_X)
			{
				others=0;
				break; //条件满足就退出for循环

			}


		}

		if (others==1)
		{
			Someone chunge;  //实例化一个结构体
			//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

			chunge.Y=Current_Y+1;
			chunge.X=Current_X;  //↓
			chunge.G=10;
			Selves=abs(chunge.Y-End_Y)*abs(chunge.Y-End_Y)+abs(chunge.X-End_X)*abs(chunge.X-End_X);
			chunge.H=int(sqrt(Selves)+0.5);//四舍五入后截尾转为int型
			chunge.F=chunge.G+chunge.H;

			classcopy.push_back(chunge); //把填充好的结构压入list

		}



	}

	else
	{


		Judge=0;
		//如果为0说明4方向上下左右有一个是墙，那就关闭8方向,选择4方向移动


	}







	if (Atlas[Current_Y][Current_X-1]==1)  //←
	{

		others=1;

		for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
		{
			//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
			if (CloseIter->Y==Current_Y && CloseIter->X==Current_X-1)
			{
				others=0;
				break; //条件满足就退出for循环

			}


		}

		if (others==1)
		{
			Someone chunge;  //实例化一个结构体
			//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

			chunge.Y=Current_Y;
			chunge.X=Current_X-1;  //←
			chunge.G=10;
			Selves=abs(chunge.Y-End_Y)*abs(chunge.Y-End_Y)+abs(chunge.X-End_X)*abs(chunge.X-End_X);
			chunge.H=int(sqrt(Selves)+0.5);//四舍五入后截尾转为int型
			chunge.F=chunge.G+chunge.H;

			classcopy.push_back(chunge); //把填充好的结构压入list

		}



	}

	else
	{


		Judge=0;
		//如果为0说明4方向上下左右有一个是墙，那就关闭8方向,选择4方向移动


	}


	//斜着的4个方向

	if (Judge==1) 
	{



		if (Atlas[Current_Y-1][Current_X+1]==1)  //↗
		{

			others=1;

			for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
			{
				//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
				if (CloseIter->Y==Current_Y-1 && CloseIter->X==Current_X+1)
				{
					others=0;
					break; //条件满足就退出for循环

				}


			}

			if (others==1)
			{
				Someone chunge;  //实例化一个结构体
				//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

				chunge.Y=Current_Y-1;
				chunge.X=Current_X+1;  //↗
				chunge.G=14;
				Selves=abs(chunge.Y-End_Y)*abs(chunge.Y-End_Y)+abs(chunge.X-End_X)*abs(chunge.X-End_X);
				chunge.H=int(sqrt(Selves)+0.5);//四舍五入后截尾转为int型
				chunge.F=chunge.G+chunge.H;

				classcopy.push_back(chunge); //把填充好的结构压入list

			}



		}





		if (Atlas[Current_Y+1][Current_X+1]==1)  //↘
		{

			others=1;

			for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
			{
				//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
				if (CloseIter->Y==Current_Y+1 && CloseIter->X==Current_X+1)
				{
					others=0;
					break; //条件满足就退出for循环

				}


			}

			if (others==1)
			{
				Someone chunge;  //实例化一个结构体
				//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

				chunge.Y=Current_Y+1;
				chunge.X=Current_X+1;  //↘
				chunge.G=14;
				Selves=abs(chunge.Y-End_Y)*abs(chunge.Y-End_Y)+abs(chunge.X-End_X)*abs(chunge.X-End_X);
				chunge.H=int(sqrt(Selves)+0.5);//四舍五入后截尾转为int型
				chunge.F=chunge.G+chunge.H;

				classcopy.push_back(chunge); //把填充好的结构压入list

			}



		}







		if (Atlas[Current_Y+1][Current_X-1]==1)  //↙
		{

			others=1;

			for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
			{
				//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
				if (CloseIter->Y==Current_Y+1 && CloseIter->X==Current_X-1)
				{
					others=0;
					break; //条件满足就退出for循环

				}


			}

			if (others==1)
			{
				Someone chunge;  //实例化一个结构体
				//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

				chunge.Y=Current_Y+1;
				chunge.X=Current_X-1;  //↙
				chunge.G=14;
				Selves=abs(chunge.Y-End_Y)*abs(chunge.Y-End_Y)+abs(chunge.X-End_X)*abs(chunge.X-End_X);
				chunge.H=int(sqrt(Selves)+0.5);//四舍五入后截尾转为int型
				chunge.F=chunge.G+chunge.H;

				classcopy.push_back(chunge); //把填充好的结构压入list

			}



		}





		if (Atlas[Current_Y-1][Current_X-1]==1)  //↖
		{

			others=1;

			for (CloseIter=Closelist.begin();CloseIter!=Closelist.end();CloseIter++)
			{
				//如果在关闭列表里匹配到相同的格子，就什么都不做，不再把格子放入开启列表
				if (CloseIter->Y==Current_Y-1 && CloseIter->X==Current_X-1)
				{
					others=0;
					break; //条件满足就退出for循环

				}


			}

			if (others==1)
			{
				Someone chunge;  //实例化一个结构体
				//给这个网格结构体的x,y赋值，然后分别计算f,g,h值,然后放入开启列表或考察列表中

				chunge.Y=Current_Y-1;
				chunge.X=Current_X-1;  //↖
				chunge.G=14;
				Selves=abs(chunge.Y-End_Y)*abs(chunge.Y-End_Y)+abs(chunge.X-End_X)*abs(chunge.X-End_X);
				chunge.H=int(sqrt(Selves)+0.5); //四舍五入后截尾转为int型
				chunge.F=chunge.G+chunge.H;

				classcopy.push_back(chunge); //把填充好的结构压入list

			}



		}




	}



}

 

 

 

 

编译后点击确定运行：

 


其中数字 1 是可以行动的路，0 是墙， 7 是起点，5 是终点，6 是路径。

 

 

 

 

 

 

欧几里得算法与曼哈顿算法的对比：

 

曼哈顿算法：

 

欧几里得算法：

 

事实证明不能懒啊，之前写程序的时候懒得去查开方和四舍五入的函数，看来还是欧几里得算法计算H值比较接近事实。

 

参考文章:https://blog.youkuaiyun.com/u012234115/article/details/47152137

示例程序：https://download.youkuaiyun.com/download/l198738655/11834969

A*算法求解八数码--演示程序（MFC）
Onwaier的博客
05-11 6850
首先看看程序的运行效果 一、程序功能： 1、单步或者连续演示用A*解决八数码或者十五数码难题的步骤，可暂停。 2、随机生成初始状态。 3、调节演示速度（加快与减慢） 4、open表与close表对应存储的为未扩展结点和已扩展的结点。 5、演示完毕，显示最优路径。 二、预备知识 1、八数码与A*算法 A*算法：A*算法是一种有序搜索算法，其特点在于对估价函数的定义上。对于一般的...
A*算法附c++代码
qq_45620703的博客
07-01 2897
一.什么是a* 一种十分常用的寻路算法，它能够依据某个或某些优化准则，在空间中找到一个从起始点到目标点能避开障碍物的最优路径。 二.算法 以下图为例，敌人要绕过中间的障碍物，寻找到敌人。（以一个方块作为一个节点） 大概思路 1.首先将敌人所在的节点（起始点）加入到开列表中（接下来可能会用到的节点） 2.从开列表中取出花费值最小的节点（等会会讲到如何求花费值）（当前开列表中就一个节点）作为当前点 3.将当前点加入到闭列表中（已经用过的点，也是最后所需的点） 4.遍历当前点周围的点，搜索能通过的点(不是障碍物
A星寻路不贴墙多线程插件
最新发布
gitblog_06743的博客
04-14 228
A星寻路不贴墙多线程插件 【下载地址】A星寻路不贴墙多线程插件 这款A星寻路插件集高效、灵活与便捷于一身，专为路径规划需求设计。采用经典的A星算法，确保寻路过程精准快速，路径优化效果显著。独特的不贴墙特性，让角色在移动时更加自然，避免紧贴墙壁的尴尬。多线程支持则大幅提升寻路效率，充分利用系统资源，轻松应对复杂场景。插件内...
A*算法的实现——MFC编写
05-30
A*算法程序设计的实现——MFC编写 如题 包含了怎么用MFC创建和核心代码，工程代码会在之后打包上传，查看我其他资源
A*算法详解
z_mz11的博客
03-27 1588
A*（A-Star）算法是一种启发式搜索算法，广泛应用于路径规划和图遍历问题。A*算法的核心思想是：在搜索过程中，通过评估函数f(n)来选择最有希望的节点进行扩展，从而找到从起点到目标点的最短路径。
A星寻路算法 MFC写的动态演示程序
08-11
A星寻路算法 MFC写的动态演示程序 在上一版的基础上解决画面闪烁、单线程问题，加入暂停功能。加入斜向移动的功能。
MFC 基于单文档的A*算法小程序
08-04
很有意思的一个寻径小程序，支持自绘起点和终点，以及中间的各种障碍。
A星寻路算法&B星寻路算法 c++实现 MFC
11-26
总之，这个项目提供了C++实现的A星和B星寻路算法，结合MFC创建了一个可视化环境，用户可以观察和比较不同算法的寻路效果。通过调试和优化，这些算法可以应用于各种需要寻找最短路径的问题中，比如游戏中的角色移动、...
深入理解A*寻路算法及其C++实现
标题“A* A Star寻路算法”指明了我们要讨论的内容是A*算法，这是一种广泛应用于计算机科学中的路径寻找和图遍历算法。A*算法被设计为在图形平面上，从初始节点走到目标节点时，能够找到一条成本最低的路径。 描述...
广度优先算法、最佳优先算法、A*算法寻路程序
06-21
本项目重点介绍了三种常见的寻路算法：广度优先算法（Breadth-First Search, BFS）、最佳优先算法（Best-First Search）以及A*（A-star）算法，并通过C++语言在Visual Studio 2015环境下实现，使用MFC库进行可视化...
A星算法MFC实现和操作步骤
05-30
A星算法MFC实现和操作步骤.rar A算法程序设计 本程序用于实现例3.3中的10 x 10个方格中从指定起点到指定终点的最短路径，其中 可以在任意方格中放置障碍。对于10 x 10个方格使用二维数组m_a[10] [10]表示，每个 方格用数组元素表示。 A*算法的实现——MFC编写
mfc vc c++ navmesh自动寻路（改）
09-18
平面构建网格实现自动寻路，navmesh （修复不能直接编译问题）
A*算法源码（这是简单版本，更优版本已经上传）
08-11
A星寻路算法（A*算法）源码实现，用MFC程序模拟动态寻路过程。只实现了最简单的A*算法，MFC消息处理的也不好，仅作参考。
最短路径：计算任意两城市的最短路径（MFC界面）
06-28
能够计算任意两个城市的最短距离 1、具备城市输入功能，输入数据包含两个相邻城市的名称和间距； 2、查询两个城市的最短路径，输入为两个城市的名称，输出为两个城市间的最短路径。
非常完整的A*算法具体实例代码
11-17
这是A*算法的最短路径搜索代码，代码完整，可以直接打开运行，也可以直接拷贝到需要用的项目中。 注释非常详细，小白一看就能懂，附带伪代码 一步步看 大家多多学习又不明白可以联系
C++实现的寻路算法展示：广度优先、最佳优先与A*算法
在详细阐述这三个寻路算法之前，我们需要先了解寻路算法在计算机科学中的重要性。寻路问题广泛存在于游戏开发、人工智能、机器人导航等领域。它是指在一个有向或无向的图中，寻找到达目标点的最优或有效的路径。在该...
一个关于寻路算法的小程序
free4wuyou的专栏
11-15 696
http://qiao.github.io/PathFinding.js/visual/
unity3d寻路算法
tutututu12345678的博客
02-04 412
无论选择哪种方法，都取决于项目的需求和复杂性。对于简单的场景，导航网格可能是更容易实现和管理的选择。对于需要更高级定制和控制的情况，A*算法可能是更合适的选择。导航网格是一种用于寻路的高效技术。在场景中创建一个导航网格，代表可行走的区域，然后使用Unity3D的内置导航系统来寻找路径。Unity3D支持多种寻路算法，其中最常用的是导航网格（NavMesh）和A*算法。A*（A星）是一种基于图的搜索算法，用于在图形结构中找到最短路径。它通过评估每个可能的路径来找到最优解。
评论 5
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值