一、决策树概述
1.决策树(decision tree):是一种基本的分类与回归方法,此处主要讨论分类的决策树。
在分类问题中,表示基于特征对实例进行分类的过程,可以认为是if-then的集合,也可以认为是定义在特征空间与类空间上的条件概率分布。
决策树通常有三个步骤:特征选择、决策树的生成、决策树的修剪。
用决策树分类:从根节点开始,对实例的某一特征进行测试,根据测试结果将实例分配到其子节点,此时每个子节点对应着该特征的一个取值,如此递归的对实例进行测试并分配,直到到达叶节点,最后将实例分到叶节点的类中。
如下图(决策树示意图),圆点——内部节点,方框——叶节点
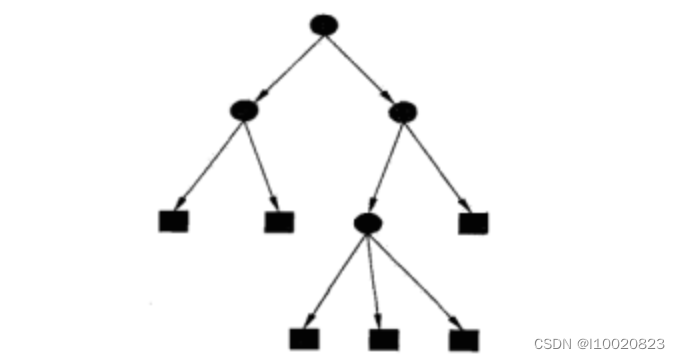
二、决策树的构建
1.ID3算法
ID3相当于用极大似然法进行概率模型的选择,核心是在决策树各个结点上对应信息增益准则选择特征,递归地构建决策树。
具体方法是:
1)从根结点(root node)开始,对结点计算所有可能的特征的信息增益,选择信息增益最大的特征作为结点的特征。
2)由该特征的不同取值建立子节点,再对子结点递归地调用以上方法,构建决策树;直到所有特征的信息增益均很小或没有特征可以选择为止;
3)最后得到一个决策树。
算法(ID3算法)
输入:训练数据集D,特征集A,阈值ε; 输出:决策树T.
(1)若D中所有实例属于同一类C(k),则T为单结点树,并将类C(k),作为该结点的类标记,返回T;
(2)若A=∅,则T为单结点树,并将D中实例数最大的类C(k)作为该结点的类标记,返回T;
(3)否则,按算法5.1计算A中各特征对D的信息增益,选择信息增益最大的特征A(k);
(4)如果A(k).的信息增益小于阈值ε,则置T为单结点树,并将D中实例数最大的类C,作为该结点的类标记,返回T;
(5)否则,对A(k)。的每一可能值a(i),依A(k)。=a(i),将D分割为若干非空子集D(i),将 D(i),中实例数最大的类作为标记,构建子结点,由结点及其子结点构成树T,返回T;
(6)对第i个子结点,以D(i),为训练集,以A-{A(k)}为特征集,递归地调用步(1)~步(5),得到子树T(i),返回T(i).
2.C4.5的生成算法
与ID3算法相似,但是做了改进,将信息增益比作为选择特征的标准。
递归构建决策树:
从数据集构造决策树算法所需的子功能模块工作原理如下:得到原始数据集,然后基于最好的属性值划分数据集,由于特征值可能多于两个,因此可能存在大于两个分支的数据集划分,第一次划分之后,数据将被向下传递到树分支的下一个节点,在此节点在此划分数据,因此可以使用递归的原则处理数据集。
递归结束的条件是:
程序完全遍历所有划分数据集的属性,或者每个分支下的所有实例都具有相同的分类,如果所有实例具有相同的分类,则得到一个叶子节点或者终止块,任何到达叶子节点的数据必然属于叶子节点的分类。
算法(4.5算法)
输入:训练数据集D,特征集A,阈值ε
输出:决策树T
(1)如果D中所有实例属于同一类Ck,则置T为单结点树,并将Ck作为该结点的类,返回T
(2) 如果A=Ø,则置T为单结点树,并将D中实例数最大的类Ck作为该结点的类,返回T
(3)否则,按式(1)计算A中各特征对D的信息增益比,选择信息增益比最大的特征Ag
(4)如果Ag的信息增益比小于阈值ε,则置T为单结点树,并将D中实例数最大的类Ck作为该结点的类,返回T
(5)否则,对Ag的每一可能值ai,依Ag=ai将D分割为若干非空子集Di,将Di中实例数最大的类作为标记,构建子结点,由结点及其子结点构成树T,返回T
(6)对结点i,以Di为训练集,以A-{Ag}为特征集,递归地调用①~⑤,得到子树Ti,返回Ti\
3.CART算法
CART决策树全称为Classification and Regression Tree,可以应用于分类和回归
CART使用了 CCP代价复杂度剪枝算法,对C4.5的剪枝方法进行了优化。
针对C4.5的多叉树的问题,CART改成了二叉树。
CART可以分为CART分类树和CART回归树。
采用基尼系数来划分属性
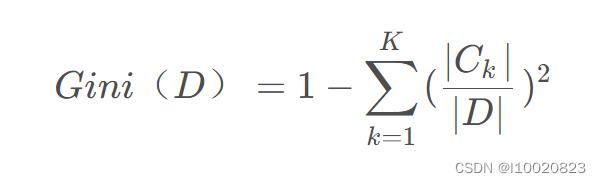
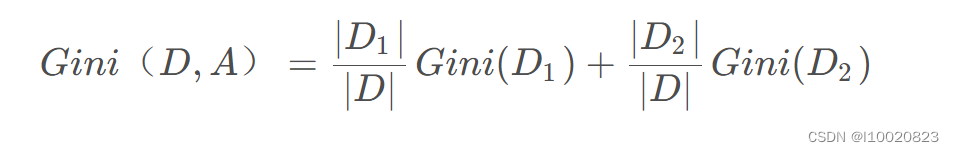
三、决策树模型的代码实现
1. 分类决策树模型(DecisionTreeClassifier)
from sklearn.tree import DecisionTreeClassifier
# X是特征变量,共有5个训练数据,每个数据有2个特征,如数据[1,2],它的第1个特征的数值为1,第2个特征的数值为2。
X = [[1,2],[3,4],[5,6],[7,8],[9,10]]
# 目标变量,共有2个类别——0和1。
y = [1,0,0,1,1]
# 第4行代码引入模型并设置随机状态参数random_state为0
# 这里的0没有特殊含义,可换成其他数字。它是一个种子参数,可使每次运行结果一致。
model = DecisionTreeClassifier(random_state=0)
model.fit(X,y)
model.predict([[5,5]])
# 输出结果
# array([0])
可以看到,数据[5,5]被预测为类别0。
为便于理解,将决策树可视化(方法见后边),效果如下图所示:
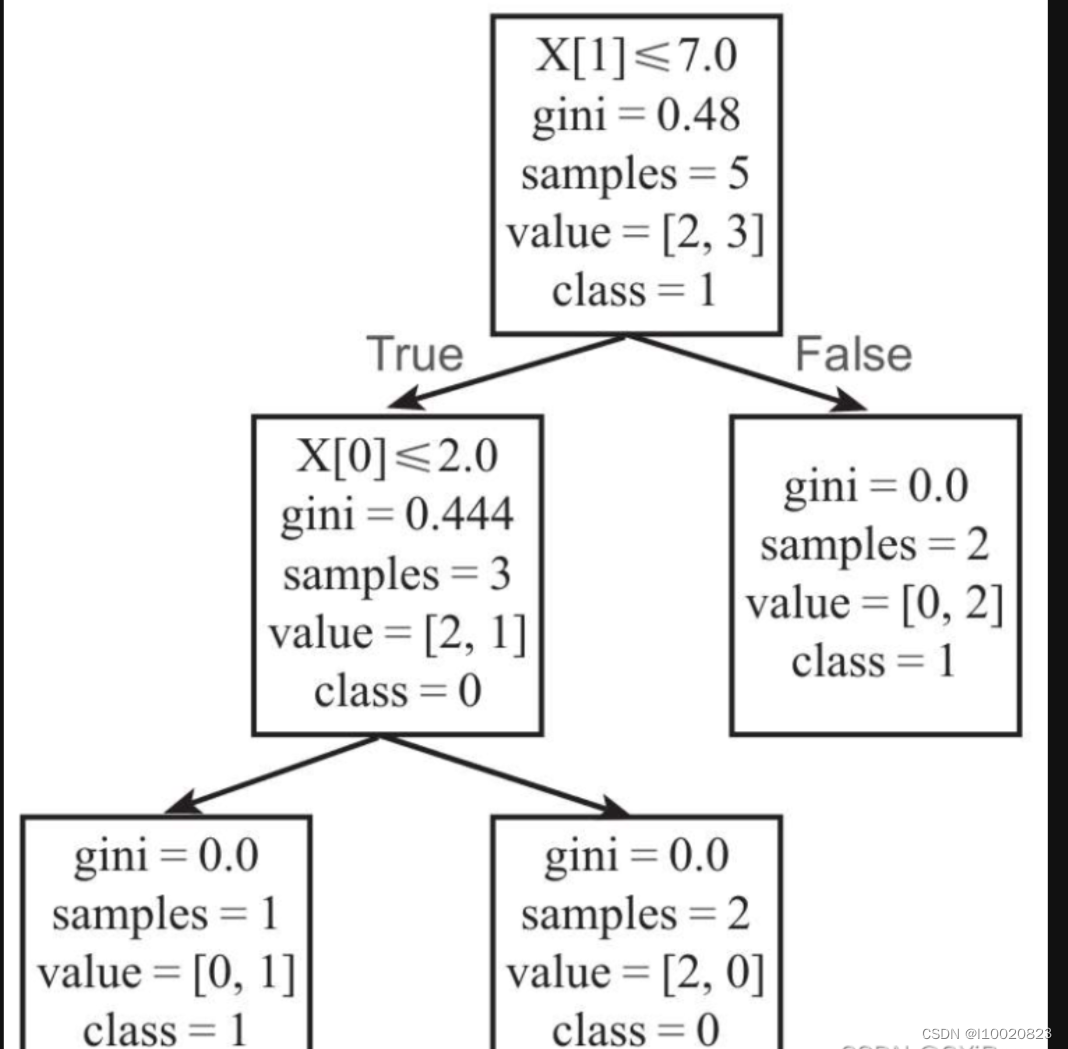
·X[0]表示数据的第1个特征;
·X[1]表示数据的第2个特征;
·gini表示该节点的基尼系数,以根节点为例,它的基尼系数为1-(0.42+0.62)=0.48;
·samples表示该节点的样本数;
·value表示各分类的样本数,例如,根节点中的[2,3]表示分类为0的样本数为2,分类为1的样本数为3;
·class表示该区块被划分为的类别,是由value中样本数较多的类别决定的.
2.回归决策树模型(DecisionTreeRegressor)
决策树除了能进行分类分析,还能进行回归分析,即预测连续变量,此时的决策树称为回归决策树。
from sklearn.tree import DecisionTreeRegressor
X = [[1,2],[3,4],[5,6],[7,8],[9,10]]
y = [1,2,3,4,5]
model = DecisionTreeRegressor(max_depth=2,random_state=0)
model.fit(X,y)
model.predict([[9,9]])
# 输出
array([4.5])
可以看到,数据[9,9]的预测拟合值为4.5。
回归决策树模型的概念和分类决策树模型基本一致,最大的不同就是其划分标准不是基尼系数或信息熵,而是均方误差MSE.
将决策树可视化,如下图所示。
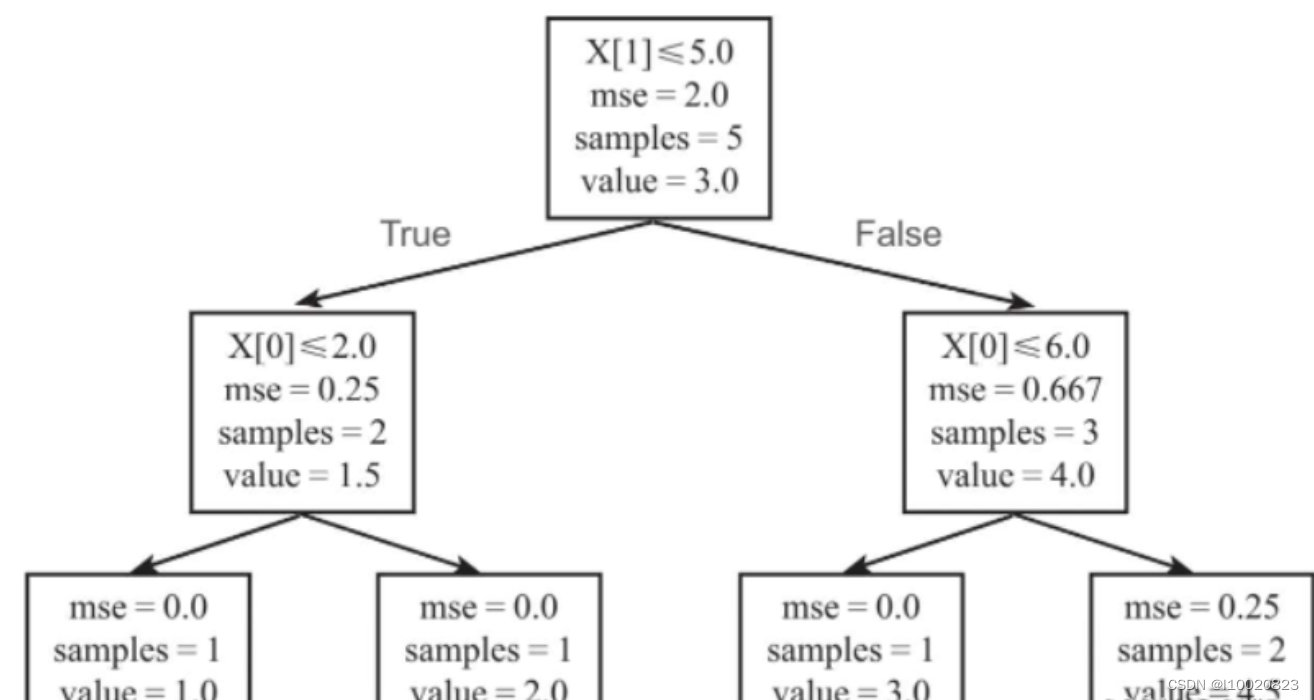
图中的X[0]表示数据的第1个特征,X[1]表示数据的第2个特征;mse表示该节点的均方误差;samples表示该节点的样本数;value表示该节点的拟合值,在回归决策树中,节点的拟合值是节点中所有数据的均值,最终的叶子节点的拟合值就是最终的回归模型预测值。
举例来说,根节点中一共有5个数据,其拟合值=(1+2+3+4+5)/5=3,其均方误差MSE的计算过程如下所示,结果为2.
四、总结
1. ID3、C4.5、CAR三种决策树算法比较
ID3算法:
ID3算法核心就是“最大信息熵增益” 原则选择划分当前数据集的最好特征。
而且对于连续型特征,比如长度,密度都是连续值,无法在ID3运用,因为一开始我用的鸢尾花实例数据,ID3不能判断连续型量。
前面也说到了,利用信息熵划分属性,会对倾向于可取值数目较多的属性。
没有考虑过拟合的问题。
C4.5算法:
- C4.5算法流程与ID3算法相类似,只不过将信息增益改为信息增益率,以解决偏向取值较多的属性的问题。
- 可以处理属性变量为连续型的,将连续的特征离散化。
CAR算法:
- CART算法使用基尼系数来代替信息增益比,基尼系数代表了模型的不纯度,基尼系数越小,则不纯度越低,特征越好。这和信息增益及信息增益率是相反的。
- 对于CART算法的连续值的处理问题,其思想和C4.5算法是相同的,都是将连续的特征离散化。
2.决策树的特点
优点:
容易理解,可解释性较好
可以用于小数据集
时间复杂度较小
可以处理多输入问题,可以处理不相关特征数据
对缺失值不敏感
缺点:
在处理特征关联性比较强的数据时,表现得不太好
当样本中各类别不均匀时,信息增益会偏向于那些具有更多数值的特征
对连续性的字段比较难预测
容易出现过拟合
当类别太多时,错误可能会增加得比较快























 1544
1544

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








