数据结构与算法——并查集 动画演示

于 2020-02-09 14:12:24 发布
阅读量788 收藏 1
点赞数 1
分类专栏： 数据结构与算法视频
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/l0919160205/article/details/104185713
版权
本文深入讲解并查集的基础概念、实现方式及优化策略，包括QuickFind、QuickUnion、基于size和rank的优化以及路径压缩技术，旨在提升算法效率。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

文章目录

一、并查集基础

    并查集是用来解决连接问题，如网络中结点的连接状态，如下图两个点是否相连等等这类连接问题，还可以实现数学中的集合。
在这里插入图片描述
    连接问题只需要回答是否连接，路径问题则是要找到路径。

    对于一组数据，并查集主要支持两个动作：
        union( p , q )//p和q连接起来
        find( p )//查p在哪个组中
    用来回答一个问题：
        isConnected( p , q )//p和q是否连接

并查集的实现

方式一：Qucik Find

    用数组来实现并查集，数组ID表示元素，数组的值表示集合，如下图：
在这里插入图片描述
Quick Find 时间复杂度 O(1)
Quick Find 下的 Union 时间复杂度 O(n)

代码如下：

// 我们的第一版Union-Find
namespace UF1 {

    class UnionFind {

    private:
        int *id;    // 我们的第一版Union-Find本质就是一个数组
        int count;  // 数据个数

    public:
        // 构造函数
        UnionFind(int n) {
            count = n;
            id = new int[n];
            // 初始化, 每一个id[i]指向自己, 没有合并的元素
            for (int i = 0; i < n; i++)
                id[i] = i;
        }

        // 析构函数
        ~UnionFind() {
            delete[] id;
        }

        // 查找过程, 查找元素p所对应的集合编号
        int find(int p) {
            assert(p >= 0 && p < count);
            return id[p];
        }

        // 查看元素p和元素q是否所属一个集合
        // O(1)复杂度
        bool isConnected(int p, int q) {
            return find(p) == find(q);
        }

        // 合并元素p和元素q所属的集合
        // O(n) 复杂度
        void unionElements(int p, int q) {

            int pID = find(p);
            int qID = find(q);

            if (pID == qID)
                return;

            // 合并过程需要遍历一遍所有元素, 将两个元素的所属集合编号合并
            for (int i = 0; i < count; i++)
                if (id[i] == pID)
                    id[i] = qID;
        }
    };
}

方式二：Quick Union

    将每一个元素看做一个结点，每一个结点指向根节点。每个元素只需要存父节点parent即可。如果两个元素需要合并，只需要将其中一个元素的根节点连接另一个元素的根节点。
    并操作只需要连接两个元素所在的根即可；
    查操作只需要查看两个元素是否是相同的根节点。
并操作union动画演示：
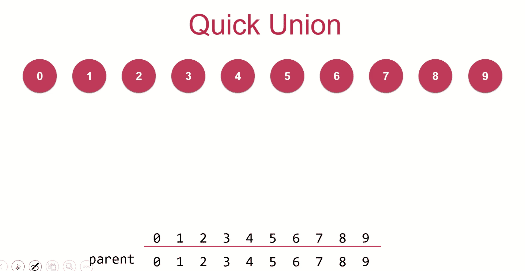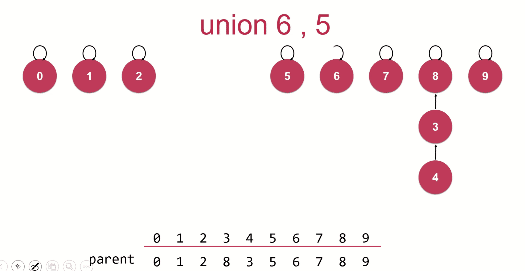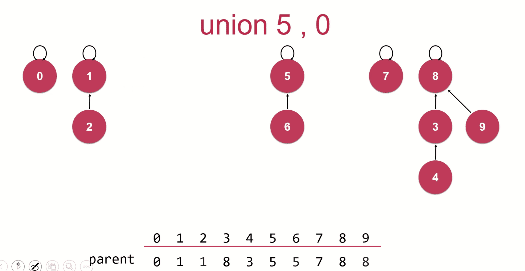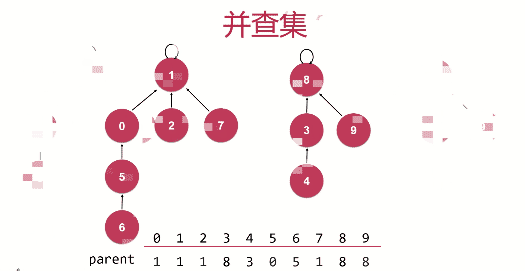
在这里插入图片描述
代码如下：

// 我们的第二版Union-Find
namespace UF2{

    class UnionFind{

    private:
        // 我们的第二版Union-Find, 使用一个数组构建一棵指向父节点的树
        // parent[i]表示第i个元素所指向的父节点
        int* parent;
        int count;  // 数据个数

    public:
        // 构造函数
        UnionFind(int count){
            parent = new int[count];
            this->count = count;
            // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
            for( int i = 0 ; i < count ; i ++ )
                parent[i] = i;
        }

        // 析构函数
        ~UnionFind(){
            delete[] parent;
        }

        // 查找过程, 查找元素p所对应的集合编号
        // O(h)复杂度, h为树的高度
        int find(int p){
            assert( p >= 0 && p < count );
            // 不断去查询自己的父亲节点, 直到到达根节点
            // 根节点的特点: parent[p] == p
            while( p != parent[p] )
                p = parent[p];
            return p;
        }

        // 查看元素p和元素q是否所属一个集合
        // O(h)复杂度, h为树的高度
        bool isConnected( int p , int q ){
            return find(p) == find(q);
        }

        // 合并元素p和元素q所属的集合
        // O(h)复杂度, h为树的高度
        void unionElements(int p, int q){

            int pRoot = find(p);
            int qRoot = find(q);

            if( pRoot == qRoot )
                return;

            parent[pRoot] = qRoot;
        }
    };
}

二、并查集的优化

优化一：基于size的优化

   如下图所示，合并元素9和元素4：
合并前：
在这里插入图片描述
合并后：
在这里插入图片描述
如果合并元素4和元素9：
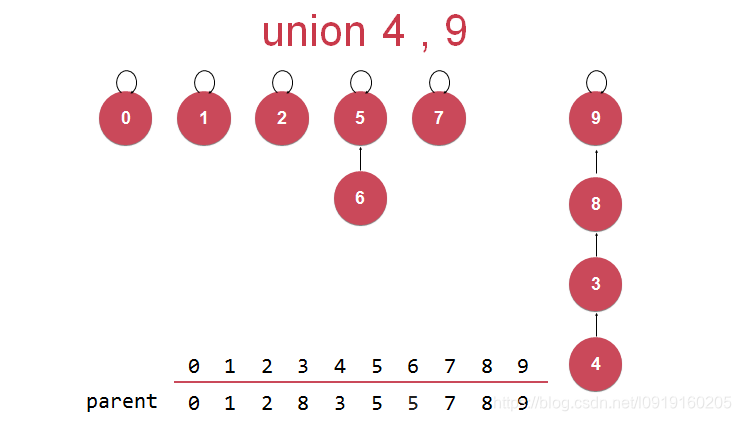
在这里插入图片描述
   这样会使并查集层数过大，降低查询效率。
   优化：每次合并时比较两个集合的元素数量，数量少的指向数量多的根节点。

代码如下：

// 我们的第三版Union-Find
namespace UF3{

    class UnionFind{

    private:
        int* parent; // parent[i]表示第i个元素所指向的父节点
        int* sz;     // sz[i]表示以i为根的集合中元素个数
        int count;   // 数据个数

    public:
        // 构造函数
        UnionFind(int count){
            parent = new int[count];
            sz = new int[count];
            this->count = count;
            for( int i = 0 ; i < count ; i ++ ){
                parent[i] = i;
                sz[i] = 1;//只有一个自身元素
            }
        }

        // 析构函数
        ~UnionFind(){
            delete[] parent;
            delete[] sz;
        }

        // 查找过程, 查找元素p所对应的集合编号
        // O(h)复杂度, h为树的高度
        int find(int p){
            assert( p >= 0 && p < count );
            // 不断去查询自己的父亲节点, 直到到达根节点
            // 根节点的特点: parent[p] == p
            while( p != parent[p] )
                p = parent[p];
            return p;
        }

        // 查看元素p和元素q是否所属一个集合
        // O(h)复杂度, h为树的高度
        bool isConnected( int p , int q ){
            return find(p) == find(q);
        }

        // 合并元素p和元素q所属的集合
        // O(h)复杂度, h为树的高度
        void unionElements(int p, int q){

            int pRoot = find(p);
            int qRoot = find(q);

            if( pRoot == qRoot )
                return;

            // 根据两个元素所在树的元素个数不同判断合并方向
            // 将元素个数少的集合合并到元素个数多的集合上
            if( sz[pRoot] < sz[qRoot] ){
                parent[pRoot] = qRoot;
                sz[qRoot] += sz[pRoot];
            }
            else{
                parent[qRoot] = pRoot;
                sz[pRoot] += sz[qRoot];
            }
        }
    };
}

   这种优化效果十分明显，比前两种实现效率要高出很多！

优化二：基于rank的优化

   下面的例子，如果要合并元素4和元素2，按照之前元素数量少的根指向元素数量多的根：
合并前：
在这里插入图片描述
合并后：
在这里插入图片描述
其实层数是增加的，优化：应当比较层数，层数少的根指向层数多的根，如下图：
在这里插入图片描述
设置一个rank[i]数组，rank[i]表示根节点为i的数的高度。

代码如下：

// 我们的第四版Union-Find
namespace UF4{

    class UnionFind{

    private:
        int* rank;   // rank[i]表示以i为根的集合所表示的树的层数
        int* parent; // parent[i]表示第i个元素所指向的父节点
        int count;   // 数据个数

    public:
        // 构造函数
        UnionFind(int count){
            parent = new int[count];
            rank = new int[count];
            this->count = count;
            for( int i = 0 ; i < count ; i ++ ){
                parent[i] = i;
                rank[i] = 1;//初始化元素层数为1层
            }
        }

        // 析构函数
        ~UnionFind(){
            delete[] parent;
            delete[] rank;
        }

        // 查找过程, 查找元素p所对应的集合编号
        // O(h)复杂度, h为树的高度
        int find(int p){
            assert( p >= 0 && p < count );
            // 不断去查询自己的父亲节点, 直到到达根节点
            // 根节点的特点: parent[p] == p
            while( p != parent[p] )
                p = parent[p];
            return p;
        }

        // 查看元素p和元素q是否所属一个集合
        // O(h)复杂度, h为树的高度
        bool isConnected( int p , int q ){
            return find(p) == find(q);
        }

        // 合并元素p和元素q所属的集合
        // O(h)复杂度, h为树的高度
        void unionElements(int p, int q){

            int pRoot = find(p);
            int qRoot = find(q);

            if( pRoot == qRoot )
                return;

            // 根据两个元素所在树的根元素对应的层数不同判断合并方向
            // 将元素层数少的集合合并到元素层数多的集合上
            if( rank[pRoot] < rank[qRoot] ){
                parent[pRoot] = qRoot;
            }
            else if( rank[qRoot] < rank[pRoot]){
                parent[qRoot] = pRoot;
            }
            else{ // rank[pRoot] == rank[qRoot]
                parent[pRoot] = qRoot;
                rank[qRoot] += 1;   // 此时, 我维护rank的值
            }
        }
    };
}

优化三：路径压缩

路径压缩1
   之前的优化都是在优化合并，其实查找操作也可以进行优化，可以在查找根节点的同时将层数变小。

操作：先查看要查找元素的父节点是不是根节点，如果不是就指向父节点的父节点，以此类推。
查找元素4所在集合过程如下：
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
只需要修改find函数：

// 查找过程, 查找元素p所对应的集合编号
// O(h)复杂度, h为树的高度
int find(int p){
    assert( p >= 0 && p < count );
    // 不断去查询自己的父亲节点, 直到到达根节点
    // 根节点的特点: parent[p] == p
    while( p != parent[p] )
        p = parent[p];
    return p;
}

路径压缩2
进行进一步优化，将所有子节点都指向根节点，如下图所示：
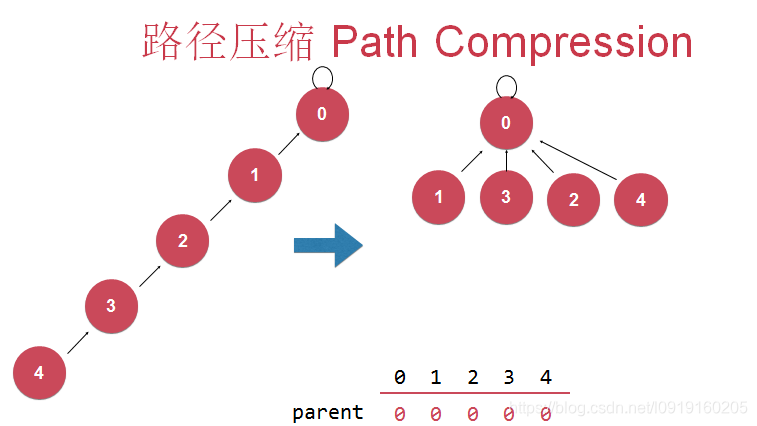
在这里插入图片描述
find函数代码：

// 查找过程, 查找元素p所对应的集合编号
// O(h)复杂度, h为树的高度
int find(int p){
    assert( p >= 0 && p < count );
    
    // path compression 2, 递归算法
    if( p != parent[p] )
        parent[p] = find( parent[p] );
    return parent[p];
}

第四版版Union-Find代码：
注意：这里rank在路径压缩过程中没有更新？？？

// 我们的第四版Union-Find
namespace UF4{

    class UnionFind{

    private:
        // rank[i]表示以i为根的集合所表示的树的层数
        // 在后续的代码中, 我们并不会维护rank的语意, 也就是rank的值在路径压缩的过程中, 有可能不在是树的层数值
        // 这也是我们的rank不叫height或者depth的原因, 他只是作为比较的一个标准
        int* rank;
        int* parent; // parent[i]表示第i个元素所指向的父节点
        int count;   // 数据个数

    public:
        // 构造函数
        UnionFind(int count){
            parent = new int[count];
            rank = new int[count];
            this->count = count;
            for( int i = 0 ; i < count ; i ++ ){
                parent[i] = i;
                rank[i] = 1;
            }
        }

        // 析构函数
        ~UnionFind(){
            delete[] parent;
            delete[] rank;
        }

        // 查找过程, 查找元素p所对应的集合编号
        // O(h)复杂度, h为树的高度
        int find(int p){
            assert( p >= 0 && p < count );

            // path compression 1
            while( p != parent[p] ){
                parent[p] = parent[parent[p]];
                p = parent[p];
            }
            return p;

            // path compression 2, 递归算法
//            if( p != parent[p] )
//                parent[p] = find( parent[p] );
//            return parent[p];
        }

        // 查看元素p和元素q是否所属一个集合
        // O(h)复杂度, h为树的高度
        bool isConnected( int p , int q ){
            return find(p) == find(q);
        }

        // 合并元素p和元素q所属的集合
        // O(h)复杂度, h为树的高度
        void unionElements(int p, int q){

            int pRoot = find(p);
            int qRoot = find(q);

            if( pRoot == qRoot )
                return;

            // 根据两个元素所在树的元素个数不同判断合并方向
            // 将元素个数少的集合合并到元素个数多的集合上
            if( rank[pRoot] < rank[qRoot] ){
                parent[pRoot] = qRoot;
            }
            else if( rank[qRoot] < rank[pRoot]){
                parent[qRoot] = pRoot;
            }
            else{ // rank[pRoot] == rank[qRoot]
                parent[pRoot] = qRoot;
                rank[qRoot] += 1;   // 此时, 我维护rank的值
            }
        }
    };
}

并查集的操作，时间复杂度几乎是O(1)

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值