SVD分解基于FPGA实现2

关于jacobi的基本原理网上资料很多，它求解正余弦值的方法是通过求解方程得来的。
![在这里插入图片描述](https://img-blog.csdnimg.cn/2020042208465886.png)
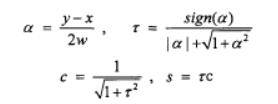
这样做可以方便求出正余弦值，但是不利于FPGA硬件实现，FPGA中可以用cordic算法求出反正切以及正余弦值，所以FPGA实现时应当使用arctan求出theta值，再直接算出正余弦结果，不用做任何乘除法就能得到结果。
由于我的整体最终是做盲源分离，所以我直接使用xilinx自带cordic ip核来求解，关于使用这些ip核的要点：
1.要知道FPGA中定点数的运算与小数点位置无关
2.arctan ip核求的结果不少arctan（x），而是arctan（y/x）
3.并且arctan（y/x）的值与y和x的大小无关，只与y与x的比值有关

因此，datasheet也指出了y和x的输入范围必须是-1到+1，不然会报错
4.所有求解我想要反正切值时，应当先对y和x做归一化，具体做法是比较y与x的绝对值大小，然后以较大的绝对值为基准做归一化处理
5.然而，如果这样做归一化，尽管可以使用移位除法器较快得到结果，但还是麻烦了。但是！！比如我的情况是，输入y和x都是32位定点数据，其中前后20位为小数位，但将数据ip核认为32位中后29位为小数位，我的数据之前做过归一化处理，所以这里我可以不做任何改动直接将y与x输入给ip核即可，注意输出结果32位，前三位是符号位和整数位