剑指offer 145. 一看就会的二叉树的后序遍历解法（递归与非递归）-优快云博客

本文链接：https://blog.youkuaiyun.com/kris_paul/article/details/118577893

本文详细介绍了如何实现二叉树的后序遍历，包括递归和非递归两种方法。在非递归解法中，通过分析错误的解法及死循环的原因，提出了解决方案。二叉树遍历在计算机科学中具有广泛的应用，如二叉搜索树、堆、表达式树和哈夫曼树等。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一看就会的二叉树的后序遍历解法（递归与非递归）

递归

能做非递归的没有不会递归的：

class Solution {
public:
    void traversal(TreeNode* cur,vector<int>& vec){
        if(cur==NULL){return ;}
        traversal(cur->left,vec);
        traversal(cur->right,vec);
        vec.push_back(cur->val);
    }
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root,result);
        return result;
    }
};

重点在于非递归

后序遍历与前序遍历、中序遍历有相似之处。
1.前序代码如下：

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> v;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        //cur不为空，表示还有树没有开始访问
        //st不为空，表示还有节点的右子树没有访问
        while(cur||!st.empty()){
            //1.访问并保存左路结点进栈
            while(cur){
                v.push_back(cur->val);
                st.push(cur);
                cur = cur->left;
            }
            //2.对于root这棵树，剩下的是左路节点的右子树没有访问
            //依次从栈里拿出来访问
            TreeNode* top = st.top();
            st.pop();
            //子问题走右树
            cur = top->right;
        }
        return v;
    }
};

以这样的二叉树为例，首次存放左边的部分：
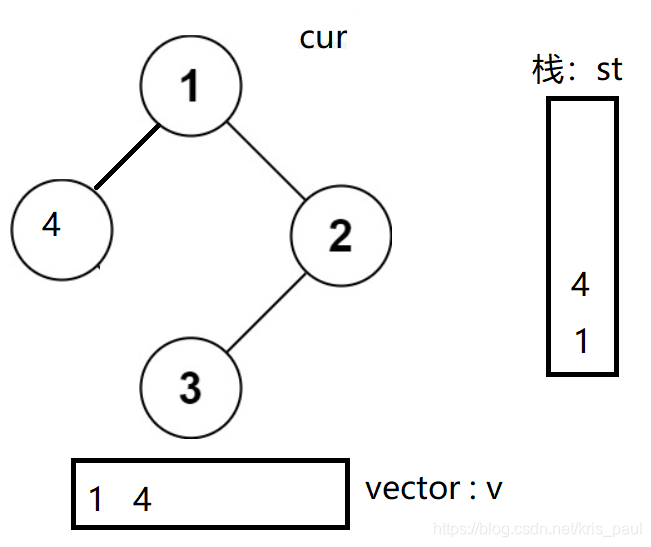
在这里插入图片描述
2.我们当前需要取出4、1，又因为1的右边有子树，所以转化为子问题。
按照前序、中序的惯性思维来修改，那么只需要把顺序改成左子树、右子树、根节点即可。我们加上判断右的代码。但前序、中序的代码简单改一改是行不通的：

//考虑不周的解
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> v;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while(cur||!st.empty()){
            while(cur){
                st.push(cur);
                cur = cur->left;
            }
            TreeNode* top = st.top();
            if(cur->right==nullptr){
                v.push_back(top->val);
                st.pop(); 
            }
            else{
                cur = cur->right;
            }
        }
        return v;
    }
};

3.此时会发生一种令人不解的情况，死循环
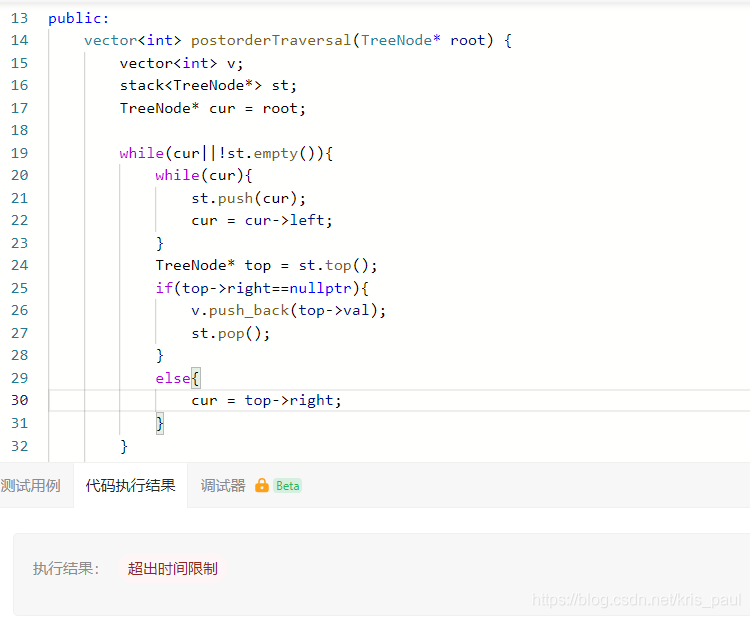
在这里插入图片描述
但当我修改测试用例为[4,1]后，代码通过

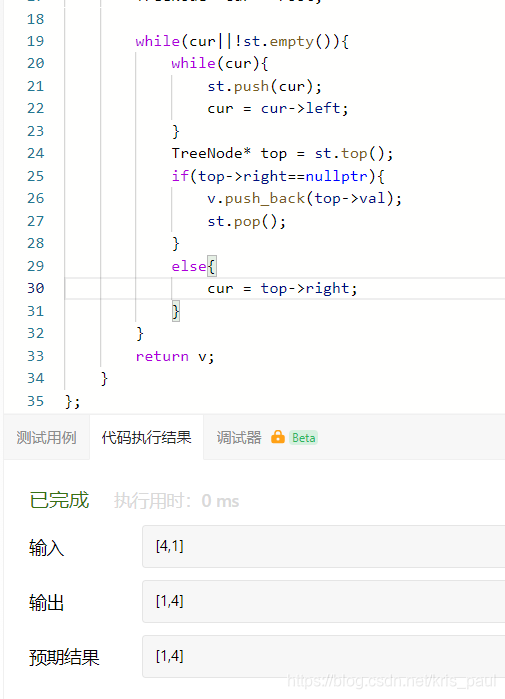
分析如下

当只有左子树的时候，没有暴露问题，但右子树出来后，问题随之而来

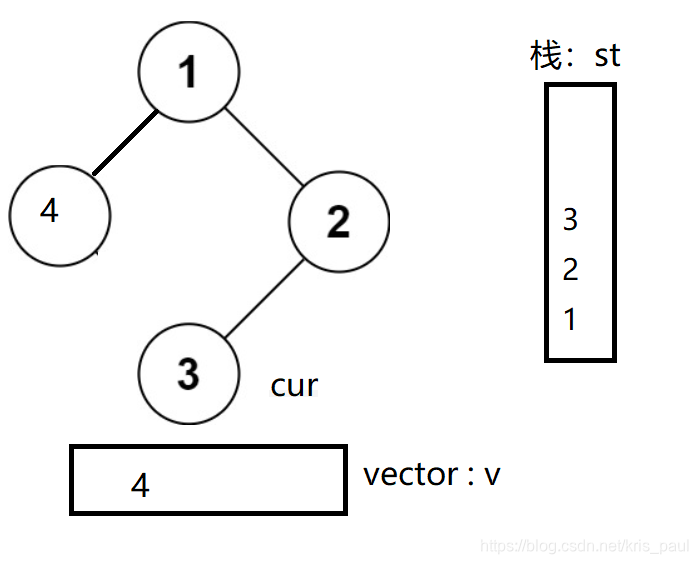
在这里插入图片描述
如图所示，在栈内部第一次访问1的时候，来到子问题，随后按照代码，从栈内一一出来，

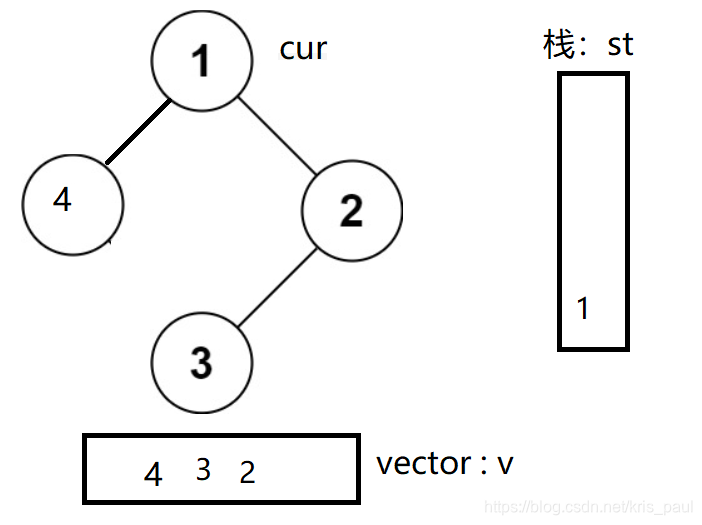
当cur第二次指向1的时候，通过判断语句：

if(cur->right==nullptr){
	v.push_back(top->val);
    st.pop(); 
}
else{
	cur = cur->right;
}

可以得出，cur又指向cur->right，所以会陷入死循环。

解决方式

找寻一个新的条件去判断出第二次访问右子树的时刻，结束循环。

我们可以通过计数的方式，记录vector内部存放的值，当最后一个结点的值与cur->right相等的时候，证明这是第二次访问的该结点。
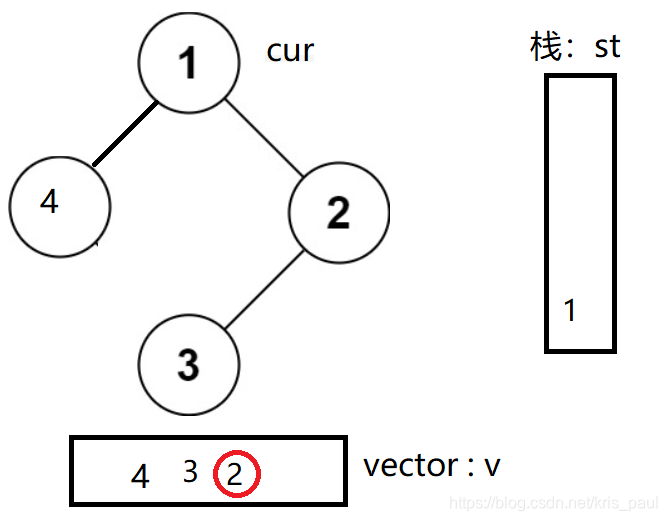
在这里插入图片描述

成功拿下

修改后的代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> v;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        TreeNode* prev = nullptr;
        while(cur||!st.empty()){
            while(cur){
                st.push(cur);
                cur = cur->left;
            }
            TreeNode* top = st.top();
            if(top->right==nullptr||top->right ==prev){
                v.push_back(top->val);
                prev = top;
                st.pop(); 
            }
            else{
                cur = top->right;
            }
        }
        return v;
    }
};

在这里插入图片描述

二叉树

二叉树（Binary Tree）是一种特殊的树形数据结构，它的每个节点最多有两个子节点，通常被称为左子节点和右子节点。二叉树在计算机科学中非常常见，因为它们具有简单、高效和易于实现的特点。

二叉树的基本性质

递归定义：二叉树由根节点、左子树和右子树组成，而左子树和右子树本身也是二叉树。
空树：二叉树可以是空的，此时没有节点。
度：一个二叉树节点的度是指其拥有的子节点数，二叉树的度最大为2。
深度：二叉树的深度（或高度）是从根节点到最远叶子节点的最长路径上的节点数。
满二叉树：每一层的节点数都达到最大值的二叉树称为满二叉树。即对于深度为k的满二叉树，总共有2^k - 1个节点。
完全二叉树：对于深度为k的，有n个节点的二叉树，当且仅当其每一个节点都与深度为k的满二叉树中编号从1至n的节点一一对应时称之为完全二叉树。

二叉树的表示

在计算机中，二叉树通常可以通过以下方式表示：

链式表示：每个节点都有一个指向其左子节点的指针，一个指向其右子节点的指针，以及一个数据域来存储节点的值。
数组表示：对于完全二叉树，可以使用数组来存储节点。对于非完全二叉树，也可以使用数组，但会浪费一些空间。

二叉树的遍历

遍历二叉树是指按照某种顺序访问树中的每个节点一次且仅一次。常见的遍历方式有：

前序遍历（Pre-order Traversal）：先访问根节点，然后遍历左子树，最后遍历右子树。
中序遍历（In-order Traversal）：先遍历左子树，然后访问根节点，最后遍历右子树。这种遍历方式常用于二叉搜索树。
后序遍历（Post-order Traversal）：先遍历左子树，然后遍历右子树，最后访问根节点。
层次遍历（Level-order Traversal）：从根节点开始，按层次从上到下、从左到右遍历节点。这通常需要使用队列来实现。

二叉树的应用

二叉树在计算机科学中有广泛的应用，包括但不限于：

二叉搜索树（Binary Search Tree, BST）：一种特殊的二叉树，它或者为空，或者满足以下性质：若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；任意节点的左、右子树也分别为二叉搜索树。二叉搜索树常用于实现高效的搜索和排序算法。
堆（Heap）：一种特殊的完全二叉树，通常用于实现优先队列。堆分为最大堆和最小堆，其中最大堆的父节点的值总是大于或等于其子节点的值，而最小堆的父节点的值总是小于或等于其子节点的值。
表达式树（Expression Tree）：用于表示数学表达式的一种二叉树。表达式树的叶子节点表示操作数，非叶子节点表示运算符。通过遍历表达式树，可以计算表达式的值。
哈夫曼树（Huffman Tree）：一种特殊的二叉树，常用于数据压缩中的霍夫曼编码。它根据字符的出现频率构建树，频率高的字符离根节点较远，频率低的字符离根节点较近。通过霍夫曼编码，可以用较短的编码表示频率高的字符，用较长的编码表示频率低的字符，从而实现数据压缩。