第八章——堆

小结

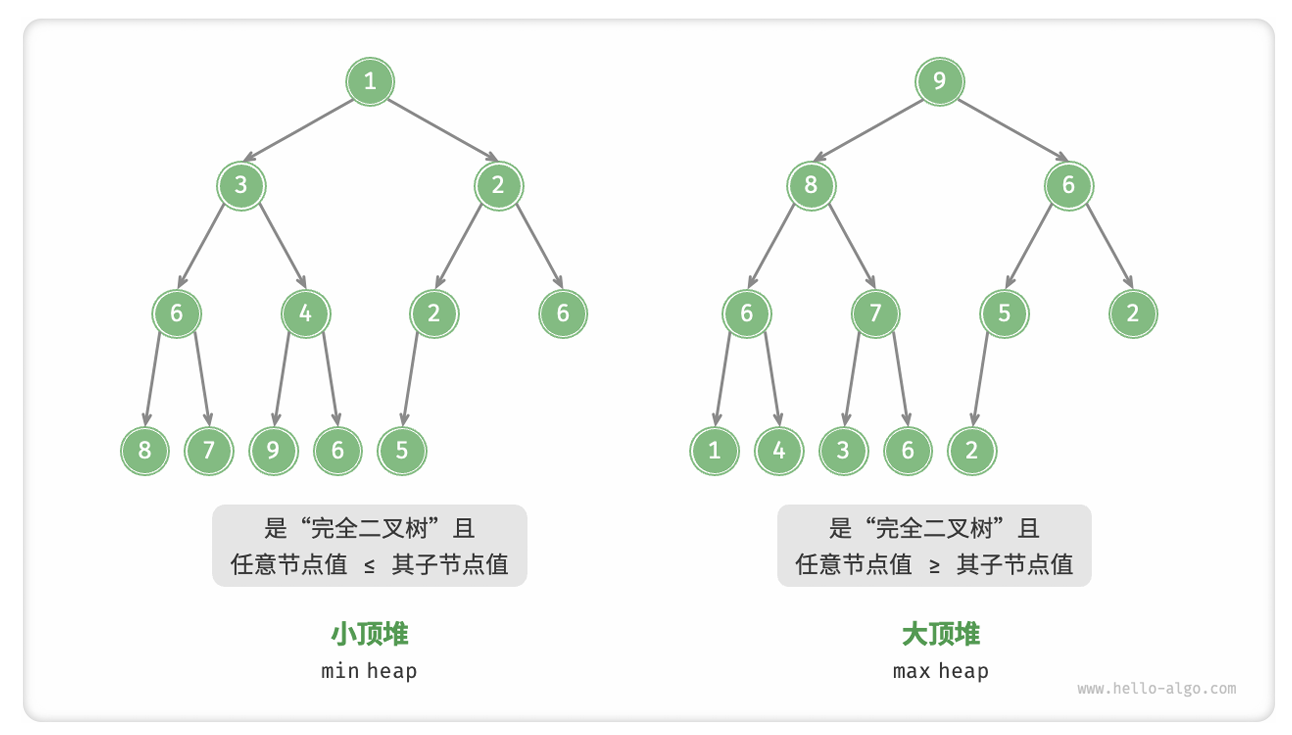
‧ 堆是一棵完全二叉树，根据成立条件可分为大顶堆和小顶堆。大（小）顶堆的堆顶元素是最大（小）的。

‧ 优先队列的定义是具有出队优先级的队列，通常使用堆来实现。

堆常见应用：

1）优先队列：堆通常作为实现优先队列的首选数据结构，其入队和出队操作的时间复杂度均为𝑂(log𝑛) ，而建队操作为𝑂(𝑛)，这些操作都非常高效。

2）堆排序：给定一组数据，我们可以用它们建立一个堆，然后不断地执行元素出堆操作，从而得到有序数据。

3）获取最大的𝑘个元素：这是一个经典的算法问题，同时也是一种典型应用，例如选择热度前10的新闻作为微博热搜，选取销量前10的商品等。

‧ 堆的常用操作及其对应的时间复杂度包括：元素入堆𝑂(log𝑛)、堆顶元素出堆𝑂(log𝑛)和访问堆顶元素𝑂(1)等。

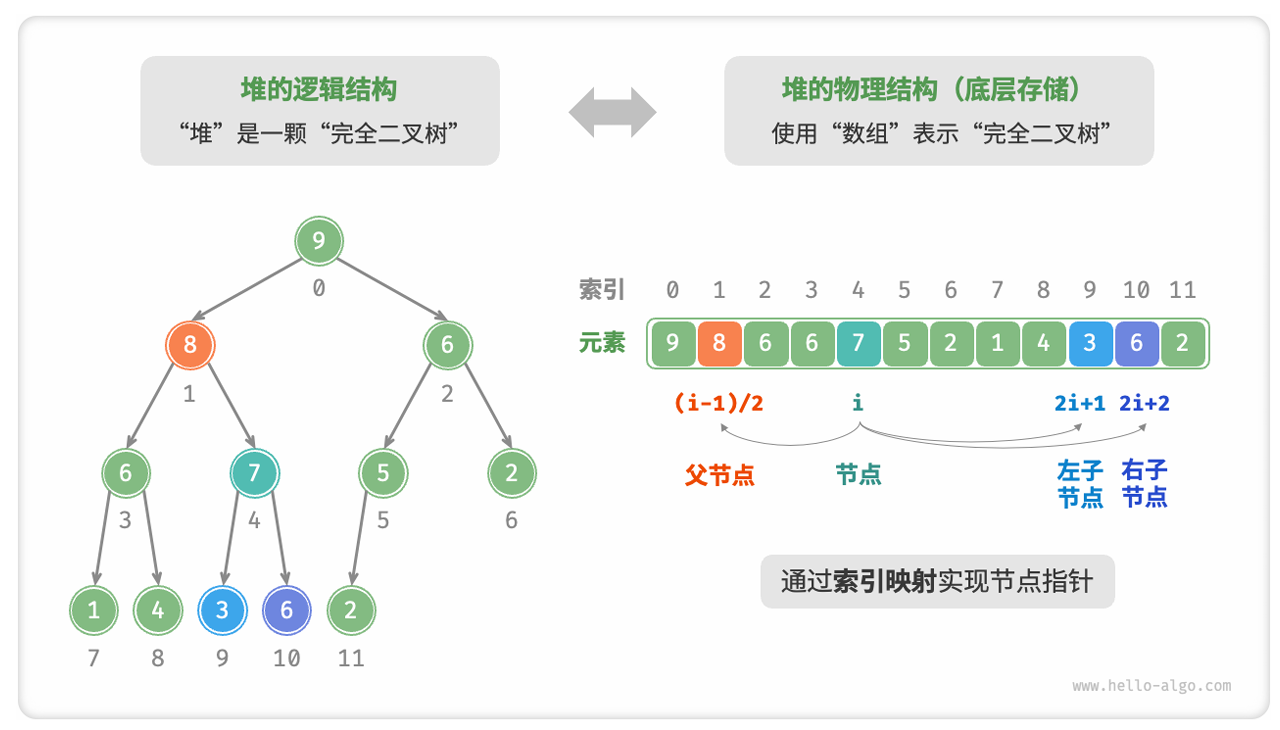
‧ 完全二叉树非常适合用数组表示，因此我们通常使用数组来存储堆。回顾完全二叉树的定义，None只出现在最底层且靠右的位置，因此所有None一定出现在层序遍历序列的末尾。这意味着使用数组表示完全二叉树时，可以省略存储所有None，非常方便。

‧ 堆化操作用于维护堆的性质，在入堆和出堆操作中都会用到。

堆化是“从顶至底”的，即比较当前节点和子节点，如果不符合堆性质，就交换，并继续向下检查，直到叶子节点或符合条件为止。

‧ 输入𝑛个元素并建堆的时间复杂度可以优化至𝑂(𝑛)，非常高效。

‧ 建堆操作——分为：1）自顶向下构建  2）自底向上构建

 

自底向上建堆步骤：

1. 将列表所有元素原封不动添加到堆中。

2. 倒序遍历堆（即层序遍历的倒序），依次对每个非叶节点执行“从顶至底堆化”。

• 自底向上建堆‌通过倒序处理非叶节点，利用子树已局部有序的特性，将时间复杂度优化到 ‌O(n)‌。
• 核心思想是‌从最底层开始逐步向上合并子树堆‌，减少重复调整次数。

‧ Top‑K是一个经典算法问题，可以使用堆数据结构高效解决，时间复杂度为𝑂(𝑛log𝑘)。

基于堆更加高效地解决Top‑K问题，流程如下所示：

1. 初始化一个小顶堆，其堆顶元素最小。

2. 先将数组的前𝑘个元素依次入堆。

3. 从第𝑘+1个元素开始，若当前元素大于堆顶元素，则将堆顶元素出堆，并将当前元素入堆。

4. 遍历完成后，堆中保存的就是最大的𝑘个元素。