Help Jimmy

"Help Jimmy"是在下图所示的场景上完成的游戏：

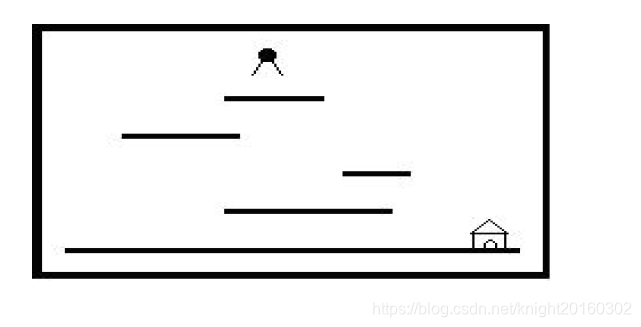
场景中包括多个长度和高度各不相同的平台。
地面是最低的平台，高度为零，长度无限。
Jimmy老鼠在时刻0从高于所有平台的某处开始下落，他的下落速度始终为1米/秒。
当Jimmy落到某个平台上时，游戏者选择让它向左跑还是向右跑，它跑动的速度也是
1米/秒。当Jimmy跑到平台边缘时，开始继续下落。Jimmy每次下落的高度不能超过MAX米，
不然就会摔死，游戏也会结束。
    设计一个程序，计算Jimmy到地面时可能的最早时间。

输入数据：
    第一行是测试数据的组数t(0<=t<=20)。每组测试数据的第一行是四个整数N,X,Y,MAX,用空格分隔。
    N是平台的数目(不包括地面)，X和Y是Jimmy开始下落的位置的横竖坐标，MAX是一次下落的最大高度。
    接下来的N行每行描述一个平台，包括三个整数，X1[i],X2[i]和H[i]。H[i]表示平台的高度。
    X1[i]和X2[i]表示平台左右端点的横坐标。1<=N<=1000,-2000<=X,X1[i],X2[i]<=2000,
    0<H[i]<Y<=20000(i=1..N)。所有坐标的单位都是米。
    Jimmy的大小和平台的厚度均忽略不计。如果Jimmy恰好落在某个平台的边缘，被视为落在平台上。
    所有的平台均不重叠或相连。测试数据保Jimmy一定能安全到达地面。

输出数据：
    对输入的每组测试数据，输出一个整数，Jimmy到地面时可能的最早时间。

输入样例：
    1
    3   8   17  20
    0   10  8   
    0   10  13
    4   14  3

输出样例：
    23

解题思路：
    Jimmy跳到一块板上后，可以有两种选择，向左走，或向右走。
    走到左端和走到右端所需的时间，是很容易算的。
    如果我们能知道，以左端为起点到达地面的最短时间，和以右端为起点到达地面的最短时间，那么向左走还是向右走，就很容易选择了。
    因此，整个问题就被分解成两个子问题，即Jimmy所在位置下方第一块板左端为起点到地面的最短时间，和右端为起点到地面的最短时间。
    这两个子问题在形式上和原问题是完全一致的。将板子从上到下从1开始进行无重复的编号（越高的板子编号越小，高度相同的几块板子，
    哪块编号在前无所谓），那么，和上面两个子问题相关的变量就只有板子的编号。

    不妨认为Jimmy开始的位置是一个编号为0，长度为0的板子，假设LeftMinTime(k)表示从k号板子左端到地面的最短时间，
    RightMinTime(k)表示从k号板子右端到地面的最短时间，那么，求板子k左端点到地面的最短时间的方法如下：
    if(板子k左端正下方没有别的板子){
        if(板子k的高度h(k)大于Max){
            LeftMinTime(k)=~;
        }else{
            LeftMinTime=h(k);
        }
    }else if(板子k左端正下方的板子编号是m){
        LeftMinTime(k)=h(k)-h(m)+Min(LeftMinTime(m)+Lx(k)-Lx(m),RightMinTime(m)+Rx(m)-Lx(k))
    }

    上面，h(i)就代表i号板子的高度，Lx(i)就代表i号板子左端点的横坐标，Rx(i)就代表i号板子右端点的横坐标。
    那么h(k)-h(m)当然就是从k号板子跳到m号板子所需要的时间，Lx(k)-Lx(m)就是从m号板子的落脚点走到m号板子左端点的时间，
    Rx(k)-Lx(k)就是从m号板子的落脚点走到右端点所需的时间。
    求RightMinTime(k)的过程类似。
    不妨认为Jimmy开始的位置是一个编号为0，长度为0的板子，那么整个问题LeftMinTime(0)。
    输入数据中，板子并没有按高度排序，所以程序中一定要首先将板子排序。

    时间复杂度：
        一共n个板子，每个左右两端的最小时间各算一次O(n)
        找出板子一段到地面之间有那块板子，需要遍历板子O(n)
        总的时间复杂度O(n^2)

 

#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<cmath>
#include<string.h>
const int N=1003;
const int M=20004;
const int INF=0x3f3f3f;
using namespace std;
struct Time{
    int x1,x2,h;
}a[N];
int dp[N][2]; //0表示第i的木板左边到底最短的时间  1表示右边的时间
int max_h,n;
int cmp(Time c,Time b)
{
    return c.h>b.h;//从大到小排列
}
void left(int i)//左
{
    int k=i+1;
    while(k<n+1&&a[i].h-a[k].h<=max_h)
    {
        if(a[i].x1>=a[k].x1&&a[i].x1<=a[k].x2)
        {
            dp[i][0]=a[i].h-a[k].h+min(dp[k][0]+a[i].x1-a[k].x1,dp[k][1]+a[k].x2-a[i].x1);
            return;
        }
        k++;
    }
    if(a[i].h-a[k].h>max_h)//不能到达下一平台
        dp[i][0]=INF;
    else
        dp[i][0]=a[i].h;//直接落地
    return;
}
void right(int i)//右
{
    int k=i+1;
    while(k<n+1&&a[i].h-a[k].h<=max_h)
    {
        if(a[i].x2>=a[k].x1&&a[i].x2<=a[k].x2)
        {
            dp[i][1]=a[i].h-a[k].h+min(dp[k][0]+a[i].x2-a[k].x1,dp[k][1]+a[k].x2-a[i].x2);
            return;
        }
        k++;
    }
    if(a[i].h-a[k].h>max_h)//不能到达下一平台
        dp[i][1]=INF;
    else//直接落地
        dp[i][1]=a[i].h;
    return;
}
int main()
{
    int t,x,y,i;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d%d%d",&n,&x,&y,&max_h);
        a[0].x1=-20000;
        a[0].x2=20000;
        a[0].h=0;
        a[1].x1=a[1].x2=x;
        a[1].h=y;
        for(i=2;i<=n+1;i++)
            scanf("%d%d%d",&a[i].x1,&a[i].x2,&a[i].h);
        sort(a,a+n+2,cmp);
        memset(dp,0,sizeof(dp));
        for(i=n;i>=0;i--)
        {
            left(i);//进行左
            right(i);//进行右
        }
        int time=min(dp[0][0],dp[0][1]);
        printf("%d\n",time);
    }
    return 0;
}

参考：https://blog.youkuaiyun.com/qq_37605573/article/details/77366536

https://www.cnblogs.com/Renyi-Fan/p/6960829.html