文章介绍了傅里叶神经算子（FNO），这是一种在傅立叶空间中对积分内核进行参数化的新型神经网络运算符，用于高效且具有表现力的架构。FNO在Burgers方程、Darcy流和Navier-Stokes方程等的求解中表现出优越性能，速度比传统方法快三个数量级。代码示例展示了1D和2DFourier层的实现以及如何在FNO网络中使用它们。
一、源码和论文
二、论文解读
原理介绍
在这项工作中，我们通过直接在傅立叶空间中对积分内核进行参数化，从而制定了一种新的神经元运算符，从而实现了高效而富有表现力的体系结构。我们对Burgers方程，Darcy流和Navier-Stokes方程（包括湍流状态）进行实验。与现有的神经网络方法相比，我们的傅里叶神经算子显示了最先进的性能，并且与传统的PDE求解器相比，它的速度提高了三个数量级。
FNO的图解如下
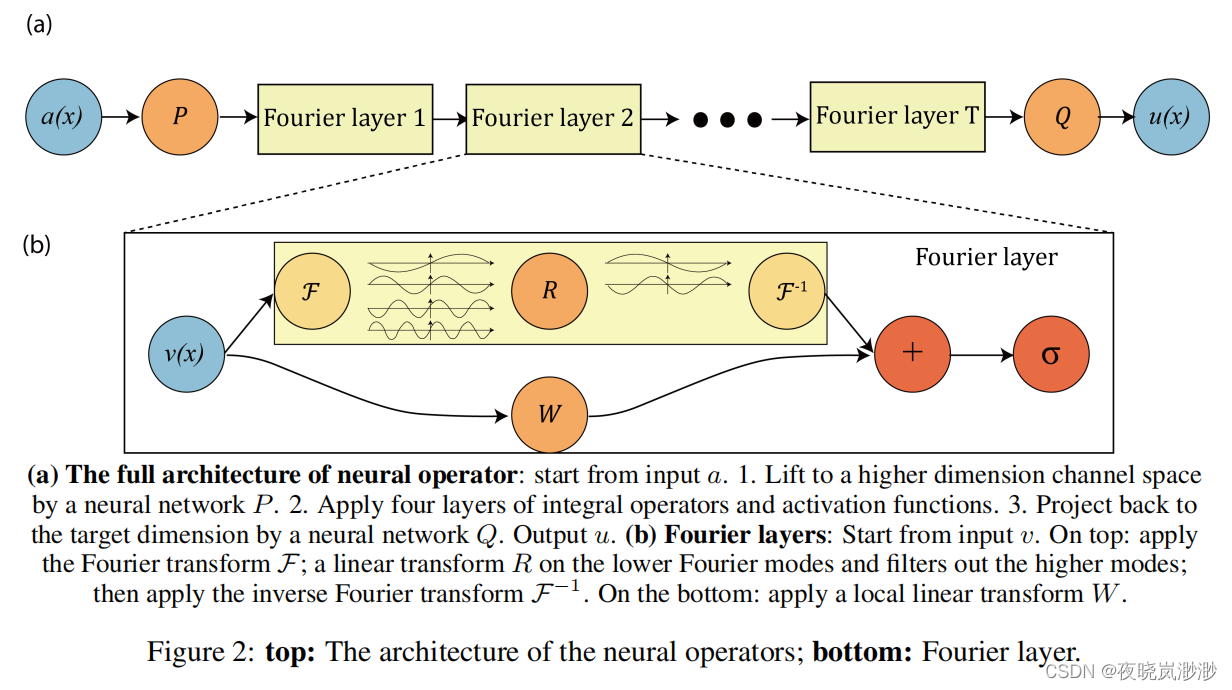
FNO的迭代格式如下:
核函数定义如下：
三、代码解读
一维和二维 Fourier layer 的实现如下:
################################################################
# 1d fourier layer
################################################################
class SpectralConv1d(tn.Module):
def __init__(self, in_channels, out_channels, modes1):
super(SpectralConv1d, self).__init__()
"""
1D Fourier layer. It does FFT, linear transform, and Inverse FFT.
"""
self.in_channels = in_channels
self.out_channels = out_channels
self.modes1 = modes1 # Number of Fourier modes to multiply, at most floor(N/2) + 1
self.scale = (1 / (in_channels*out_channels))
self.weights1 = tn.Parameter(self.scale * torch.rand(in_channels, out_channels, self.modes1, dtype=torch.cfloat))
# Complex multiplication
def compl_mul1d(self, input, weights):
# (batch, in_channel, x ), (in_channel, out_channel, x) -> (batch, out_channel, x)
return torch.einsum("bix,iox->box", input, weights)
def forward(self, x):
batchsize = x.shape[0]
# Compute Fourier coeffcients up to factor of e^(- something constant)
x_ft = torch.fft.rfft(x)
# Multiply relevant Fourier modes
out_ft = torch.zeros(batchsize, self.out_channels, x.size(-1)//2 + 1, device=x.device, dtype=torch.cfloat)
out_ft[:, :, :self.modes1] = self.compl_mul1d(x_ft[:, :, :self.modes1], self.weights1)
# Return to physical space
x = torch.fft.irfft(out_ft, n=x.size(-1))
return x
################################################################
# 2d fourier layer
################################################################
class SpectralConv2d(tn.Module):
def __init__(self, in_channels, out_channels, modes1, modes2):
super(SpectralConv2d, self).__init__()
"""
2D Fourier layer. It does FFT, linear transform, and Inverse FFT.
"""
self.in_channels = in_channels
self.out_channels = out_channels
self.modes1 = modes1 # Number of Fourier modes to multiply, at most floor(N/2) + 1
self.modes2 = modes2
self.scale = (1 / (in_channels * out_channels))
self.weights1 = tn.Parameter(self.scale * torch.rand(in_channels, out_channels, self.modes1, self.modes2, dtype=torch.cfloat))
self.weights2 = tn.Parameter(self.scale * torch.rand(in_channels, out_channels, self.modes1, self.modes2, dtype=torch.cfloat))
# Complex multiplication
def compl_mul2d(self, input, weights):
# (batch, in_channel, x,y ), (in_channel, out_channel, x,y) -> (batch, out_channel, x,y)
return torch.einsum("bixy,ioxy->boxy", input, weights)
def forward(self, x):
batchsize = x.shape[0]
# Compute Fourier coeffcients up to factor of e^(- something constant)
x_ft = torch.fft.rfft2(x)
# Multiply relevant Fourier modes
out_ft = torch.zeros(batchsize, self.out_channels, x.size(-2), x.size(-1)//2 + 1, dtype=torch.cfloat, device=x.device)
out_ft[:, :, :self.modes1, :self.modes2] = \
self.compl_mul2d(x_ft[:, :, :self.modes1, :self.modes2], self.weights1)
out_ft[:, :, -self.modes1:, :self.modes2] = \
self.compl_mul2d(x_ft[:, :, -self.modes1:, :self.modes2], self.weights2)
# Return to physical space
x = torch.fft.irfft2(out_ft, s=(x.size(-2), x.size(-1)))
return x
一维Fourier layer的使用
class FNO1d(tn.Module):
def __init__(self, modes, width):
super(FNO1d, self).__init__()
"""
The overall network. It contains 4 layers of the Fourier layer.
1. Lift the input to the desire channel dimension by self.fc0 .
2. 4 layers of the integral operators u' = (W + K)(u).
W defined by self.w; K defined by self.conv .
3. Project from the channel space to the output space by self.fc1 and self.fc2 .
input: the solution of the initial condition and location (a(x), x)
input shape: (batchsize, x=s, c=2)
output: the solution of a later timestep
output shape: (batchsize, x=s, c=1)
"""
self.modes1 = modes
self.width = width
self.padding = 2 # pad the domain if input is non-periodic
self.fc0 = tn.Linear(2, self.width) # input channel is 2: (a(x), x)
self.conv0 = SpectralConv1d(self.width, self.width, self.modes1)
self.conv1 = SpectralConv1d(self.width, self.width, self.modes1)
self.conv2 = SpectralConv1d(self.width, self.width, self.modes1)
self.conv3 = SpectralConv1d(self.width, self.width, self.modes1)
# 这里需要说明一下：nn.linear 和 kernel=1 的 Conv1d 是不同的.在FNO中, 由于最后两个维度需要倒换，所以使用卷积操作进行数据的更新
self.w0 = tn.Conv1d(self.width, self.width, 1)
self.w1 = tn.Conv1d(self.width, self.width, 1)
self.w2 = tn.Conv1d(self.width, self.width, 1)
self.w3 = tn.Conv1d(self.width, self.width, 1)
self.fc1 = tn.Linear(self.width, 128)
self.fc2 = tn.Linear(128, 1)
def forward(self, x):
grid = self.get_grid(x.shape, x.device) #得到网格点
x = torch.cat((x, grid), dim=-1) # 系数和网格点连接
x = self.fc0(x) # 使用全连接层，将输入数据变换到高维空间
x = x.permute(0, 2, 1) # [B,N,D]--->[B,D,N],为了适配傅里叶变换操作元素
# x = tnf.pad(x, [0,self.padding]) # pad the domain if input is non-periodic
x1 = self.conv0(x) # 第一个 FFT-->R--->IFFT
x2 = self.w0(x) # 第一个线性变换
x = x1 + x2 # x' = Wx + K(x,y)x
x = tnf.gelu(x) # sigma(x')
x1 = self.conv1(x)
x2 = self.w1(x)
x = x1 + x2
x = tnf.gelu(x)
x1 = self.conv2(x)
x2 = self.w2(x)
x = x1 + x2
x = tnf.gelu(x)
x1 = self.conv3(x)
x2 = self.w3(x)
x = x1 + x2
# x = x[..., :-self.padding] # pad the domain if input is non-periodic
x = x.permute(0, 2, 1)
# 使用全连接层，将Fourier变换到目标维度
x = self.fc1(x)
x = tnf.gelu(x)
x = self.fc2(x)
return x
def get_grid(self, shape, device):
batchsize, size_x = shape[0], shape[1]
gridx = torch.tensor(np.linspace(0, 1, size_x), dtype=torch.float)
gridx = gridx.reshape(1, size_x, 1).repeat([batchsize, 1, 1])
return gridx.to(device)
二维Fourier layer 的使用
class FNO2d(tn.Module):
def __init__(self, modes1, modes2, width):
super(FNO2d, self).__init__()
"""
The overall network. It contains 4 layers of the Fourier layer.
1. Lift the input to the desire channel dimension by self.fc0 .
2. 4 layers of the integral operators u' = (W + K)(u).
W defined by self.w; K defined by self.conv .
3. Project from the channel space to the output space by self.fc1 and self.fc2 .
input: the solution of the coefficient function and locations (a(x, y), x, y)
input shape: (batchsize, x=s, y=s, c=3)
output: the solution
output shape: (batchsize, x=s, y=s, c=1)
"""
self.modes1 = modes1
self.modes2 = modes2
self.width = width
self.padding = 9 # pad the domain if input is non-periodic
self.fc0 = tn.Linear(3, self.width) # input channel is 3: (a(x, y), x, y)
self.conv0 = SpectralConv2d(self.width, self.width, self.modes1, self.modes2)
self.conv1 = SpectralConv2d(self.width, self.width, self.modes1, self.modes2)
self.conv2 = SpectralConv2d(self.width, self.width, self.modes1, self.modes2)
self.conv3 = SpectralConv2d(self.width, self.width, self.modes1, self.modes2)
self.w0 = tn.Conv2d(self.width, self.width, 1)
self.w1 = tn.Conv2d(self.width, self.width, 1)
self.w2 = tn.Conv2d(self.width, self.width, 1)
self.w3 = tn.Conv2d(self.width, self.width, 1)
self.fc1 = tn.Linear(self.width, 128)
self.fc2 = tn.Linear(128, 1)
def forward(self, x):
grid = self.get_grid(x.shape, x.device) # [B, s, s, 2]
x = torch.cat((x, grid), dim=-1) # [B, s, s, 3]
x = self.fc0(x) # B, s, s, 32]
x = x.permute(0, 3, 1, 2) # [B, 32, s, s]
x = tnf.pad(x, [0, self.padding, 0, self.padding]) # [B, 32, s', s']
x1 = self.conv0(x)
x2 = self.w0(x)
x = x1 + x2
x = tnf.gelu(x)
x1 = self.conv1(x)
x2 = self.w1(x)
x = x1 + x2
x = tnf.gelu(x)
x1 = self.conv2(x)
x2 = self.w2(x)
x = x1 + x2
x = tnf.gelu(x)
x1 = self.conv3(x)
x2 = self.w3(x)
x = x1 + x2
x = x[..., :-self.padding, :-self.padding]
x = x.permute(0, 2, 3, 1)
x = self.fc1(x)
x = tnf.gelu(x)
x = self.fc2(x)
return x
def get_grid(self, shape, device):
batchsize, size_x, size_y = shape[0], shape[1], shape[2]
gridx = torch.tensor(np.linspace(0, 1, size_x), dtype=torch.float)
gridx = gridx.reshape(1, size_x, 1, 1).repeat([batchsize, 1, size_y, 1])
gridy = torch.tensor(np.linspace(0, 1, size_y), dtype=torch.float)
gridy = gridy.reshape(1, 1, size_y, 1).repeat([batchsize, size_x, 1, 1])
return torch.cat((gridx, gridy), dim=-1).to(device)
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
