统计学习方法|决策树

1 决策树

下面主要介绍决策树的基本概念，然后通过ID3和C4.5介绍特征的选择、决策树的生成以及决策树的修剪，最后介绍CART算法。

1.1 决策树模型与学习

1.1.1 决策树模型

  分类决策树模型是一种描述对实例进行分类的树形结构，决策树由结点 (node) 和有向边 (directed edge) 组成.结点两种类型:内部结点(internal node)和叶结点(1eaf node)内部结点表示一个特征或属性，叶结点表示一个类。
  用决策树分类，从根结点开始，对实例的某一特征进行测试，根据测试结果，将实例分配到其子结点；这时，每一个子结点对应着该特征的一个取值如此递归地对实例进行测试并分配，直至达到叶结点。最后将实例分到叶结点的类中。
  图5.1 是一个决策树的示意图。图中圆和方框分别表示内部结点和叶节点。

1.1.2 决策树与if-then规则

  可以将决策树看成一个if-then规则的集合。将决策树转换成if-then规则的过程是这样的：由决策树的根结点到叶结点的每一条路径构建一条规则；路径上内部结点的特征对应着规则的条件，而叶结点的类对应着规则的结论。决策树的路径或其对应的if-then规则集合具有一个重要的性质：互斥并且完备。这就是说，每个实例都被一条路径或一条规则所覆盖，而且只被一条路径或一条规则所覆盖。这里所谓覆盖是指实例的特征与路径上的特征一致或实例满足规则的条件。

1.1.3 决策树与条件概率分布

  决策树还表示给定特征条件下类的条件概率分布。这一条件概率分布定义在特征空间的一个划分（partition）上。将特征空间划分为互不相交的单元(cell)或区域 (region) ，并在每个单元定义一个类的概率分布就构成了一个条件概率分布。决策树的一条路径对应于划分中的个单元。决策树所表示的条件概率分布由各个单元给定条件下类的条件概率分布组成。假设X为表示特征的随机变量，Y为表示类的随机变量，那么这个条件概率分布可以表示为 P(Y，X)。X取值于给定划分下单元的集合.Y取值于类的集合，各叶结点(单元)上的条件概率往往偏向某一个类。即属于某 类的概率较大。决策树分类时将该结点的实例强行分到条件概率大的那一类去。


  上图a示意的表示了特征空间的一个划分。图中的大正方形表示特征空间。这个大正方形被若干个小矩形分割，每个小矩形表示一个单元。特征空间划分上的单元构成了一个集体，X取值为单元的集合。为简单起见，假设只有两类：正类和负类，即Y取值为+1和-1。小矩形中的数字表示单元的类。图b示意的表示特征空间划分确定时，特征（单元）给定条件下类的条件概率分布。图b中条件概率分布对应于图b的划分。当某个单元c的条件概率满足P(Y=+1|X=c)>0.5 时，则认为这个单元属于正类，即落在这个单元的实例都被视为正例图c为对应于图b中条件概率分布的决策树。

1.1.4 决策树学习

   决策树学习本质上是从训练数据集中归纳出一组分类规则。与训练数据集不相矛盾的决策树(即能对训练数据进行正确分类的决策树)可能有多个，也可能一个也没有。我们需要的是一个与训练数据矛盾较小的决策树，同时具有很好的泛化能力，从另一个角度看，决策树学习是由训练数据集估计条件概率模型。基于特征空间划分的类的条件概率模型有无穷多个。我们选择的条件概率模型应该不仅对训练数据有很好的拟合而且对未知数据有很好的预测。
   决策树学习用损失函数表示这一目标。如下所述，决策树学习的损失函数通常是正则化的极大似然函数。决策树学习的策略是以损失函数为目标函数的最小化。
   当损失函数确定以后，学习问题就变为在损失函数意义下选择最优决策树的问题。因为从所有可能的决策树中选取最优决策树是 NP 完全问题，所以现实中决策树学习算法通常采用启发式方法，近似求解这一最优化问题。这样得到的决策树是次最优 (sub-optimal)的。
   决策树学习的算法通常是一个递归地选择最优特征，并根据该特征对训练数掘进行分割，使得对各个子数据集有一个最好的分类的过程。这一过程对应着对特征空间的划分，也对应着决策树的构建。开始，构建根结点，将所有训练数据都放在根结点选择一个最优特征，按照这一特征将训练数据集分割成子集，使得各个于集有一个在当前条件下最好的分类。如果这些子集已经能够被基本正确分类，那么构建叶结点，并将这些子集分到所对应的叶结点中去。如果还有子集不能被基本正确分类，那么就对这些子集选择新的最优特征，继续对其进行分割，构建相应的结点。如此递归地进行下去，直至所有训练数据子集被基本正确分类，或者没有合适的特征为止。最后每个子集都被分到叶结点上，即都有了明确的类这就生成了一棵决策树。
   以上方法生成的决策树可能对训练数据有很好的分类能力，但对未知的测试数据却未必有很好的分类能力，即可能发生过拟合现象。我们需要对己生成的树自下而上进行剪枝，将树变得更简单，从而使它具有更好的泛化能力。具体地，就是去掉过于细分的叶结点，使其回返到父结点，甚至更高的结点，然后将父结点或更高的结点改为新的叶结点。
   如果特征数量很多，也可以在决策树学习开始的时候，对特征进行选择，只留下对训练数据有足够分类能力的特征。
   可以看出，决策树学习算法包含特征选择、决策树的生成与决策树的剪枝过程。由于决策树表示一个条件概率分布，所以深浅不同的决策树对应着不同复杂度的概率模型。决策树的生成对应于模型的局部选择，决策树的剪枝对应于模型的全局选择.决策树的生成只考虑局部最优。相对地，决策树的剪枝则考虑全局最优。决策树学习常用的算法有ID3 、C4.5与 CART， 下面结合这些算法分别叙述决策树学习的特征选择、决策树的生成和剪枝过程。

1.2 特征选择

   特征选择在于选取对训练数据具有分类能力的特征。这样可以提高决策树学习的效率.如果利用一个特征进行分类的结果与随机分类的结果没有很大差别，则称这个特征是没有分类能力的。经验上扔掉这样的特征对决策树学习的精度影响不大。通常特征选择的准则是信息增益或信息增益比。

1.2.1信息增益

为了便于说明，先给出煽 条件娟的定义：

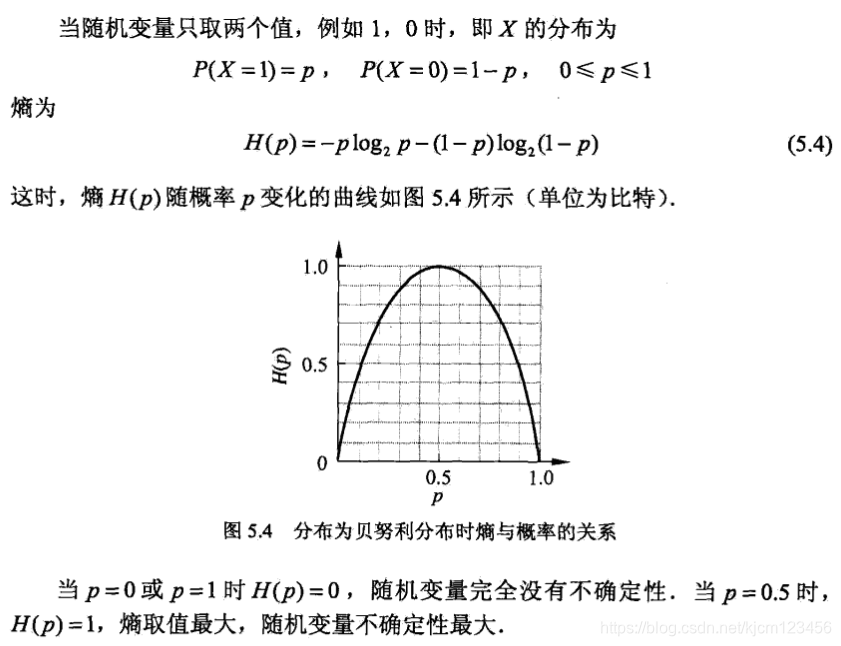
1.2.3 信息增益比

  信息增益值的大小是相对于训练数据集而言的，并没有绝对意义。在分类问题困难时，也就是说在训练数据集的经验熵大的时候，信息增益值会偏大。反之，信息增益值会偏小。使用信息增益比( information gain ratio) 可以对这一问题进行校正。这是特征选择的另一准则。

1.3决策树的生成

1.3.1 ID3算法

  ID3算法的核心是在决策树各个结点上应用信息增益准则选择特征，递归地构建决策树。具体方法是：从根结点（root node）开始，对结点计算所有可能的特征的信息增益，选择信息增益握大的特征作为结点的特征，由该特征的不同取值建立于结点；再对子结点递归地调用以上方法，构建决策树；直到所有特征的信息增益均很小或没有特征可以选择为止。最后得到一个决策树。ID3 相当于用极大似然法进行概率模型的选择。

1.4 决策树的剪枝

  决策树生成算法递归地产生决策树，直到不能继续下去为止这样产生的树往往对训练数据的分类很准确，但对未知的测试数据的分类却没有那么准确，即出现过拟告现象。过拟合的原因在于学习时过多地考虑如何提高对训练数据的正确分类，从而构建出过于复杂的决策树解决这个问题的办法是考虑诀策树的复杂度，对己生成的决策树进行简化.
  在决策树学习中将己生成的树进行简化的过程称为剪枝 (prun Íßg). 具体地、剪枝从己生成的树上载掉 些子树或叶结点，并将其根结点就父结点作为新的叶结点，从而简化分类树模型。
下面介绍一种简单的决策树学习的剪枝算法。

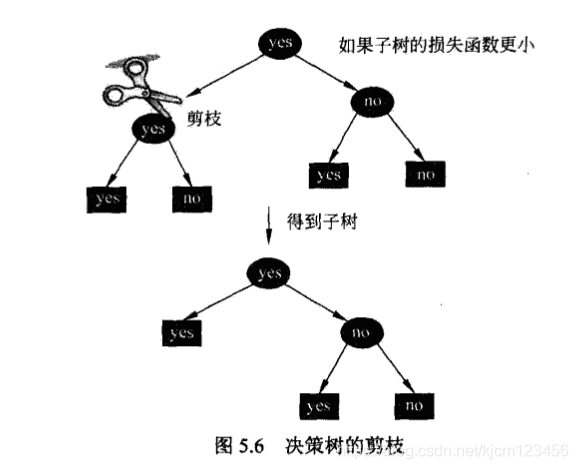
1.5 CART算法

1.5.1 CART生成

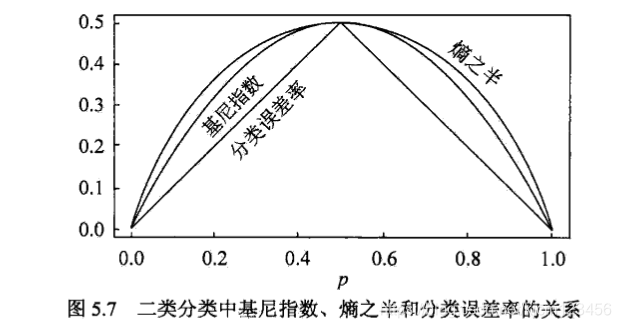
1.5.2 CART剪枝

现在写出CART剪枝的算法：