完全背包 排列

完全背包排列，为什么先排列物品再遍历背包就可以做到排列了？想不出来手动尝试一下吧。

先以手动推导dp[3][5]为例子

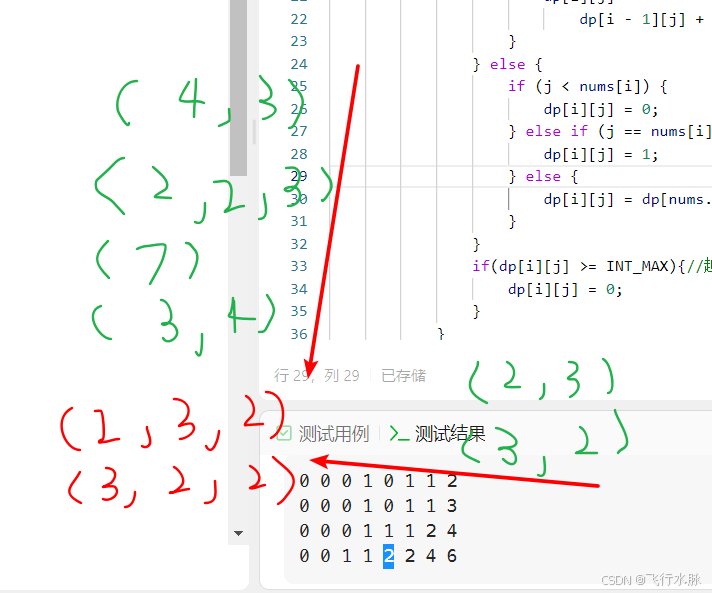
本列方向可以看到先是3和2去合成(2,3)

本行方向则是2和3去合成(3,2)

使结果包含了(2,3)与(3,2)

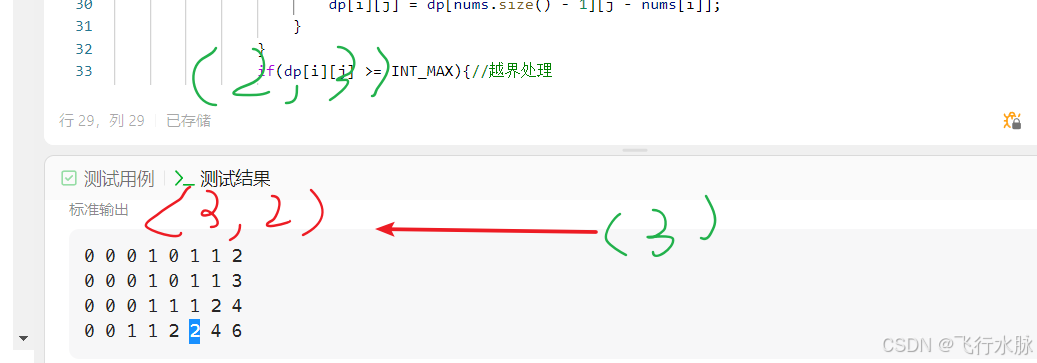
再以手动推导dp[3][7]为例子（这里标蓝标错了，可以忽略）

本行方向上可以看到3与4合成(4,3)和(2,2,3)[这里合成为4的集合包含(4)和(2,2)]

                                7单独合成(7)

                                4和3合成(4,3)[这里合成3的集合仅包含(3)]

本列方向上2与5合成(2,3,2)和(3,2,2)[合成5的集合包含(2,3)(3,2)]

可以看到dp[0][7]实际上并不满足dp[i][j]的含义,但是保证了dp[3][7]一定满足dp[i][j]的含义使得返回结果是正确的。

可以看到最终结果中同时存在(2,2,3)(2,3,2)(3,2,2)，这是因为先遍历物品再遍历背包使得后面的物品也可以参与前面的合成例如dp[0][5]的合成使得(2,3)可以存在，如果采用先遍历背包再遍历物品则永远只能得出(3,2).

这是题目 377. 组合总和 Ⅳ

. - 力扣（LeetCode）

这是代码

class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        // 1.dp[i][j]的含义：0~i数字装满容量为j的背包有几种方法(排列
        // [1,2][2,1]视为不同方法)
        vector<vector<long long>> dp(nums.size(), vector<long long>(target + 1, 0));

        // 3.初始化dp数组
        dp[0][0] = 0; // 题目target步包含0，可以认为不放元素不作为一种方法

        // 4.递推顺序
        for (int j = 1; j <= target; j++) {
            for (int i = 0; i < nums.size(); i++) {
                if (i >= 1) {
                    if (j < nums[i]) {
                        dp[i][j] = dp[i - 1][j];
                    } else if (j == nums[i]) {
                        dp[i][j] = dp[i - 1][j] + 1;
                    } else {
                        // 2.递推顺序
                        dp[i][j] =
                            dp[i - 1][j] + dp[nums.size() - 1][j - nums[i]];
                    }
                } else {
                    if (j < nums[i]) {
                        dp[i][j] = 0;
                    } else if (j == nums[i]) {
                        dp[i][j] = 1;
                    } else {
                        dp[i][j] = dp[nums.size() - 1][j - nums[i]];
                    }
                }
                if(dp[i][j] >= INT_MAX){//越界处理
                    dp[i][j] = 0;
                }
            }
        }

        // 5.打印dp数组
        for (int i = 0; i < nums.size(); i++) {
            for (int j = 0; j <= target; j++) {
                std::cout << dp[i][j] << " ";
            }
            std::cout << std::endl;
        }
        return dp[nums.size() - 1][target];
    }
};