洛谷题（栈，接水，约瑟夫）

栈

今天写了三道题，其中两道题的解法使用的是栈，之前也没学过栈的知识点，靠今天写题目学习了一些，一边解题一边总结，如下。

第一个栈问题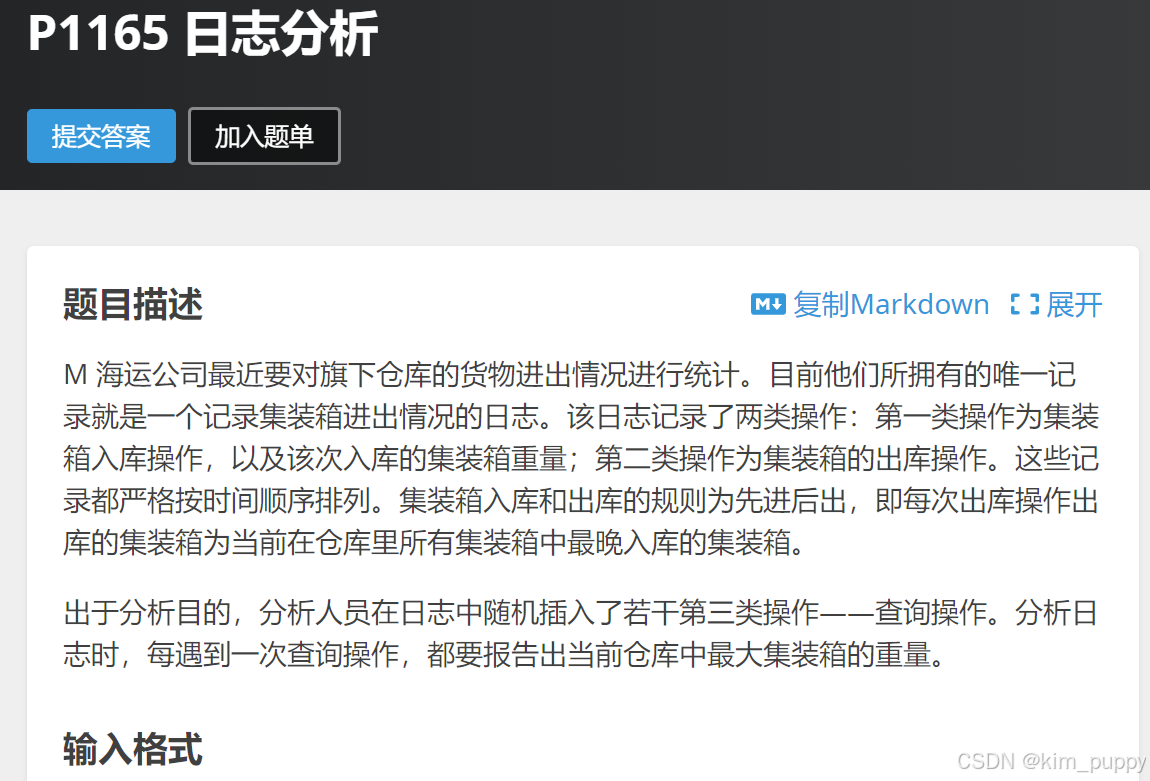

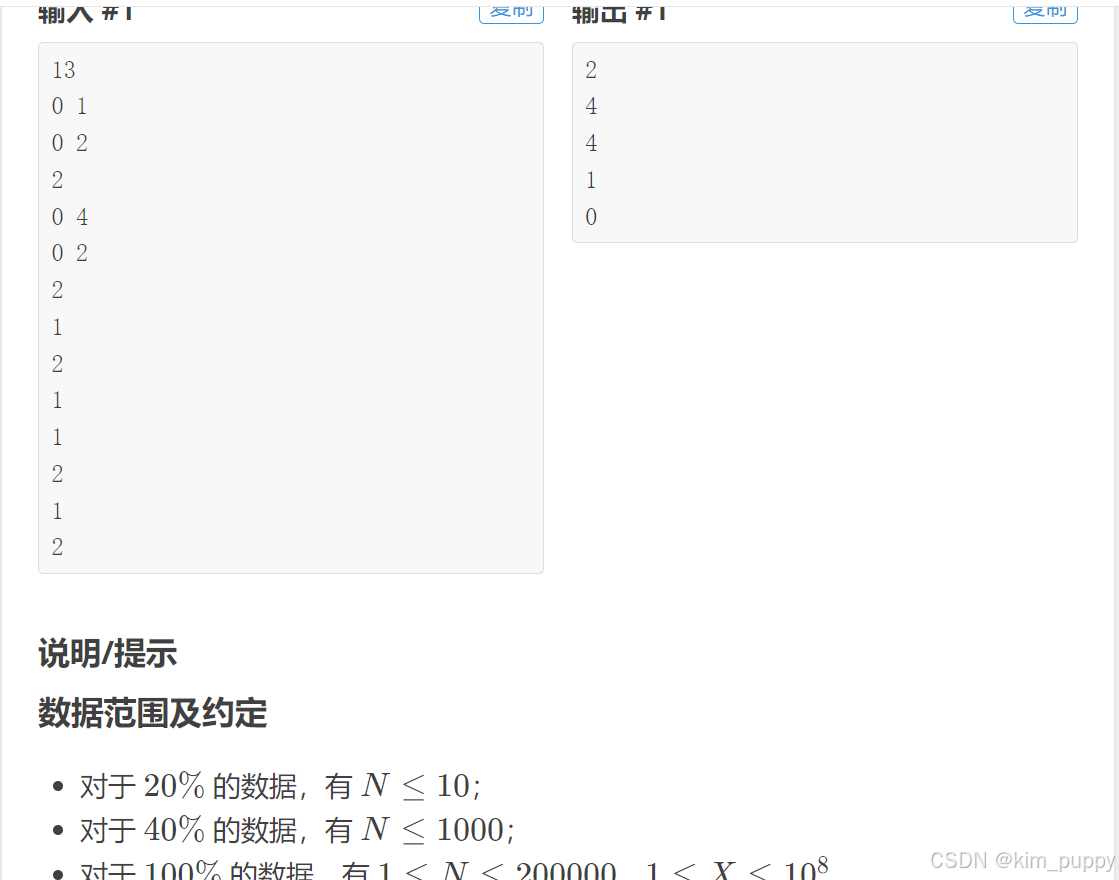
上面这道日志分析题是经典的栈的问题，要用到入栈和出栈。

在解这道题的过程中，我学习了栈。我认为要学会用栈，要明白出栈和入栈的意思。

入栈就是将一个数据放入栈顶，也可以理解为放进一个数组，数据的位置位于数组的最后面，出栈就是将栈顶的数据拿出去。通常规律就是先入栈的后出栈，后入栈的先出栈。

如果要用栈去解题，我认为主要需要两个部分：

“栈顶指针”（这里的指针不是特指指针数据类型，而是一个指向栈顶的标记，我们可以直接用一个数记录栈顶位置，这就是一个“栈顶指针”）

栈（这个简而言之就是存放数据的地方）

下面上代码，一边分析一边了解知识点

#include<stdio.h>
int data[200000];//日志数据

typedef struct
{
	int top;//栈顶标记
	int max;//最大值
}Struct;

void oringal(Struct* s)
{
	s->top = -1;//栈为空
	s->max = 0;//初始化最大值为0
}

void push(Struct* s, int weight)
{
	data[++(s->top)] = weight;//入栈
	if (weight > s->max)
	{
		s->max = weight;
	}
}

void pop(Struct* s)
{
	if (s->top >= 0)//栈不为空时
	{
		int popweight = data[s->top--];//出栈的数据
		if (popweight == s->max)
		{
			s->max = 0;
			for (int i = 0; i <= s->top; i++)//更新最大值(这里要注意是<=top,不要忽略栈顶元素)
			{
				if (data[i] > s->max)
				{
					s->max = data[i];
				}
			}
		}
	}
	
}

void Getmax(Struct* s)
{
	printf("%d",s->top == -1 ? 0 : s->max);

}

int main()
{
	Struct diary;
	oringal(&diary);//初始化

	int N = 0;
	int m = 0;
	scanf("%d", &N);
	for (int i = 0; i < N; i++)
	{
		scanf("%d", &m);
		if (m == 0)
		{
			int weight = 0;
			scanf("%d", &weight);
			push(&diary, weight);
		}
		else if (m == 1)
		{
			pop(&diary);
		}
		else if (m == 2)
		{
			Getmax(&diary);
		}

	}
	return 0;
}

在上面的解法中，我们将出栈和入栈以及输出最大的部分进行分装，让操作更加清晰。

重点：

入栈，将栈顶指针上移，并在栈顶指针指向的位置放入入栈的数据。

出栈，将栈顶指针下移，释放栈顶的数据。

判断栈是否已满或栈是否为空。

第二个栈题

与第一个大同小异，稍微扩展了一点，下面来分析

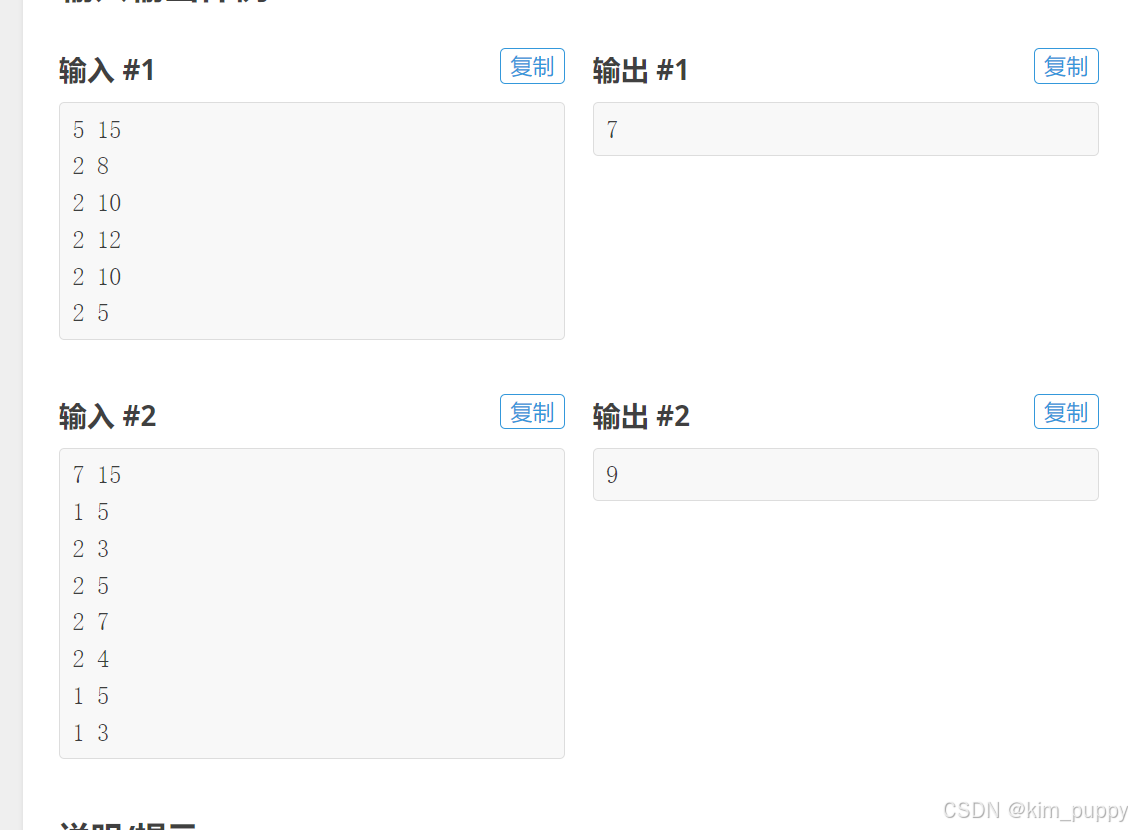
这道题与第一个题目的区别有几点：

需要同时有几个不同的栈

出栈入栈的判断条件（手指动的次数的判断条件）

一个个解决：

需要同时有几个不同的栈：这里我们可以创建一个二维数组，例如a[ ][ ]，而前半部分a[ ]可以看做是栈，这样我们就可以拥有一些不同的栈。后半部分可以看做是指向不同的位置。在题目中，后半部分是用于指向栈顶的位置。

出栈入栈的判断条件：如果要放入的数据比栈顶的数据要大，则需要入栈，即动手指按琴弦。如果放入的数据比栈顶的数据要小，则需要一直出栈，直到放入的数据小于或等于栈顶数据时，退出循环。这里需要注意的是，如果栈顶数据和放入的数据一样大的话，不需要任何操作，只有输入的数据在栈中没有，才需要入栈。

下面给出代码（代码中的注释也比较清楚）：

#include<stdio.h>
int main()
{
	int a[7][30001];
	int n = 0;
	int P = 0;//吉他弦的段数
	int s = 0;//手指动的次数
	int sum[7];//作为栈顶指针(此处栈底指针为1)
	scanf("%d%d", &n, &P);
	for (int i = 1; i <= n; i++)
	{
		int x, y;
		scanf("%d%d", &x, &y);
		
		while (sum[x] >= 1 && a[x][sum[x]]> y)//栈不为空，并且需要出栈(松手指)的情况
		{
			sum[x]--;
			s++;
		}
		//下面的步骤为判断在松完手指后是否需要按琴弦
	
		if (a[x][sum[x]] < y)//入栈(这里注意入栈要写在出栈后面，因为松完手指是否需要按琴弦有两种情况)
		{
			a[x][++sum[x]] = y;//这里主要要将整个数组等于y
			s++;
		}
	}
	printf("%d", s);

	return 0;
}

---

接水问题

比较简单，主要是解决的两个问题点是，如何让在接水的每个人每次都一起接到水，同时一个水龙头位置空出如何按顺序让下一个接水的人马上接上。

一个个解决：

如何让在接水的每个人每次都一起接到水：可以利用for循环，将每个水龙头接水的人在一次整体的while循环下都接到1。

一个水龙头位置空出如何按顺序让下一个接水的人马上接上：可以利用判断语句，判断水龙头接水的人是否已经接满，如果接满就让这个水龙头需要放出的水的值赋给这个表示水龙头的数组。

代码也放在下面：（注意t不仅表示下一个接水的同学，也表示接水的同学是否每个人都已接完）

#include<stdio.h>
int main()
{
	int n, m;
	scanf("%d%d", &n, &m);
	int s[11000];
	int t = m+1;
	int ans = 0;
	for (int i = 1; i <= n; i++)//每个学生所需的接水量(这里和下面的循环都需要注意，用1-n或m的范围会使代码更容易理解)
	{
		scanf("%d", &s[i]);
	}
	while (t <= m + n)//这里需要重点理解
	{
		for (int i = 1; i <= m; i++)
		{
			s[i]--;
			if (s[i] == 0)
			{
				s[i] = s[t];//换下一个接水
				t++;
			}
		}
		ans++;
	}
	printf("%d", ans);
	return 0;
}

---

约瑟夫问题

（一道经典题目，在提交代码的时候试了两种方法，第一种虽然简单好理解，并且自己测试时结果正确，但平台显示超时，第二种方法则没有错误，直接AC，所以将第二种方法总结一下）

题目如下：

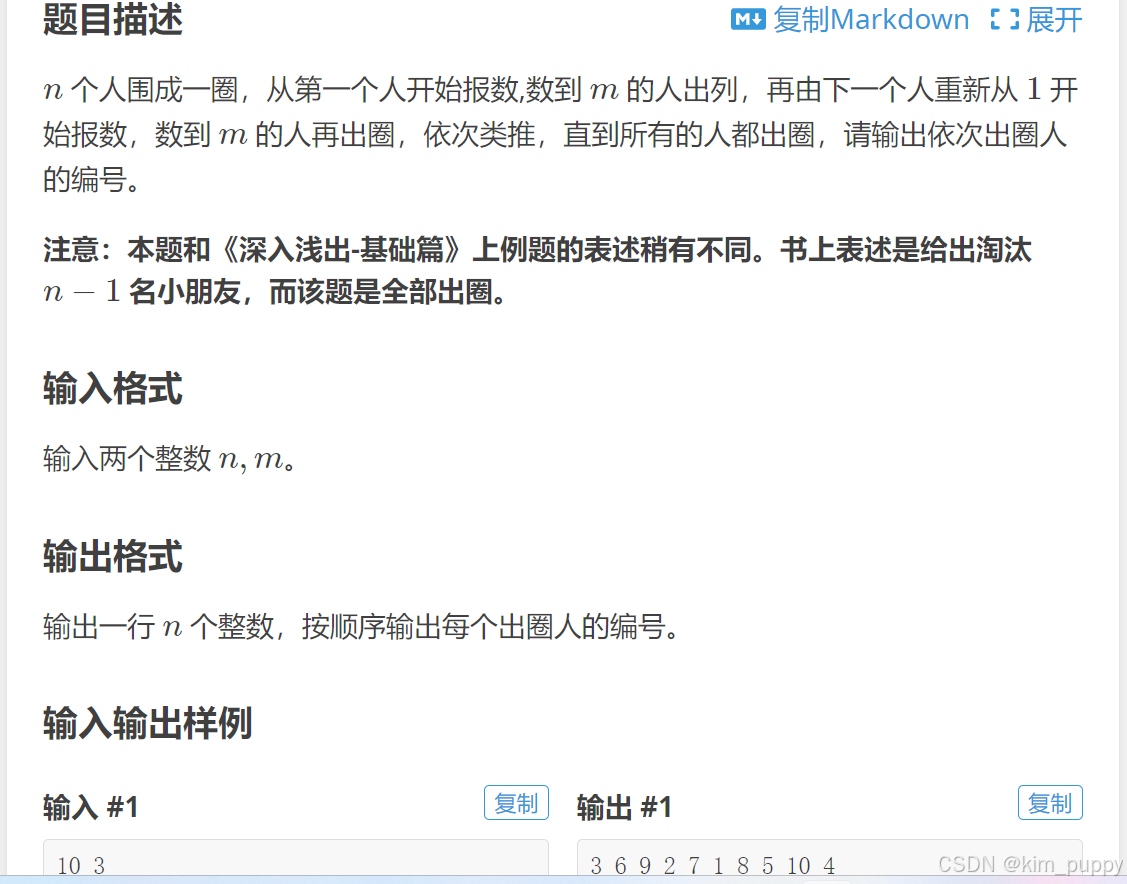
代码如下：

(正确，在使用数组解决约瑟夫问题时选择删减数组)
#include <stdio.h>
#define MAX_SIZE 100
// 约瑟夫环函数
int josephus(int n, int m)
{
    int circle[MAX_SIZE]; // 用数组表示约瑟夫环
    int i, index, count;

    // 初始化约瑟夫环
    for (i = 0; i < n; ++i)
    {
        circle[i] = i + 1;
    }

    index = 0; // 从第一个人开始(数组下标的显化)
    count = 0; // 计数器

    while (n > 1)
    {
        count++;

        if (count == m)
        {
            printf("%d ", circle[index]);

            for (i = index; i < n - 1; ++i)//将最后一个数的值给倒数第二个数即可，故n-1
            {
                circle[i] = circle[i + 1];
            }

            count = 0; // 重置计数器
            n--; // 约瑟夫环的人数减一
            index--; // 修正index以指向正确的下一个元素
        }

        index++; // 移向下一个人
        if (index == n)
        {
            index = 0;
        }
    }

    // 返回最后幸存者的编号
    return circle[0];
}

int main()
{
    int n, m;
    int survivor;
    scanf("%d", &n);
    scanf("%d", &m);
    survivor = josephus(n, m);
    printf("%d", survivor);

    return 0;
}

这个解法之所以能够AC，相较于第一个解法，这里使用的是将数组真正的删减，注意使用for循环将删减数组。

同时解这道题要注意的两个点就是所有人数都过完一轮，要重新从第一个人开始数，如何记录？每次数到要求的数，该位置就删除，并将数组缩小，并且要修正index。

所有人数都过完一轮，要重新从第一个人开始数，如何记录？——>>这里用index记录，每次当index等于n时就代表数的数已经超过总人数，此时就将index重新指向第一个人。