Matlab概率论与数理统计实践-对均值的参数估计及正态密度曲线与直方图的结合

最新推荐文章于 2024-01-17 10:30:00 发布

原创最新推荐文章于 2024-01-17 10:30:00 发布 · 1.7k 阅读

22 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #概率论 #统计学

Matlab 同时被 2 个专栏收录

12 篇文章

订阅专栏

概率论与数理统计

4 篇文章

订阅专栏

本文通过一组零件质量数据，展示了如何使用Matlab进行正态分布参数的估计和置信区间的计算，同时生成了直方图与正态密度曲线的对比图，验证了估计的准确性。

题目：
某厂生产的零件重量服从正态分布，现从该厂生产的零件中抽取9个，测得其质量（单位：g）为：
45.3 45.5 45.1 45.3 45.5 45.7 45.4 45.3 45.6
（1）求平均质量μ的置信水平为0.95的置信区间及参数估计量；
（2）作出附加有该正态密度曲线的直方图。
问题理论分析：
显然, 该置信区间为双侧置信区间, σ²未知, 则置信区间为
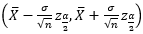
程序设计及必要注释

x=[45.3  45.5  45.1  45.3  45.5  45.7  45.4  45.3  45.6];   %输入样本
[muhat,sigmahat,muci,sigmaci]=normfit(x)    %该函数可计算正态分布中参数的估计值及置信区间
%返回的muhat即为该分布的均值的估计值,sigmahat为方差的估计值
data=normrnd(muhat,sigmahat,10000,1);    %产生一万个服从上述正态分布的随机数
histfit(data) %作图
title('题3.2 直方图和正态密度曲线');
xlabel('x')
ylabel('y')

函数说明:

[muhat,sigmahat,muci,sigmaci]=normfit(x): 根据正态分布数据 x 对参数 mu 和sigma做出估计 , 返回值 muhat 是 x 的均值的点估计 , sigmahat是标准差的点估计 , muci 是均值的置信度为 95%的置信区间 , sigmaci 是标准差的置信度为 95%的置信区间
若对置信度的要求不是默认的95%,可做如下调整:.
[muhat,sigmahat,muci,sigmaci]=normfit(x,alpha): 返回的置信区间的置信度为100(1-alpha)%.
histfit(data) :data 为向量 , 返回直方图和正态曲线 .
histfit(data, nbins)nbins: 指定 bar 的个数 , 缺省时为 data 中数据个数的平方根

结果呈现及结果分析：
muhat = 45.4111
sigmahat = 0.1833
muci = 2×1
45.2702
45.5520
sigmaci = 2×1
0.1238
0.3512

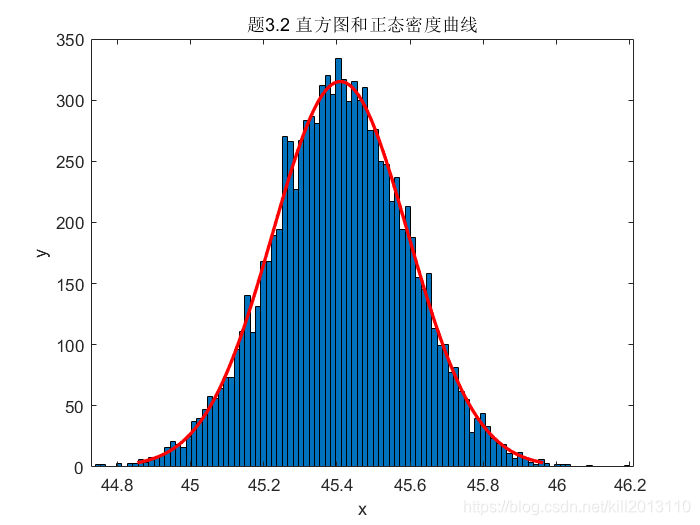
结果分析:
则所求置信区间为(45.2702,45.5520)
直方图与概率密度曲线比较吻合,若随机数的数量增多,则吻合程度将更高