蓝桥备赛（16）- 树-优快云博客

本文链接：https://blog.youkuaiyun.com/khjjjgd/article/details/146122781

一、树的概念

1.1 树的定义

1）树型结构（一对多）是⼀类重要的非线性数据结构

2 ）有⼀个特殊的结点，称为根结点，根结点没有前驱结点

3）除了根节点外，其余结点被分成 M（M > 0) 个互不相交的集合 T1 , T2.....Tm , 其中每个集合 Ti ( 1 <= i <= m) 又是一棵结构与树类似的子树。每棵子树的根节点有且只有一个前驱，可以有 0 个或者多个后继。 因此，树是递归定义的。

1.2 树的基本术语

结点的度：一个结点有几个孩子 --> 度就有多少
树的度：一棵树中，最大的结点的度称为树的度
父结点 / 双亲结点：若一个结点含有子节点，则这个结点称为其子节点的父结点
子节点 / 孩子结点 : 一个结点含有的子树的根结点称为该结点的子节点
叶子结点 / 终端结点：度为 0 的结点称为叶节点
分支结点 / 非终端结点：度不为0的结点
兄弟结点：具有相同父结点相互成为兄弟结点（亲兄弟 )
结点的层次 : 从根开始定义起，根为第一层，根的子结点为第二层，依次类推
树的高度或深度：树中结点的最大层次
路径 : 一条从树中任意结点出发，沿父结点 --> 子结点 连接，达到任意结点 的序列

树的概念与结构-优快云博客

1.3 有序树和无序树

1）有序树：结点的子树按照从左往右的顺序排列，不能更改。

2）无序树：结点的子树之间没有顺序，随意更改。

这个认知会在我们后续学习二叉树的时候用到，因为二叉树需要区分左右孩子

在算法竞赛中，遇到的基本上都是无序树，也就是说，不需要考虑孩子结点的顺序

在有序树的视角中，上面两棵树不相同；

但是在无序树的视角中，上面两棵树是相同的。

1.4 有根树和无根树

1）有根树： 树的根节点已知，是固定的。

2）无根树：树的根节点未知，谁都可以是根结点

在有根树的视角中，根结点为 : A

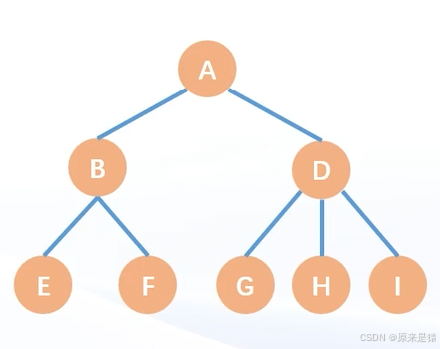
在无根树的视角中：

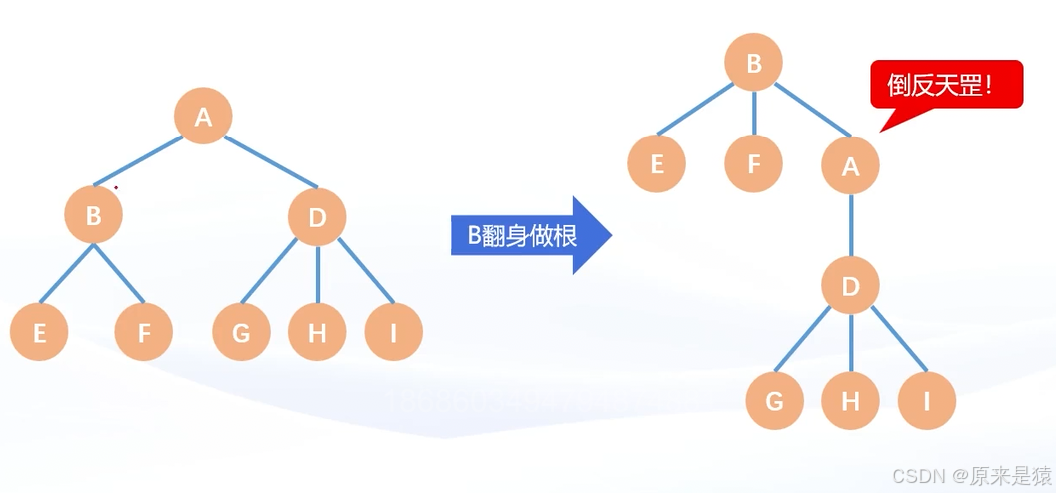
无根树会导致父子关系不明确，在存储时候需要注意。 在算法竞赛中，一般遇到的树一般都是无根树，即使有根树，也会存在父子关系未知的情况。

二、树的存储

1）树结构相对线性结构来说就比较复杂 。存储时，既要保存值域，也要保存结点与结点之间的关系。

2）实际中树有很多种存储方式：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。

2.1 孩子表示法

1）对于每一个结点，只存储所有孩子的信息。

注意：如果在无根树之中，如何知道谁是孩子？谁是父亲呢？

----> 管他三七二十一！！！直接把相连的结点都存储起来！！！都给我存！起！来！

2.2 实现方式一：用vector数组实现

在算法中，一般会给出树结构都是有编号的，以简化我们的操作

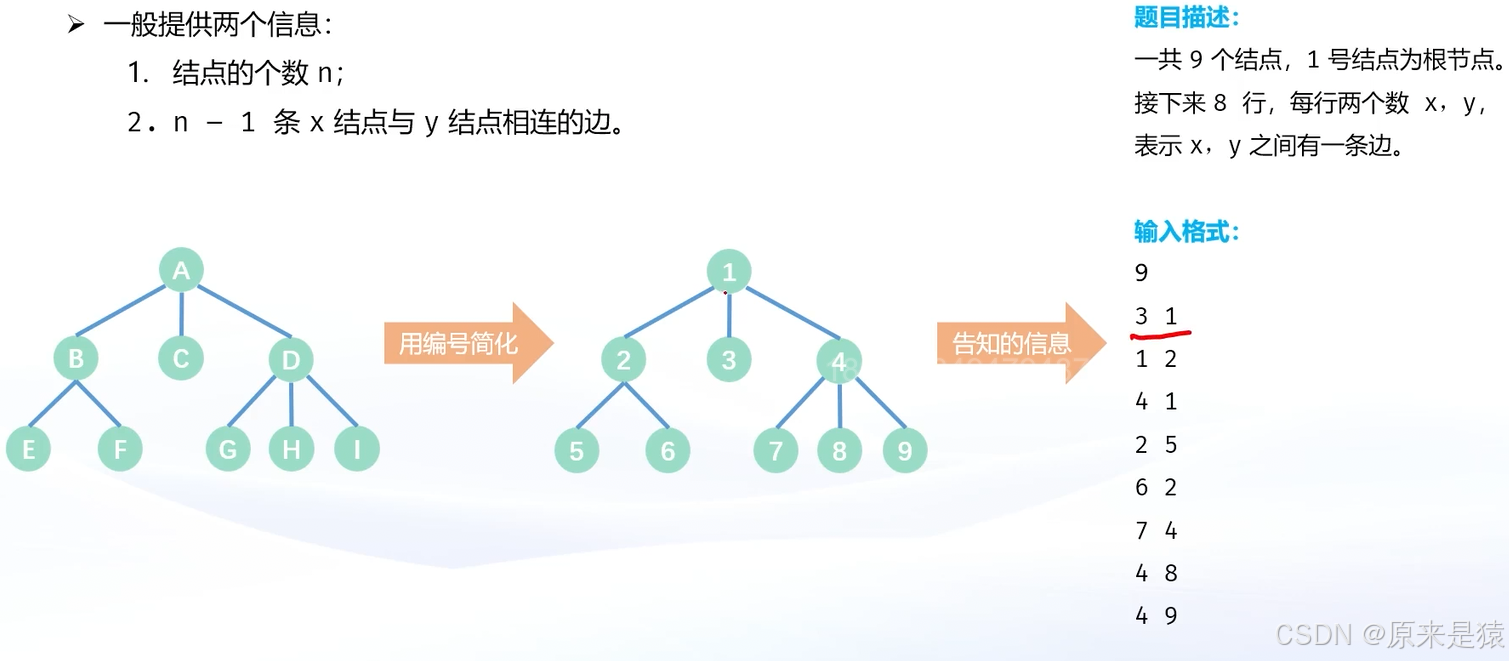
上面的题目，虽然告知了根结点是 1 ，但是其他的结点之间的关系还是未知的， 所以我们还是需要当成无序树来处理 。

1） 创建一个大小足够的 vector 数组 ：vector<int> edges[10];

2) 对于 i 的孩子，直接 edges[i] .push_back 进去即可。

#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;

const int N = 1e5 + 10;
int n;
vector<int> edges[N];

int main()
{
	cin >> n;
	for(int i = 1;i <n ;i ++)
	{
		int a,b;
		cin >> a >> b;
		edges[a].push_back(b);
		edges[b].push_back(a);  
	}
	return 0;
}

2.3 实现方式二：链式前向星

本质上就是用链表存储所有孩子，其中链表是用数组模拟实现的。

#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;

const int N = 1e5 + 10;
int h[N],e[N*2],ne[N*2],id;

int n;
//其实就是把 b 头插到 a 的链表后面 
void add(int a,int b)
{
	id++;
	e[id] = b;
	ne[id] = h[a];
	h[a] = id;
}
int main()
{
	cin >> n;
	for(int i = 1;i <n;i++)
	{
		int a,b;
		cin >> a >> b;
		add(a,b);
		add(b,a);
	}
	return 0;
}

2.4 总结

1）前者由于用到了容器 vector，实际运行起来相比较于后者更耗时，因为 vector 是动态实现的。

2）但是在如今的算法竞赛中，⼀般不会无聊到卡这种常数时间。也就是 vector 虽然慢，但不会因此而超时。

三、树的遍历

树的遍历就是不重不漏的将树中所有的点都扫描一遍

在之前学过的线性结构中，遍历就很容易，直接从前往后扫描⼀遍即可。但是在树形结构中， 如果不按照⼀定的规则遍历，就会漏掉或者重复遍历⼀些结点 。因此，在树形结构中，要按照⼀定规则去遍历。

常用的遍历方式有两种，一种是深度优先遍历，另一种是宽度优先遍历。

注意！！！

树的遍历是许多关于树的算法的知识，一定要掌握啊！！！

3.1 深度优先遍历 -DFS

1）深度优先遍历（DFS -- Depth First Search）， 是一种用于遍历或搜索树或图的算法 。

2）每次尝试向更深的结点走 --> 一条路走到黑！！！走到不能再走的时候，返回，继续走其他的路。

不撞南墙不回头！！！

因此， DFS 其实就是利用递归的形式遍历，可以用递归来实现！

3.1.1 用vector 数组存储

#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;

const int N = 1e5 + 10;
int n;
vector<int> edges[N];//存储图
bool st[N];//标记哪些点已经访问了 
//方法一：vector 实现 

void dfs(int u)
{
	cout << u << " ";
	st[u] = true;//说明当前这个点已经访问过了
	
	//访问所有的孩子 
	for(auto v:edges[u])
	{
		if(!st[v])
		{
			dfs(v);
		}
	} 
}
int main()
{
	//建树
	cin >> n;
	for(int i = 1; i< n;i++)
	{
		int a,b;
		cin >> a >> b;
		edges[a].push_back(b);
		edges[b].push_back(a);  
	 } 
	 
	 //深度优先遍历
	 dfs(1); 
	return 0;
}

3.1.2 链式向前星存储

#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;

const int N = 1e5 +10;
int id,h[N],e[N*2],ne[N*2];
int n;
bool st[N];//标记哪些点已经访问过了
 
void add(int a,int b)
{
	id++;
	e[id] = b;
	ne[id] = h[a];
	h[a] = id;
}

void dfs(int u)
{
	cout << u << " ";
	st[u] = true;
	
	for(int i = h[u];i; i = ne[i])
	{
		int v = e[i]; // 孩子
		if(!st[v])
			dfs(v); 
	}
}
int main()
{
	//建树 
	cin >> n;
	for(int i = 1;i<n ; i++)
	{
		int a,b;
		cin >> a >> b;
		add(a,b);
		add(b,a);
	}
	
	//深度优先遍历
	dfs(1); 
	return 0;
}

与使用vectoc 存储的打印结果不同，因为vector 是尾插到数的后面，但是链式前向星是头插。

时间复杂度 ：

简单估计⼀下，在 dfs 的整个过程中，会把树中所有的边扫描量两遍。边的数量为 n − 1 ， 因此时间复杂度为 O(N) 。

空间复杂度：

最差情况下，结点个数为 n 的树，⾼度也是 n ，也就是变成⼀个链表。此时递归的深度也是 n ， 此时的空间复杂度为 O(N) 。

3.2 宽度优先遍历 - BFS

宽度优先遍历( BFS --- Breadth First Search)，也叫广度优先遍历。也是⼀种用于遍或搜索树或图的算法。 所谓宽度优先。就是每次都尝试访问同⼀层的节点。如果同⼀层都访问完了，再访问下一层。

一层一层来

3.1.1 用vector 数组存储

#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;

const int N = 1e5 + 10;
bool st[N]; //标记哪一个点已经入队了
int n;
vector<int> edges[N]; 

void bfs()
{
	queue<int> q;
	q.push(1);
	st[1] = true;
	while(q.size())
	{
		int u = q.front() ;
		q.pop() ;
		cout << u << " ";
		for(auto v : edges[u])
		{
			if(!st[v])	
			{
				q.push(v);
				st[v] = true;
			}
		}	
	} 
}
int main()
{
	//建树 
	cin >> n;
	for(int i = 1 ;i< n ; i++)
	{
		int a, b;
		cin >> a >> b;
		edges[a].push_back(b);
		edges[b].push_back(a);  
	}
	
	//宽度优先遍历
	bfs(); 
	return 0;
}

3.1.2 链式向前星存储

#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;

const int N = 1e5 +10;
bool st[N];
int id,e[N*2],ne[N*2],h[N];
int n;

void add(int a,int b)
{
	id++;
	e[id] = b;
	ne[id] = h[a];
	h[a] = id;
}
void bfs()
{
	queue<int> q;
	q.push(1);
	st[1] = true;
	while(q.size() )
	{
		int u = q.front() ;
		q.pop() ;
		cout << u << " ";
		for(int i = h[u]; i ; i = ne[i])
		{
			int v = e[i];
			if(!st[v])
			{
				q.push(v);
				st[v] = true; 
			}
		}
	}
}
int main()
{
	cin >> n;
	//建树
	for(int i = 1;i<n;i++)
	{
		int a,b;
		cin >> a >> b;
		add(a,b);
		add(b,a);
	 } 
	 bfs();
	return 0;
}