LeetCode 124. Binary Tree Maximum Path Sum

题目

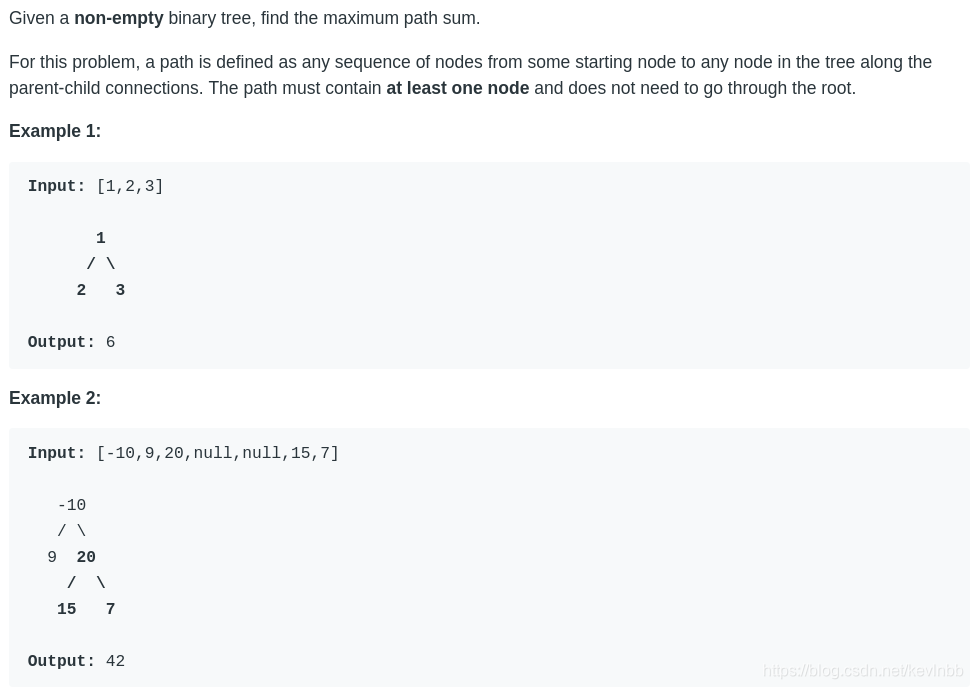
大意就是说一棵非空的二叉树，然后让你找出树中的最大路径和。所谓路径就是从树中一个结点沿着父子连接的路径构成的路径。
需要注意的是路径不能出现分叉，比如说图中样例2，如果-10改为30，那最大的路径和是从15到20到30再到9，就不能包括7了，因为题目中说了是从一个起点到一个终点，这一点也是解题的关键。

分析

leetcode给这道题的难度划分在了Hard。我觉得有道理也没道理。因为这道题看上去很难很复杂，但又没那么难理解，就像是简单dp题，如果想不明白怎么做确实很难找出最优解，但是看了答案也能很快理解。下面先分析一下这道题。

这题难就难在上来给人手足无措的感觉，因为一棵二叉树的路径有很多种，即使我们一条一条找，先不说很慢，能不能写出来找的代码都不容易。那怎么做呢？不妨从case入手。
先看第二个case，题目中说到，路径是从一个起点到一个终点，可以通过父节点，先假设树中所有的结点值都是正数，不难想象这种路径就是从左孩子到根再到右孩子，这是一种简单的贪心思想。比如case2中的黑体部分，就是从15到20再到7。类似的可以理解case1的情况。明白了这个，我们就可以把求解的代码框架搭起来：
因为我们拿到的是根节点，所以按照递归遍历的思想，不妨从根节点递归遍历到叶子然后再网上回溯，这样我们就能在回溯的时候依次得到一个结点它的左右孩子结点路径之和。
首先我们递归的找到最左边的孩子和最右边的孩子：

int findmaxsum(TreeNode* root, int& maxsum) {
        if (!root) return 0;
        int leftmax = findmaxsum(root->left, maxsum);
        int rightmax = findmaxsum(root->right, maxsum);
}

相信会写递归遍历二叉树的代码就不难理解上面的代码，其中传递的maxsum是我们需要找到的最大路径和。
按理说最大路径和传递了引用，函数就不需要返回值了，那为什么这里函数还需要返回int呢？注意，这个函数返回值并不是最大路径和，而是从孩子结点走到根的路径之和，不懂没关系，先留个印象，只要看到后面完整的部分就能明白。
写到这里，那按照递归遍历，就执行到了最左边的叶子结点，比如case2中的15，由于它是叶子，左右孩子都没有，所以左右子树路径和leftmax和rightmax都是0，所以以15为根节点的子树最大路径和就是0 + 0 + 15，接着就可以写返回值了。
注意这里就是本题的第一个注意点,我们返回的值按理说应该是左子树的值加上右子树的值加上结点的值，但是注意刚才提过的路径不能分叉，这就导致并不能返回15+0+0，比如case2中如果根是30，那从30的右孩子20返回到30的值就不能是20+15+7了，因为路径只可能从30到20再到15或7，所以正确的return应该是return max(leftmax, rightmax) + root->val，即左右孩子的较大者和这个结点的值，结点值必须要，因为路径要连续。
那如果就这么简单写完了肯定是对不起hard难度的，我们刚才考虑leftmax和rightmax的时候，只是无脑的求和，但如果leftmax值或者rightmax值是负数呢？，比方说case2中不是15和7，而是-15和-7呢？那最大路径肯定就是只有20这个结点了，所以这是第二个注意点，怎么解决左右孩子为负数的问题呢？当然可以写一个判断语句，如果是负数就不加，这里做了一个比较巧妙的处理，对leftmax的值和0进行一个max比较，如果比0小就加上0，相当于不加，这样就完美解决了负数的问题。
接着第三个注意点，最大路径和是不一定过根节点的，比如case2就没有过，所以我们最后return的结果其实不一定的最大的，那为了记录遍历过程中最大的路径和，我们传入一个引用参数maxsum，这也是之前代码中疑惑的地方，每次遍历到一个定点，就比较一下maxsum的值和当前点的路径和，这样遍历完得到的maxsum值就是最大的路径和。
说到这里，终于是把这道题的细节说完了，很多注意的点值得这道题作为一个hard。代码如下：

class Solution {
public:
    int findmaxsum(TreeNode* root, int& maxsum) {
        if (!root) return 0;
        int leftmax = max(findmaxsum(root->left, maxsum), 0);
        int rightmax = max(findmaxsum(root->right, maxsum), 0);
        // 比较的时候左右子树和加上根
        maxsum = max(maxsum, leftmax + rightmax + root->val);
        // 返回到上层的只是左右的较大者和根
        return max(leftmax, rightmax) + root->val;
    }
    int maxPathSum(TreeNode* root) {
        int maxsum = INT_MIN;
        findmaxsum(root, maxsum);
        return maxsum;
    }
};