常用的排序02（归并排序、快速排序）

1、归并排序

排序思路：把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。

举例：

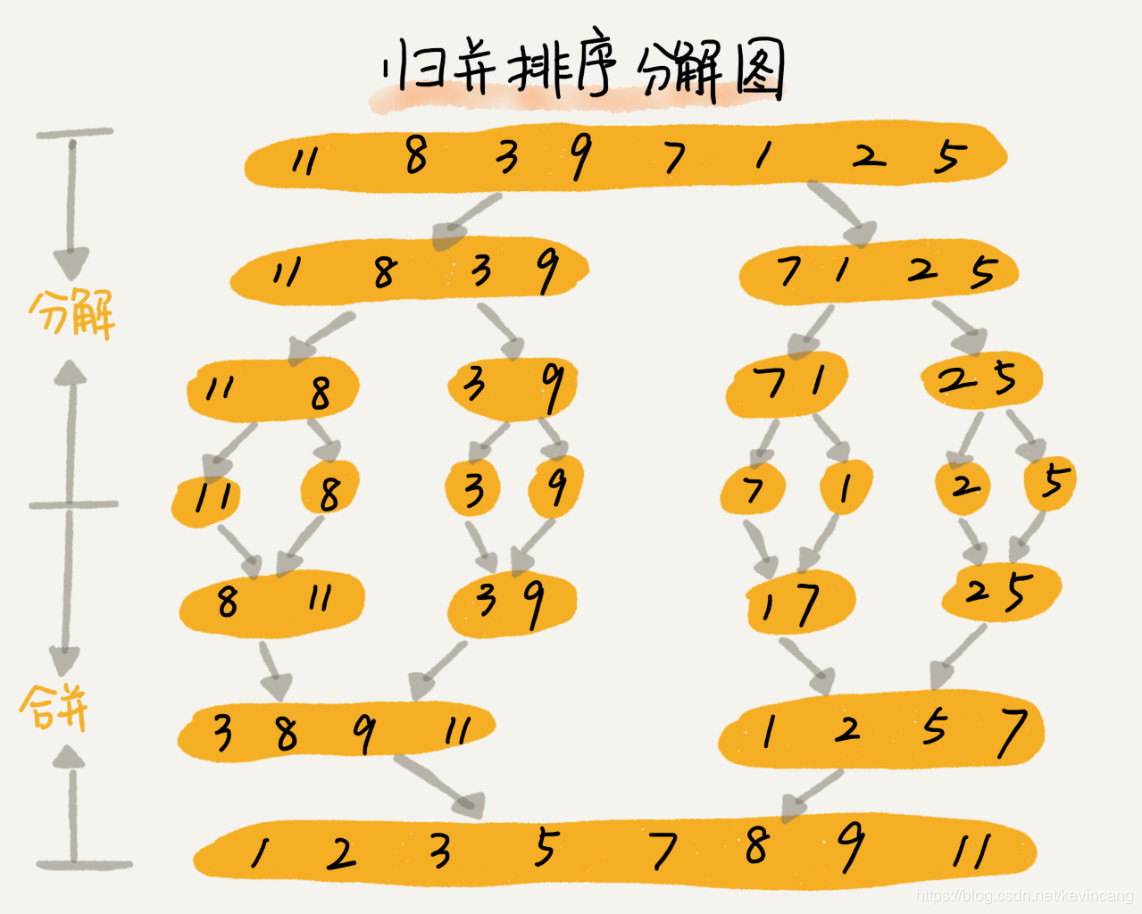
实现代码：

public class MergeSort{

    public static void sort(int[] arr) {
        int len = arr.length;
         //使用递归实现
        sort(arr, 0, len - 1);
    }

    /**
     * 递归终止条件
     * if p >= r  then return
     * 取p到r之间的中间位置q
     * q = (p+r) / 2
     * 分治递归
     * merge_sort_c(A, p, q)
     * merge_sort_c(A, q+1, r)
     * 将A[p...q]和A[q+1...r]合并为A[p...r]
     * merge(A[p...r], A[p...q], A[q+1...r])}
     *
     * @param arr
     * @param p
     * @param r
     */
    public static void sort(int[] arr, int p, int r) {
        if (p >= r) {
            return;
        }
        int q = (p + r) / 2;
        sort(arr, p, q);
        sort(arr, q + 1, r);
        int[] tempArr = new int[r - p + 1];
        int k = 0;
        int i = p;
        int j = q + 1;
        while (i <= q && j <= r) {
            //= 一定要加，稳定排序
            if (arr[i] <= arr[j]) {
                tempArr[k++] = arr[i++];
            } else {
                tempArr[k++] = arr[j++];
            }
        }
        if (i <= q) {
            for (; i <= q; i++) {
                tempArr[k++] = arr[i];
            }
        } else if (j <= r) {
            for (; j <= r; j++) {
                tempArr[k++] = arr[j];
            }
        }
        for (int l = p; l <= r; l++) {
            arr[l] = tempArr[l - p];
        }
    }

    public static void main(String[] args) {
        int[] arr = {3, 1, 2, 4, 5, 6, 8, 7};
        sort(arr);
        Console.log(Arrays.toString(arr));
    }
}

复杂度：

​1、空间复杂度为 O(n)，非原地排序算法。
2、时间复杂度为 O(nlogn)。最好 最坏都为 O(nlogn)
3、稳定的排序算法。

2、快速排序

排序思路：如果要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的。递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据，直到区间缩小为 1，就说明所有的数据都有序了。

举例：

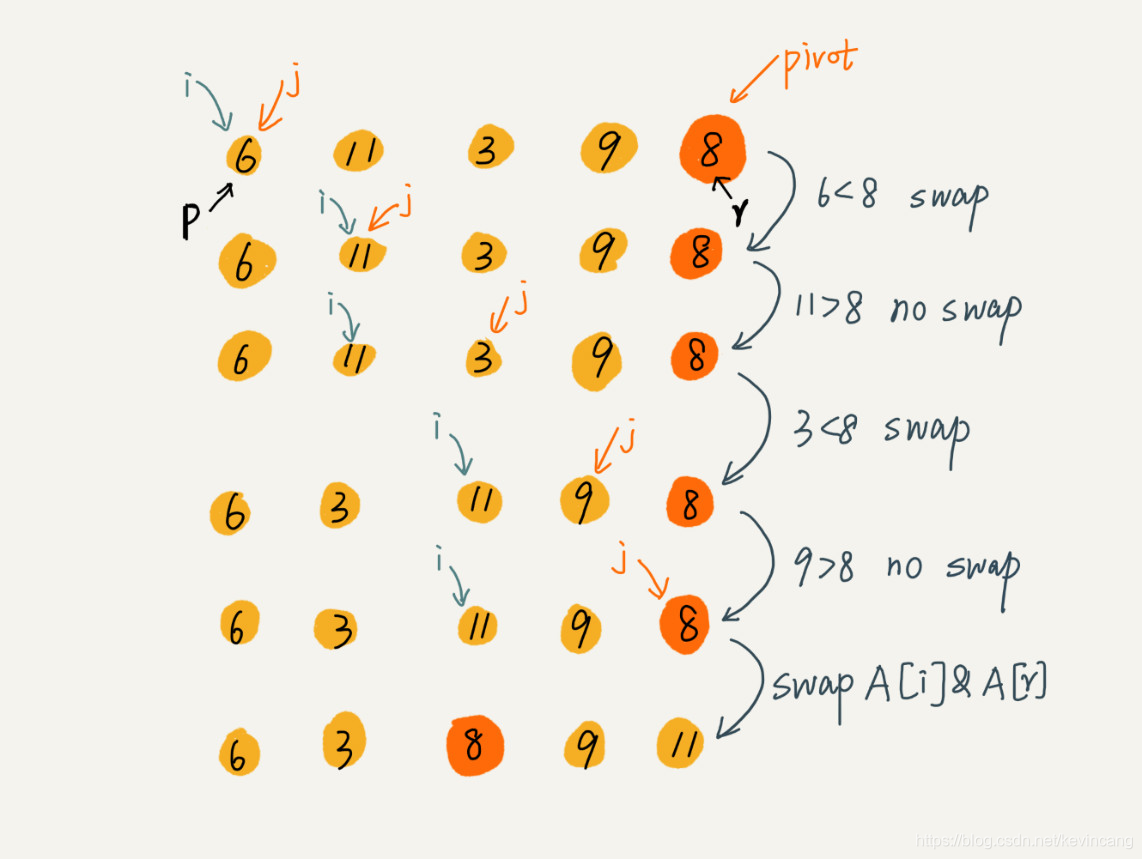
实现代码：

public class QuickSort{

    public static void sort(int[] arr) {
        int len = arr.length;
        quickSort(arr, 0, len - 1);
    }

    public static void quickSort(int[] arr, int p, int r) {
        if (p >= r) {
            return;
        }
        int val = arr[r];
        int i = p;
        for (int j = p; j <= r; j++) {
            if (arr[j] < val) {
                int temp = arr[j];
                arr[j] = arr[i];
                arr[i] = temp;
                i++;
            }
        }
        arr[r] = arr[i];
        arr[i] = val;
        int q = i;
        quickSort(arr, p, q - 1);
        quickSort(arr, q + 1, r);
    }

    public static void main(String[] args) {
        int[] arr = {3, 1, 2, 4, 5, 6, 8, 7};
        sort(arr);
        Console.log(Arrays.toString(arr));
    }
}

复杂度：

1、空间复杂度为 O(1)，原地排序算法。
2、时间复杂度为 O(nlogn)。分割点均分数据，最好 O(nlogn) 最坏为 O(n^2)
3、非稳定的排序算法。

3、两者对比

两种排序都是利用分治的思想，两者的区别：归并排序的处理过程是由下到上的，先处理子问题，然后再合并。而快排正好相反，它的处理过程是由上到下的，先分区，然后再处理子问题。归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法，但是它是非原地排序算法。快速排序通过设计巧妙的原地分区函数，可以实现原地排序，解决了归并排序占用太多内存的问题。