无监督学习之稀疏编码，自编码

---

前言

---

一、稀疏编码

1.基本概念

稀疏编码这一概念来源于神经生物学，例如看到的每幅画都是上亿像素的，但在初级视觉皮层中。每个神经元只对特定的刺激信号做出响应（例如特殊条纹，特定方向的边缘），每幅画像经过大脑处置之后只用较小的代价取重建和储存，仅存入重要的信息。
以此类比，外界的信息在经过编码后仅有一部分神经元被激活，即外界信息在神经系统的表示上有稀疏性。
稀疏编码的目的：在大量的数据集中，选取很小部分作为元素来重建新的数据。
编码的概念：（线性）编码指将输入样本$X\in R^D$，表示为一组基向量$A=[{\alpha }_1,...{\alpha }_M]$的线性组合。
$$x={\Sigma }_{m=1}^M{z}_m{\alpha }_m$$
X 表示D维空间的样本，例如一幅图片

A为标准化 的基础矩阵，表示构成组成元素的基本原子，可称为字典，在图像中可表示为构成图像的基本边，角。

• A为基向量（字典）。Z为编码（基向量的系数），AZ表示经过编码后的x，表示外界环境经过编码后只有一小部分神经元被激活，则外界刺激在系统的表示中具有很高的稀疏性。

• 注：稀疏性的定义：非零元素的比例。若向量z中仅有几个非零元素则说明该向量是稀疏的。

  维度角度：D维空间中的样本x 找到其在P维空间的表示，为了稀疏编码需要找到一组“过完备的基向量，因为过完备的基向量下往往存在冗余，因此会出现很多有效的编码。（根据线代知识，P>D ，则说明这个稀疏矩阵有很多解）
  对这些编码加一个稀疏性限制，将减少解空间大小，得到唯一的稀疏性编码。

2. 模型算法

给定一组N个输入向量。目标函数为
$\rho$表示衡量稀疏性函数-z越稀疏，$\rho (z)$越小，$\eta$超参数，用来控制稀疏性强度。
其中，衡量稀疏性函数有多种形式：

二、自编码

1. 概念

上面两组数据如果让你记忆，哪一行数据会更容易记住呢？咋一看，可能会觉得肯定是第一行，但仔细分析后发现第二组数据长，但存在一定规律，偶数项的后一项是除2得到的数，奇数项的后一项是三倍加一。这个过程就涉及到记忆、感知、和模式匹配的关系。
和这样的记忆模式类似，一个自编码器接收输入，将其转换成高效的内部表示，然后再输出输入数据的类似物。自编码器通常包括两部分：encoder（也称为识别网络）将输入转换成内部表示，decoder（也称为生成网络）将内部表示转换成输出。
自编码器通过简单地学习将输入复制到输出来工作。这一任务就是输入训练数据， 再输出训练数据的任务，输入数据进行一高效表示，其维度一般远小于输入数据。

自编码用途

1. 限制内部表示的尺寸，从而实现降维
2. 作为强大的特征检测器（feature detectors），应用于深度神经网络的预训练
3. 随机生成与训练数据类似的数据，这被称作生成模型。例如用人脸图片训练一个自编码器，它可以生成新的图片。
4. 对训练数据增加噪声并训练自编码器使其能恢复原有。这些限制条件防止自编码器机械地将输入复制到输出，并强制它学习数据的高效表示
5. 若让编码的输出只能取K个不同的值，则自编码器转化为K聚类

结构

学习目标：最小化重构错误

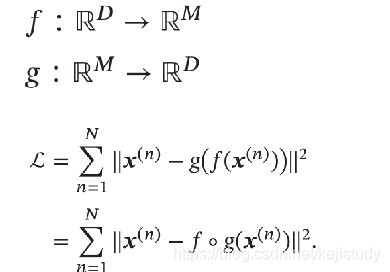
• 特征空间的维度小于原始空间的维度，相当于降维/特征抽取；
• 特征空间的维度大于原始空间的维度，则一定可以找到一组或多组解将$f。g$变为单位函数，从而使重构错误为0，这样的解没有多大意义，但如果加上编码的稀疏性等约束则可以解决一些有意义的问题。
• 
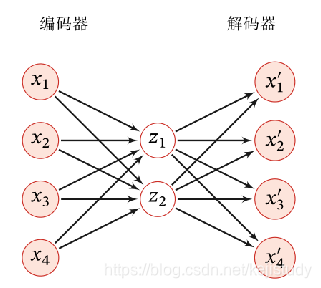
  -自编码器的结构和多层感知机类似，除了输入神经元和输出神经元的个数相等。

去噪编码器

一种强制自编码器学习有用特征的方式是输入增加噪声，通过训练之后得到无噪声的输出。这防止了自编码器简单的将输入复制到输出，从而提取出数据中有用的模式。
提升编码系统的鲁棒性。高维数据一般具有信息冗余，比如从一张部分损坏的图像去联想其完整的数据。同比，我们希望从部分损坏的数据中得到有效数据然后恢复完整的原始信息。
噪声可以是添加到输入的纯高斯噪声，也可以是随机丢弃输入层的某个特征，类似于dropout。