【Ybtoj 第22章例4】选课方案【树形DP】

---

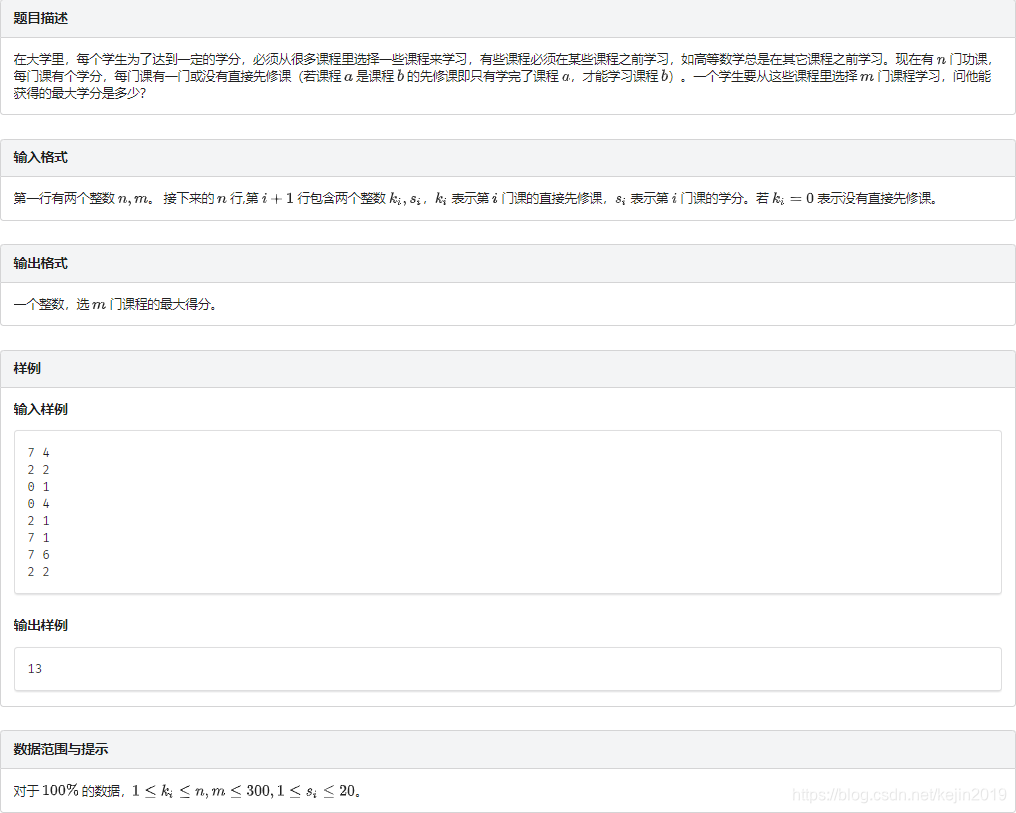
解题思路

这道题是经典的树上背包问题，把每个节点看做物品，则子节点是依赖于父节点的。

设$f[dep][j]$表示处理到节点$dep$，选了$j$节课可以得到的最大学分。设y为$dep$的子节点，$s[dep]$表示选课程dep能够获得的学分，得：
$f[dep][j]=max(f[dep][j-1],f[dep][j-k-1]+f[y][j])+s[dep];$

首先建树存图，这里的处理有一个小技巧，就是如果有多个根结点，那么不容易进行DFS，所以我们构造出一个最大的爸爸0结点，刚好，输入时也是用0来代替的，这样所有树的爸爸都是0的儿子，把$m++$，这样只用在最后输出时调用$[m+1]$。

方程也变成$f[dep][j]=max(f[dep][j],f[dep][j-k]+f[y][j])+s[dep];$
注意一开始所有 $f[dep][1]=s[dep]$

---

代码

#include<iostream>
#include<cstdio>
#include<iomanip>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#define ll long long
using namespace std;

int f[350][350],r[350],n,u,w,m,head[350];

struct c{
	int x,next;
}a[350];

void add(int x,int y)
{
	a[++w].x=y;
	a[w].next=head[x];
	head[x]=w;
}

void dfs(int dep){
	for(int i=head[dep];i;i=a[i].next)
		dfs(a[i].x);
	for(int i=head[dep];i;i=a[i].next)
	{
		int y=a[i].x;
		for(int j=m;j>0;j--)
		{
			for(int k=0;k<j;k++)
				f[dep][j]=max(f[dep][j],f[dep][j-k]+f[y][k]);
		}
	}

}

int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		scanf("%d%d",&u,&f[i][1]);
		add(u,i);
	}
	m++;
	dfs(0);
	printf("%d",f[0][m]);
}
/*
7 4
2 2
0 1
0 4
2 1
7 1
7 6
2 2*/