N-Queens

Problem

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.

Example 1:

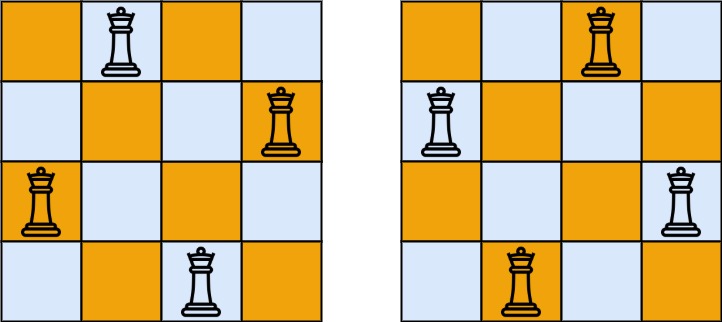
Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above

Example 2:

Input: n = 1
Output: [["Q"]]

Intuition

The N-Queens problem is a classic problem in which the task is to place N queens on an N x N chessboard in such a way that no two queens attack each other. The problem can be solved using backtracking. The idea is to explore all possible configurations of queen placements on the chessboard and backtrack whenever a conflict is encountered.

Approach

Backtracking Function (backtrack):

The backtracking function takes a parameter r representing the current row.
In the base case, if r is equal to n, it means queens have been successfully placed in all rows, and a valid solution is found. In this case, create a copy of the current board configuration and add it to the result (res).
Otherwise, iterate over all columns (c) in the current row and check if placing a queen at position (r, c) is valid. The validity is checked by ensuring that the column (c), the positive diagonal (r + c), and the negative diagonal (r - c) are all available. If valid, mark the positions as occupied and proceed to the next row (r + 1).
After the recursive call, backtrack by removing the queen from the current position.
Initialization:

Initialize sets (col, posdiag, negdiag) to keep track of occupied columns, positive diagonals, and negative diagonals.
Initialize an empty list res to store the final result.
Create a 2D board (board) filled with dots ('.') to represent the chessboard.
Backtracking Invocation:

Invoke the backtrack function with the initial row index (r = 0).
Return Result:

Return the final result (res), which contains all distinct solutions to the N-Queens puzzle.

Complexity

• Time complexity:

The time complexity is O(N!), where N is the number of queens to be placed. The backtracking algorithm explores all possible configurations, and there are N choices for each row.

• Space complexity:

The space complexity is O(N^2) due to the space required for the chessboard (board) and the sets (col, posdiag, negdiag). The recursion stack also contributes to the space complexity.

Code

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        col = set()
        posdiag = set()
        negdiag = set()

        res = []
        board = [['.'] * n for i in range(n)]

        def backtrack(r):
            if r == n:
                copy = [''.join(row) for row in board]
                res.append(copy)
                return
            
            for c in range(n):
                if c in col or (r + c) in posdiag or (r - c) in negdiag:
                    continue
                
                col.add(c)
                posdiag.add(r + c)
                negdiag.add(r - c)
                board[r][c] = 'Q'

                backtrack(r + 1)
                
                col.remove(c)
                posdiag.remove(r + c)
                negdiag.remove(r - c)
                board[r][c] = '.'
        
        backtrack(0)
        return res