遗传算法是一种模拟自然选择的优化算法。
生物学中的遗传过程:
染色体——一些基因突变——部分交叉交换——生成个体——每个个体有不同的适应性,用数字量化(适应性越强的个体活到下一代概率越大)——活到下一代的个体开始新的一轮遗传
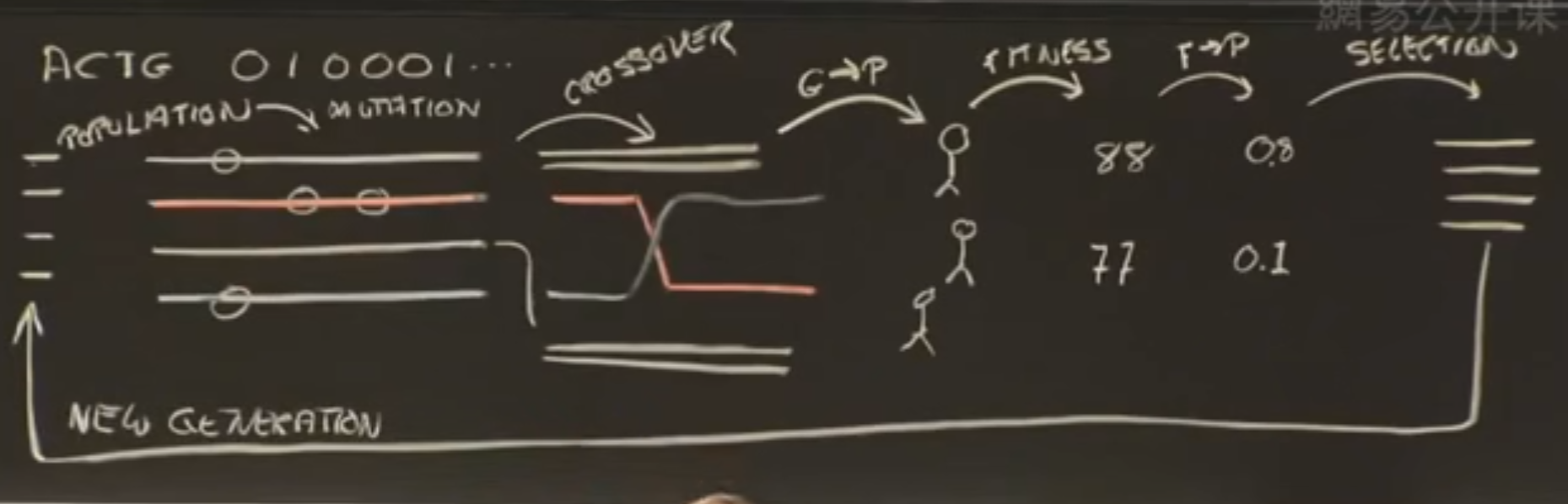
突变:就是在爬山
交叉互换:将多个个体的优点集中在一个个体身上
一、适应性
如何基于适应性 计算活到下一代的概率?
1、每个个体活到下一代的概率加起来应该是=1的。
2、选出第i个个体的概率PiP_iPi正比于个体的适应性fif_ifi。
Pi=fi∑ifi
P_i=\frac{f_i}{\sum\limits_{i}f_i}
Pi=i∑fifi
例子:用遗传算法寻找空间中的最佳值
空间:很多等高线,很多山

适应性是xy的函数,可以这样表示:
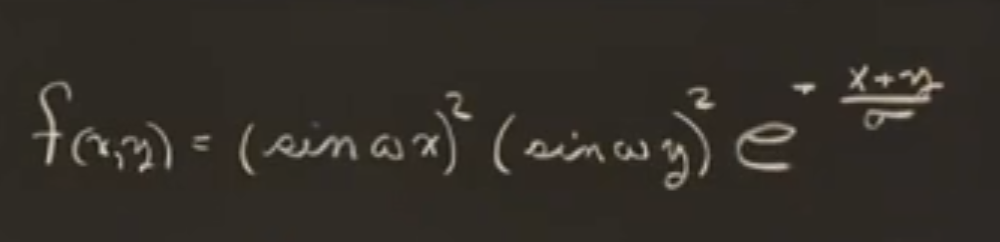
这里的α\alphaα和β\betaβ是为了让演示图象更好看。
计算时,几个x-y对会发生突变(比如x从0.3变成0.2),也会进行交叉互换。
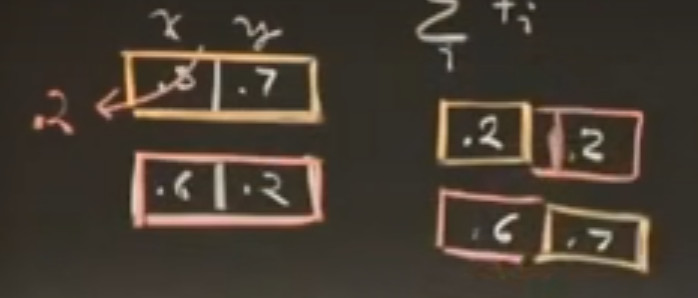
不加交叉互换(本质上还是爬山机制):卡在了局部极大值

加了交叉互换:

或许能到,但是不确定。因为无法控制随机数。
改进:提高步长。也不是很明显。

如何将适应性更好地转化为生存概率?
二、一个更好的思路:排序空间、模拟退火
排序空间 Rank Space
关心适应性最强的排序,而不是具体适应性是多少。
适应性最强的候选者将有最大概率活到下一代。(类似于赋分制)
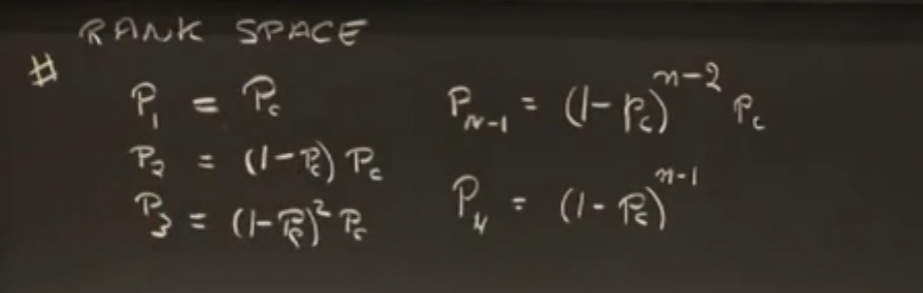
选第一个的概率 = pcp_cpc
选第二个的概率=没选第一个,且选了第二个 =(1−pc)×pc(1-p_c)\times p_c(1−pc)×pc
后面依次类推。
效果:
小步长依然会困在局部最大值

但是调大步长就会很快到全局最大值

再将步长调小,就可以锁定在全局最大值。
大步长开始,逐渐缩小到小步长——模拟退火 simulated annealing。这样就能爬上全局最优值。
但是在更复杂一点的空间(壕沟问题)中,会倾向于卡在局部最优解。

三、考虑多样性
多样性:这一代和上一代的差异有多大
优先考虑适应性最强、多样性也最强的个体。如果没有同时满足的,就可以画等优线(图中的弧线)。
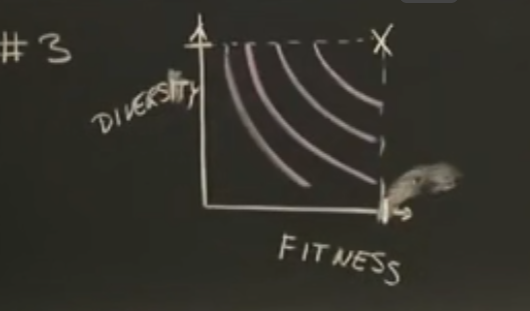
这个例子在实际运用时,是先选适应性最强的,然后剩下的候选者按照多样性进行排序。

就会扩散开,然后将多样性关掉,还是用适应性,就能锁在全局最优。

壕沟问题:很快就能到右上角,关掉多样性,再次锁在全局最优。


一些实例
可以用在什么上面?
1、做计划
两个计划各有步骤,可以交叉互换其中的步骤。

2、将基因突变和交叉互换写成规则:
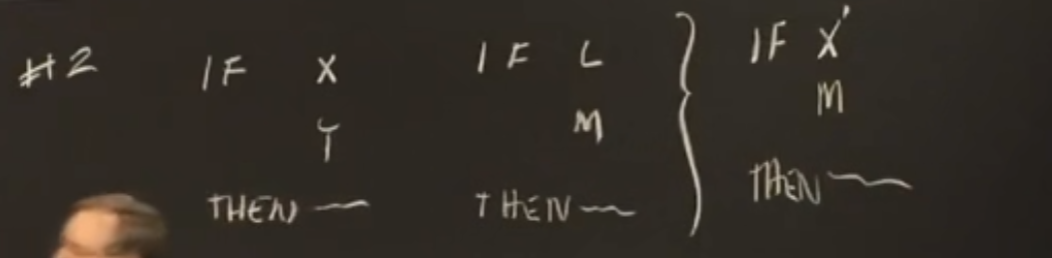
X‘就是稍微突变后的X。
那么遗传算法就是我们最想要的吗?
一个算法的结果很有趣,贡献在于空间的丰富性和编程者的聪明才智,而不在于遗传算法本身有多好。





















 538
538

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








