【概率论与数理统计】猴博士笔记 p33-35 超几何分布、正态分布、二项分布

本文链接：https://blog.youkuaiyun.com/karshey/article/details/124213108

这篇博客详细讲解了超几何分布H的应用，通过例题展示了如何计算概率、期望和方差。接着，博主探讨了一维正态分布的性质，包括概率密度函数的计算、性质及标准正态分布。此外，还介绍了正态分布的线性组合，以及如何通过标准化将任意正态分布转化为标准正态分布。最后，涉及到了二项分布，解释了中心极限定理在大样本下的应用，并给出了几个计算概率的例子。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

超几何分布H

在这里插入图片描述
例1：
设随机变量X~H(5,3,2)，求P{X=1}、EX、DX.
解：
题意是：共有5个球，其中3个目标球，共取2次，取到1个目标球的概率。
$P\{X=1\}=\frac{3}{5} \\EX=\frac{6}{5} \\DX=\frac{9}{25}$

正态分布N

一维正态分布

在这里插入图片描述
总体考点公式如下：

对第1点：
$P在\{X在a到b之间\}=\Phi(\frac{b-\mu}{\sigma})-\Phi(\frac{a-\mu}{\sigma}) \\\Phi(+∞)=1，\Phi(-∞)=0，\Phi(0)=0.5，\Phi(a)=1-\Phi(-a)$
例1：

解：套公式。（其实这两个概率加起来为1）

例2：
在这里插入图片描述
解：0.5，0.5。

例3：

解：0.3.

例4：
在这里插入图片描述

解：

上题那样的其实不会考，但是会考：（注意考点二）
$\Phi(a)>\Phi(b)=>a>b$
在这里插入图片描述

考点3：
$\\标准正态分布 => \mu=0,\sigma=1$

代入正态分布的函数得考点4：

考点5：
$若X\sim N(\mu_1,\sigma_1^{2}),Y\sim N(\mu_2,\sigma_2^{2}),且X与Y相互独立，则\\aX+bY+c \sim N(a\mu_1+b\mu_2+c,a^{2}\sigma_1^{2}+b^{2}\sigma_2^{2})$

例6：
在这里插入图片描述

解：套考点公式和正态分布公式即可。
在这里插入图片描述

考点6：
$\sim N(a\mu+c,a^{2}\sigma^{2})$
例7：

解：N(2,9).

结合考点5、6：考点5中令b=0，得到的式子就是考点6
在这里插入图片描述
考点7：标准化。(可以由考点6推出)
$\sim N(\alpha,\beta) => \frac{X-\alpha}{\sqrt\beta} \sim N(0,1)$
例8：

解：
$\frac{X-2}{3}$

考点8：
在这里插入图片描述
例9：

$\theta \\\frac{1}{2}$

例10：
在这里插入图片描述
解：和上题一样。考试的时候不会直接告诉我们期望和方差是多少，而是放在正态分布公式里告诉我们。

例10-1：
在这里插入图片描述
解：和上两题一样。
实际上，考试会考的更复杂：把正态分布的公式拆开。

记下这个公式，进行一些玄学的猜答案：

例11：

解：
对蓝色的式子：指数多出来的常数单独乘出来即可（倒数第3个等号）
在这里插入图片描述
对红色的式子：

$其实就是看积分里是xe还是x^{2}e \\如果是xe，那就是A\mu \\如果是x^{2}e，那就是A(\mu^{2}+\sigma^{2}) \\A是式子中多出来的系数，若没有，A就是1$
一个是E(X)，一个是E(X²).

二维正态分布（考得不多）

在这里插入图片描述
例12：一道概念题。

解：
A：X。不符合考点2.
B：√。符合考点2.
C：X。还要X，Y相互独立才行。见一维正态分布的考点5.
D：X。X和Y符合二维正态分布时，不相关与独立等价（考点1的④），而这里题干只是符合正态分布，没有说是二维正态分布。

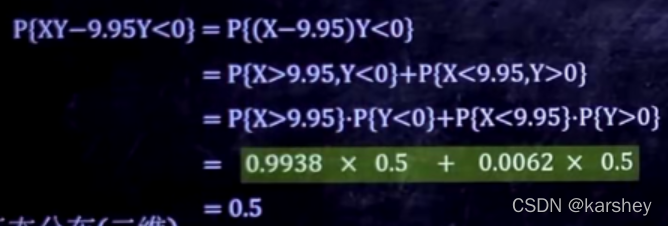
例13：
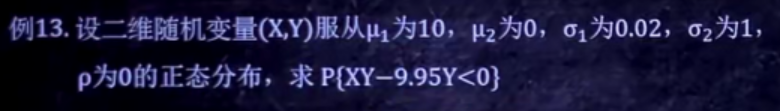
在这里插入图片描述
解：
一般二维正态分布要求概率，ρ会等于0.
步骤是要把X、Y拆开求——把XY怎样的概率变为X怎样乘以Y怎样。
第2到第3个等号由X、Y相互独立推出。
然后就是代入求值即可。

二项分布B

在这里插入图片描述
ps:③是中心极限定理。
例1：

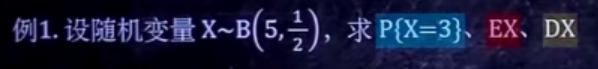
解：
套公式：
$P\{X=3\}=\frac{5}{16} \\EX=\frac{5}{2} \\DX=\frac{5}{4}$
例2：

解：
题意其实是：
$\sim B (100,0.1),求P\{X <= 10\}$
这里100太大了，很难算。根据考点③，我们知道它其实服从正态分布：
$\sim N(10,9),求P\{X <= 10\}$
因此：
在这里插入图片描述
例3：

解：D。其实就是代入正态分布的公式：
$\frac{X-\alpha}{\sqrt\beta}$