【数据结构】零基础树状数组笔记

参考和引用

树状数组学习笔记
树状数组 数据结构详解与模板(可能是最详细的了)
树状数组（简单介绍）
树状数组小结
AcWing 241. 楼兰图腾 的题解
树状数组求逆序对模板（转）
树状数组逆序对

树状数组的作用

树状数组，也叫做二叉索引树，或Fenwick树。
可以高效实现两个操作：

1. 数组前缀和的查询
2. 单点更新——某个点增加/减少x（是改变多少）

时间复杂度
朴素算法
单点修改：O(1)
区间查询：O(n)

使用树状数组
单点修改：O(logn)
区间查询：O(logn)

容易求前缀和，也容易求区间和，如：

已知nums=[1,2,3,4,5,6,7].
区间[3,7]=区间[1,7]-区间[1,2].

这里就有了一个问题：如果我要“单点更新”，那么单点更新了，前缀和也要更新。频繁地更新单点和前缀和会使其不高效。
树状数组就是高效实现前缀和和单点更新的数据结构。

什么是树状数组

长成这样：

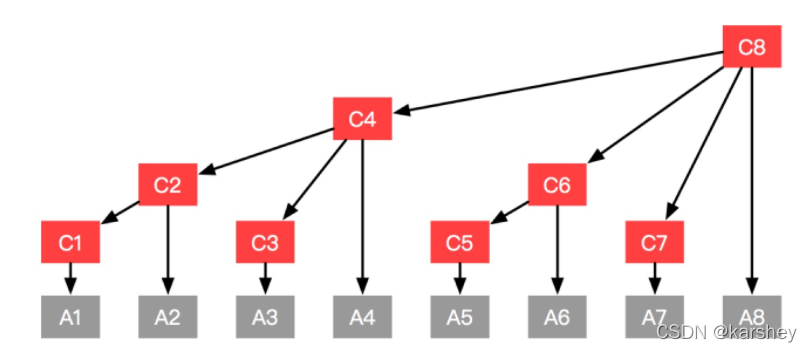
有8个数：A1-A8
有一个树状数组C
C1管A1
C2管A2，C1
C3管A3
C4管C3，A4
以此类推。

因此，我们若是改了A1，只需要更新C1，C2，C4，C8即可。

如何定义树状数组

注意，树状数组是下标从1开始的数组。

我们先记住：
C数组是对原始数组A的预处理数组。
记号i表示C的索引下标，j表示A的索引下标。

此图可以这样理解（我瞎编的助于理解的方法）：

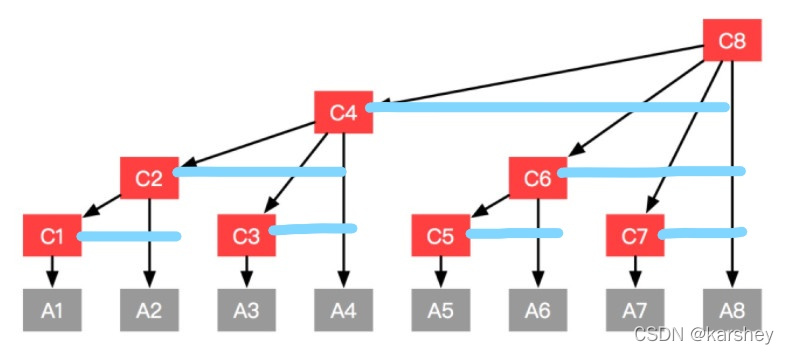
A1上没有横线，所以C1只有1格
A2上有C1的横线，所以C2比C1高1格，共2格
A3上没有横线（A1的横线已经被用掉了），所以C3只有1格
A4上有C3和C2的横线，所以C4有3格
...
A8上有C7，C6，C4的横线，所以C8有4格
横线只能用一次。

正确的理解（与二进制有关）：

即：

树状数组C和原数组A的关系

伟大的计算机科学家注意到上表中标注了“数组 C 中的元素来自数组 A 的元素个数”，它们的规律如下：将数组 C 的索引 i表示成二进制，从右向左数，遇到 1 则停止，数出 0 的个数记为 k，则计算 2^k 就是“数组 C 中的元素来自数组 A 的个数”，并且可以具体得到来自数组 A 的表示，即从当前索引 i开始，从右向前数出 2^k 个数组 A 中的元素的和，即组成了 C[i]。

计算 2^k 就是“数组 C 中的元素来自数组 A 的个数和组成C[i]的例子：

C[8]往前数8个，即从A[1]到A[8]
C[4]往前数4个，即从A[1]到A[4]
诸如此类。

如何计算2^k——lowbit

lowbit(i)=i&(-i);

一个直观的解释：
负数是一个数取反+1.
加的1的位置就是i&(-i)后从右向左的第一个1.

单点更新

找到祖先的公式：

parent(i)=i+lowbit(i)

假如要改A[3]，从图中我们可以直观地得知要更新C[3],C[4],C[8].

因为要改A[3]，所以从3开始，改完C[3]后开始计算要改的下一个C的下标：
3:3+lowbit(3)=4;
4:4+lowbit(4)=8;
....

所以C[3],C[4],C[8]是要更新的。

也可以看这个图：

前缀和查询

还是上面的图，如何求前缀和(6)?
由图可知，C[4]+C[6]即可。C[4]=A[1]+…+A[4],C[6]=A[5]+A[6].

如何求前缀和(5)?
C[4]+C[5]即可。

想求前缀和6，我们要知道4，6；
想求前缀和5，我们要知道4，5；
这些数字怎么来的呢？

答：设想求前缀和x，则两个数字分别是x和x-lowbit(x).

前缀和6:lowbit(6)=2,6-2=4,故6 4
前缀和5:lowbit(5)=1,5-1=4,故5 4

也可以看这个：

树状数组的初始化

相关代码

//求2^x 
int lowbit(int x)
{
	return x&(-x);
}

//单点修改后的更新 
//这里的更新：如A[1]要加2，则y=2 
//版本1： 
void update(int x,int y,int n)//x为更新的位置，y为更新后的数，n为数组最大值 
{
	for(int i=x;i<=n;i+=lowbit(i))
	{
		c[i]+=y;
	}
}

//版本2：
void update(int x,int sum)
{
	while(x<=n)
	{
		d[x]+=sum;
		x+=lowbit(x);
	}
} 

//区间查询
//版本1： 
int getsum(int x)
{
	int ans=0;
	for(int i=x;i;i-=lowbit(i))
	{
		ans+=c[i];
	}
	return ans;
} 

//版本2：
int getsum(int x)
{
	int s=0;
	while(x>0)
	{
		s+=d[x];
		x-=lowbit(x);
	}
	return s;
} 

模板题和代码

洛谷P3374

题

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define fir(i,a,n) for(int i=(int)a;i<=n;i++) 
const int N=5e5+10;
int a[N];//这个是树状数组，原数组没有存 
int n,m;
int lowbit(int x)
{
	return x&(-x);
}

void update(int x,int sum)
{
	for(int i=x;i<=n;i+=lowbit(i))
	{
		a[i]+=sum;
	}
}

int getsum(int x)
{
	int ans=0;
	for(int i=x;i>0;i-=lowbit(i))//不能等于0！ 
	{
		ans+=a[i];
	}
	return ans;
}

int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++) 
	{
		int t;
		cin>>t;
		update(i,t);//构建树状数组 
	}
	
	for(int i=1;i<=m;i++)
	{
		int op,b,c;
		scanf("%d%d%d",&op,&b,&c);
		if(op==1)
		{
			update(b,c);
		}
		else if(op==2)
		{			
			cout<<getsum(c)-getsum(b-1)<<endl;
		}
	}
	return 0;
}

洛谷P3368

题：

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=500000+10;
ll c[N];//差分数组的树状数组 
int n,m;

int lowbit(int x)
{
	return x&(-x);
}
void update(int x,ll sum)
{
	for(int i=x;i<=n;i+=lowbit(i))
	{
		c[i]+=sum;		
	}
}
ll getsum(int x)
{
	ll res=0;
	for(int i=x;i;i-=lowbit(i))
	{
		res+=c[i];
	}
	return res;
}
int main()
{
	scanf("%d%d",&n,&m);
	ll now=0;
	memset(c,0,sizeof(c));
	for(int i=1;i<=n;i++)
	{
		ll t;cin>>t;
		update(i,t-now);
		now=t;
	}
	
	while(m--)
	{
		int op;scanf("%d",&op);
		if(op==1)
		{
			int x,y;ll k;scanf("%d%d%lld",&x,&y,&k);//如果是int k 再lld 就会死循环 
			//x-y +k --->update(x-1,k) (y+1,-k)
			update(x,k);
			update(y+1,-k);
		}
		else if(op==2)
		{
			int x;scanf("%d",&x);			
			cout<<getsum(x)<<endl;
		}
	}
	return 0;
}

这里有一个奇怪的错误：
在输入k的时候，如果int k，再lld，那么update函数就会出现0而死循环

我大为震撼

用树状数组求逆序对

举例子可以看这里：树状数组逆序对

树状数组的功能就是可以单点更新，区间查询，这样你把每个数该在的位置离散化出来，然后每次把每个数该在的位置上加上1，比如一个数该在的位置为x，那么用add(x)把这个位置加上1，然后再用区间查询read(x)查询1~x的和，也就是可以知道前面有多少个数是比他小的了（包括那个数自己），再用已经插入的数的个数减去read(x)，就算出了前面有多少个数比他大了。

模板题：题

题目描述
在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。比如一个序列为4 5 1 3 2， 那么这个序列的逆序数为7，逆序对分别为(4, 1), (4, 3), (4, 2), (5, 1), (5, 3), (5, 2),(3, 2)。

输入描述:
第一行有一个整数n(1 <= n <= 100000), 然后第二行跟着n个整数，对于第i个数a[i]，(0 <= a[i] <= 100000)。

输出描述:
输出这个序列中的逆序数

代码：注意要开LL！

#include<bits/stdc++.h>
using namespace std;
#define fir(i,a,n) for(int i=a;i<=n;i++)
typedef long long ll;
const int N=1e5+10;
int a[N],n;

int lowbit(int i)
{
	return i&-i;
}
void update(int x,int sum)
{
	for(int i=x;i<=n;i+=lowbit(i))
	{
		a[i]+=sum;
	}
}
int getsum(int x)
{
	int ans=0;
	for(int i=x;i;i-=lowbit(i))
	{
		ans+=a[i];
	}
	return ans;
}
int main()
{
	cin>>n;
	ll ans=0;
	fir(i,1,n)
	{
		int t;
		scanf("%d",&t);
		update(t,1);
		ans+=i-getsum(t);
	}
	cout<<ans;
	return 0;
}