
解此方程得到在均方误差最小意义下的拟合函数p(x),上述方程组称为多项式拟合的法方程,法方程的系数矩阵是对称的。当拟保多项式阶n>5时,法方程的系数矩阵是病态的,在计算中要用双精度或者一些特殊算法以保护解得准确性。
示例:给定一组数据,用二次多项式函数拟合这组数据

散点图如下所示:
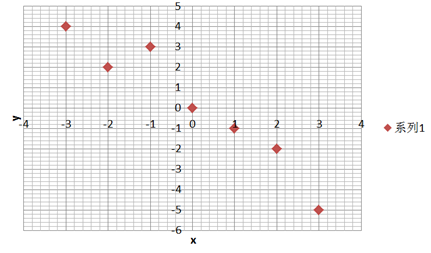
程序如下:
############################################
#Edit by wd,2013,4,16
############################################
import matplotlib.pyplot as plt
import numpy as np
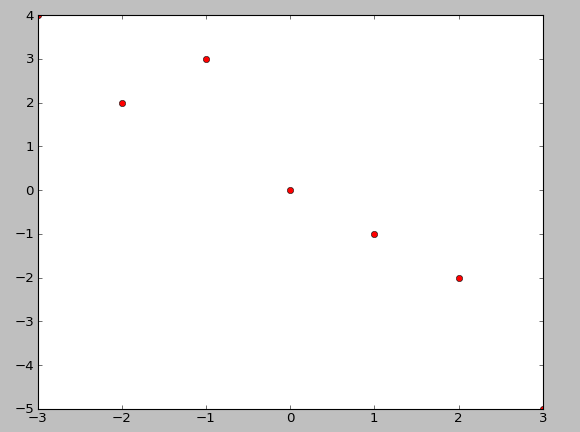
x = [-3,-2,-1,0,1,2,3]
y = [4,2,3,0,-1,-2,-5]
if len(x) != len(y):
exit
m = len(x)
def matrix_n(alist=[],n=0):
llen = len(alist)
r_list = [0]*llen
for i in range(llen):
r_list[i] = alist[i] ** n
return r_list
x_0 = [1]*m
x_2 = matrix_n(x,2)
x_3 = matrix_n(x,3)
x_matrix = np.matrix((x_0,x,x_2),dtype=np.int)
print x_matrix
y_matrix = np.matrix((y),dtype=np.int)
y_matrix = y_matrix.T
x_matrix_t = x_matrix.T
print x_matrix_t
out = ((x_matrix * x_matrix_t)** -1)*(x_matrix * y_matrix)
print out
'''
[[ 0.66666667]
[-1.39285714]
[-0.13095238]]
'''
plt.plot(x,y,"ro")
#plt.show()
xx = np.linspace(-5,5,5)
yy = -0.13095238*xx*xx + -1.39285714*xx + 0.66666667
plt.plot(xx,yy,label="$-0.13095238*xx*xx + -1.39285714*xx + 0.66666667$",color="red",linewidth=3)
plt.show()
拟合之后的图:
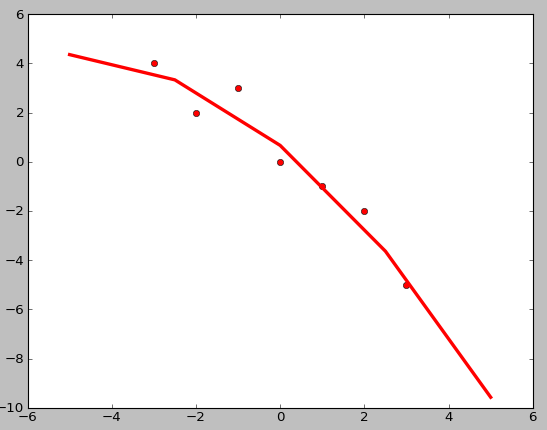








 本文介绍了一种使用二次多项式进行数据拟合的方法,并通过一个具体的实例展示了如何利用Python编程实现这一过程。该示例首先定义了一组数据点,然后通过构建相应的法方程来求解拟合参数,最后绘制了原始数据点与拟合曲线的对比图。
本文介绍了一种使用二次多项式进行数据拟合的方法,并通过一个具体的实例展示了如何利用Python编程实现这一过程。该示例首先定义了一组数据点,然后通过构建相应的法方程来求解拟合参数,最后绘制了原始数据点与拟合曲线的对比图。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








