（四）1.自动控制原理 The Root Locus Method 根轨迹基本概念

上一章我们说了时域的分析，这一章我们说说频域的分析

---

根轨迹法定义和初步认识

---

根轨迹法是靠图像的方法直观得分析，缺点是不太准确
使用范围是观察在系统中某个参数变化对系统的影响

具体来说，根轨迹就是当系统中的某个参数从0到无穷变化时，他的根的变化情况，按照轨迹绘制表格，就是根轨迹法的要义了

对于一个开环传递函数：
当化成尾一型时，前面的系数就是开环增益
化成首一型时，得到的就是根轨迹增益（没有开环闭环之分，只对开环而言）

---

零极点总览

---

给定一个简单系统，去看开环闭环零极点的情况
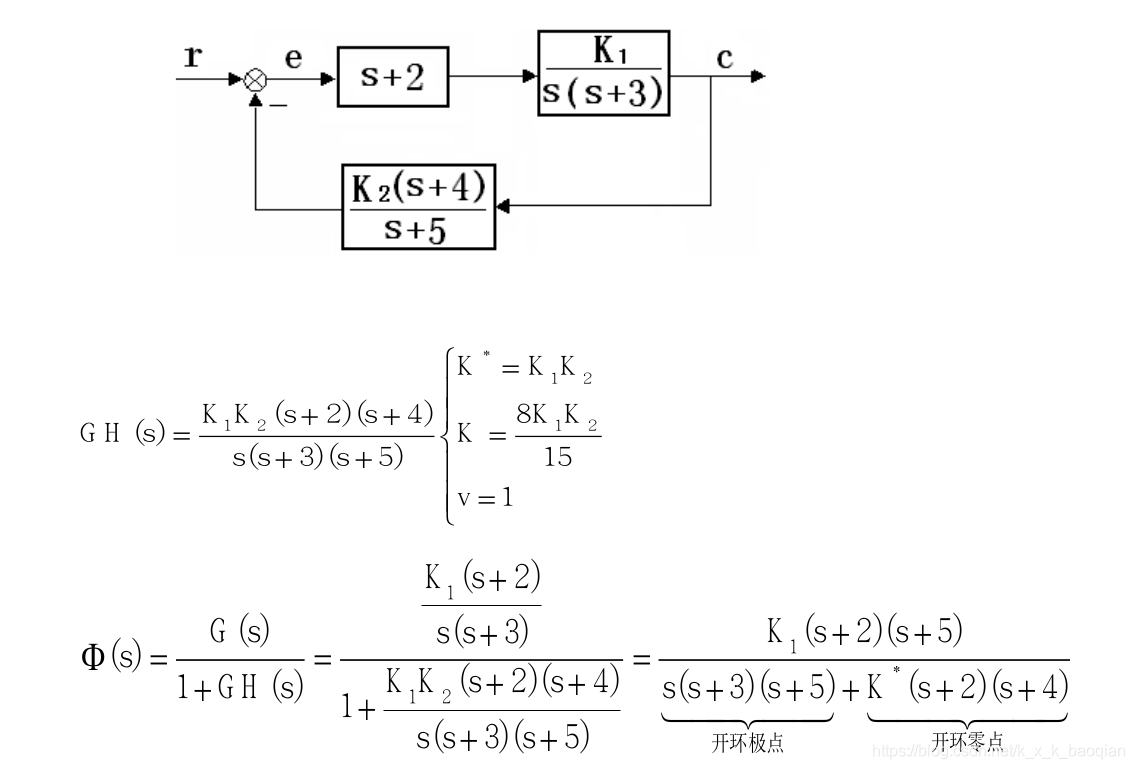注意求增益，所说的首一尾一是同时对分子分母而言

闭环零点 = 开环零点 + 反馈路径上的极点（过于简单）
闭环极点和  开环零极点，根轨迹增益都有关（研究对象）

---

根轨迹方程

---

对一个系统，求出闭环传递函数，令其分母等于0，即是根轨迹方程

那我们怎么去判断一个点是不是根轨迹上的点？
根据复变函数的思想，确定一个点位置，靠的是下面这两个参数

1.模值
2.相角

一般公式如下：

注意：
1.模值条件永远满足，因为根轨迹增益不确定，是可以变的
2.满足相角条件的点都是根轨迹增益上的点，再靠1.条件去确定根轨迹增益

判断一个点是否为根轨迹上点的一般步骤

1.找到闭环函数所有的极点和零点
所有分子到这个点矢量相角之和（零点） - 所有分母到这个点矢量相角之和（极点） =pai×（2k+1）
如果满足，则是轨迹上点
2.令模等于1，求出K'