基于参考价格效应的医疗保险策略实现医疗供应链网络协调

摘要
中国已建立了全民医疗保险系统,个人自付费用有所下降,但中国居民的人均医疗支出和社会整体医疗费用却大幅增加。阻碍中国社会医疗体系实现可持续发展的一个主要挑战是医院住院人数分布不均:上级医院人满为患,而下级医院则就诊人数偏低。本文应用博弈论模型来协调由政府、医疗保险基金、上级医院、下级医院和患者组成的医疗供应链网络。特别是通过考虑参考价格效应,本文分析了不同的医疗保险报销策略及其对患者选择和医疗供应链网络的影响。研究结果表明,参考价格效应增强了医疗保险的杠杆作用,引导了患者选择,优化了医疗资源的分配,并降低了医疗支出。与分散决策策略相比,集中决策策略能够激发上级医院和下级医院的合作意愿,有利于社会医疗体系的发展。
关键词 : 医疗供应链网络;医疗保险报销策略;参考价格效应;博弈论;患者选择行为
1. 引言
中国自2011年以来已成功实现全民医疗保险覆盖,这是人类历史上规模最大的保险覆盖扩展[1]。医疗费用中自付比例从2011年的34%下降至2018年的15%。然而,患者的平均支出从187.8元上升至268.3元,医疗总费用从2011年到2018[2]期间增长了28.3%。另一方面,由于中国经济的快速发展,公民的健康意识日益增强,对高质量医疗服务的需求强烈。在中国,医疗供应链网络由政府、医疗保险基金、医疗机构和患者组成。医疗机构分为上级医院和下级医院[3]。上级医院在多个方面相较于下级医院具有优势,例如先进的医疗设备和医生的专业能力。值得注意的是,患者可以自由选择就诊医院。无论所患疾病类型如何,患者往往倾向于选择上级医院,导致上级医院人满为患。因此,下级医院的入院率较低[4,5]。事实上,对于患有常见疾病的患者而言,无需前往上级医院就诊,因为在下级医院即可获得适当的治疗。此外,由于上级医院对同一项医疗服务的收费高于下级医院[6],导致医疗总费用增加。所有这些情况反映了整个医疗系统在效率和公平性方面存在的严重社会问题[7]。
最重要的因素是医疗资源分配不均,且医疗供应链网络参与者之间的合作尚未建立。因此,由于缺乏标准化,患者面临困境,阻碍了他们做出知情决策的能力。因此,有必要通过提高医疗服务的可及性、降低医疗服务成本以及实施医疗资源的合理分配来解决这一问题。
医疗保险是优化资源配置和协调医疗体系的有效工具,通过设置不同的报销策略还可以引导患者选择[8]。医疗保险可以通过报销帮助降低患者的费用,减轻患者的医疗负担,并解决医疗服务高成本的问题[9]。在考虑医疗保险报销策略时,有两个基本规则:第一,根据医疗政策针对不同疾病设定不同的报销标准[10];第二,根据不同医疗机构设定不同的报销比例[11,12]。政府对报销的使用以及医疗供应链网络的整体利润进行监管,同时在制定保险策略时充分考虑总保险支出。通过这种方式,可以在最低保险支出下获得最优医疗效益[5],因此应根据不同医院的医疗服务情况制定不同的医疗保险政策,这不仅有利于不同医院的发展,还能限制患者选择,从而实现控制医疗费用的目的。
在新医改政策的指导下,医疗保险不再仅仅是一种报销手段,更是协调整个医疗供应链网络的有力工具。医疗保险报销可以促进两家医疗机构之间的纵向合作,优化资源配置,实现资源共享和优势互补,有效降低医疗服务成本并提高患者效用[13–15]。
因此,实施医疗保险报销策略以促进医疗资源的合理利用并协调医疗供应链网络,是一个值得我们关注的研究方向。尽管过去几十年来医疗保险报销策略已得到广泛研究,但在医疗供应链网络中尚未考虑参考价格效应这一重要的营销现象。参考价格是消费者对某产品的价格预期,源于消费者的购买经历、产品价格信息或其他非价格因素。参考价格的直接影响是形成消费者的感知价格。消费者在做出购买决策时通常具有特定的心理参考价格。参考价格对消费者决策的影响体现在以下方面:当消费者欲购买某种商品时,若该商品的市场价格低于其心理参考价格,其内心的获利感将促使其购买;反之,若市场价格高于心理参考价格,消费者则会因损失感而拒绝购买。在医疗系统中,参考价格效应同样存在。医疗参考价格体系已在多数国家付诸实践,并被证明是报销标准管理的有效手段。例如,德国于1989年实施医疗改革法案,在其法定医疗保险体系中率先推行一体化定价与补偿——即参考价格体系。该参考价格体系通过调整医疗保险报销水平以及提高患者对价格的敏感性,间接控制医疗服务价格。此外,参考价格效应提高了需求弹性以及供应商市场的竞争,从而导致医疗服务成本的降低。
参考价格为患者、医院和政府之间提供了参考标准和依据。
2. 文献综述
2.1. 医疗供应链网络
医疗供应链网络是一个热门话题,近年来许多研究人员对此领域产生了浓厚的兴趣。医疗供应链网络由多种产品和服务企业构成,包括医疗耗材、药品、餐饮、废物管理、信息技术、车辆fleet管理、通用物资[13],主要参与者包括政府、医院、医生与患者[8]。由于供应链在医疗行业中的关键作用,文献中已提出了不同的方法以实现成本降低[14]。此外,关于运营管理和供应链管理在医疗领域的研究仍然具有现实意义。这两个领域的大多数研究依然着眼于正常情况下的供应链运营和技术[16]。
关于医疗供应链网络的研究通常采用博弈论构建理论模型,以分析各参与者的行为和利益[27]。Sinha等人[28]构建了一个关于医疗质量和医疗成本的博弈模型,并提出了一种医疗保险策略,该策略能够鼓励医疗服务提供者降低成本并避免额外补偿。Gardner等人[29]运用博弈论分析了新型农村合作医疗保险的主体,发现激发患者参与的积极性以及加强患者行为的监督是新医疗政策成功的关键。Landry等人[30]研究激励理论,探讨医疗保险激励的可行性,并认为医疗保险报销应充分考虑患者的心理可接受性,以提高下级医院就诊率以及医疗服务的可及性和可用性。综上所述,从这些研究可以推断,引入博弈论作为战略工具,可在医疗供应链网络组织层面产生积极影响效应[31]。对国内外关于纵向供应链协调的文献回顾表明,大多数研究从理论视角建立相关数学模型,并采用博弈论方法进行分析[32]。
在协调医疗供应链网络方面,医疗保险报销是一项基本工具。通过讨论不同的策略以促进纵向合作、优化资源分配、实现资源共享和优势互补,有效降低医疗服务成本并提高服务质量[16,33,34]。Lillrank等[35]认为医院通常采用不同的价格控制策略,并利用模型分析患者对优质护理的选择。钟等[36]指出,医疗保险的目标应定位于常见病和多发病,以提高农村基本医疗和卫生体系的可及性和可用性,特别是降低治疗成本。Jayaram等[37]发现,当医疗服务边际成本较高时,医疗保险的存在能够增加患者效用。
目前,与医疗供应链网络中医疗机构的横向竞争相比,纵向合作已受到广泛关注。张等人[11]通过建立企业间的纵向合作模型,研究了上下游企业服务成本分担策略对整个供应链利润的影响。Lehoux等人[38]相继研究了垂直整合和纵向结构对上下游企业合作以及整个供应链利益的影响。曹、万等人[39]研究了绿色供应链中的纵向合作策略,并分析了在不同策略下相同政府支出的报销效果。Jaber等人[40]讨论了在不同消费者策略下供应链各成员的竞争与合作理论。Samuel等人[14]通过调查双边垄断市场结构,指出了差异化产品垂直整合所引发的问题。在考虑财政报销政策的基础上,Panda等人[41]系统地比较和讨论了三种类型供应链中制造商与供应商合作的博弈模型。此外,当前大多数博弈论研究模型均基于静态合作[42],而为了实现更科学的供应链协调,研究动态合作的纵向供应链模型[43]具有重要意义。
2.2. 医疗保险
中国在2011年成功实现了全民医疗保险覆盖,这是人类历史上规模最大的保险覆盖扩展。在发展中国家中,实现全民医疗保险覆盖的情况极为罕见,然而拥有13亿人口的最大发展中国家——中国却实现了这一[4]。中国的成就令人瞩目,但仍面临严峻挑战。以下简要介绍中国的医疗保险政策,以帮助更好地理解本文的研究背景。医疗保险的首要目标是减轻患者所面临的财务风险。根据中国卫生部部长的说法,即使有了医疗保险覆盖,财务风险仍然很高[44]。为解决这一问题,政府已提高了公共保险报销金额,旨在将自付费用降低至医疗卫生总支出的30% 2018[45]。医疗保险的主要目标旨在提高医疗服务质量。政府已加大了对医疗卫生系统投资,但效果尚不明确。由于中国人民的收入增长,人们对更高质量的医疗服务产生了强烈需求。为满足这一需求,应提高医疗服务质量[46]。医疗保险被用作协调医院报销的工具,以增加收入,从而提升医疗质量[47]。
在中国,存在三种基本的公共医疗保险制度:新型农村合作医疗制度(NRCMS)、城镇居民基本医疗保险(UBMI)和城镇职工基本医疗保险(UEBMI)[48]。2016年1月,国务院发布了关于将NRCMS和UBMI整合为城乡居民统一的基本医疗保险制度(URBMI)的意见[49]。下一步,政府将建立并完善医疗保险制度之间的衔接与整合,逐步统一为公民基本医疗保险(CBMI)[50]。由于频繁的身份变化,除卫生部门外,民政部门及其他相关部门将建立协调机制,促进各项制度的融合与整合。此外,政府已提高了城乡居民医疗保险的报销比例。2019年5月13日,国家医疗保障局和财政部发布了关于确保城乡居民基本医疗保障的通知,要求稳步提高[25]。城乡居民医保报销比例从50%提高到60%,未来有望为所有公民建立相同的报销比例[24,51]。
2.3. 参考价格
研究人员关注医疗供应链体系和医疗保险,但作为整个系统需求来源的基本参与者——患者,却未被讨论。患者选择是医疗供应链网络协调的最重要因素。而影响患者选择的重要因素之一——参考价格效应,尚未被考虑在内[52]。参考价格自20世纪80年代以来已被研究,现已成为心理学和市场营销领域中的成熟理论[53]。班鲍尔[54]指出,参考价格框架与多种消费者行为和价格感知的心理学理论一致,包括适应水平理论和同化对比理论。参考价格对消费者选择、产品定价以及整个供应链的协调至关重要[20]。戴等人[17]认为,消费者在做出购买决策时通常具有特定的参考价格。一种常见的概念化观点认为,参考价格是一种由消费者的先前经验和当前购买环境所形成的预测性价格预期。正如崔[55]所指出的,参考价格代表了消费者对产品的评价,并受到多种因素的影响,如价格(包括历史价格、建议零售价、竞争产品价格等)、数量、广告等。根据马祖姆达尔等人[52]的观点,参考价格对消费者需求的影响可能源于参考价格与当前市场价格之间的动态比较。徐等人[56]进一步提出,实际价格高于或低于参考价格会对消费者产品评价产生不同的影响。
大量研究探讨了参考价格效应对消费者购买和企业运营策略的影响,以及如何测量或建模[52,53]。参考点的概念还被扩展到其他刺激因素,如价格促销和产品质量[57]。一些研究人员还利用经济理论和博弈论建立了消费者选择模型[18,58]。另一些研究则在对企业竞争行为的建模中考虑了参考价格效应,并为零售商和制造商制定了管理指南[59]。尽管参考价格概念具有重要意义,但目前尚缺乏一个全面的框架来系统地研究其在医疗供应链网络中的影响。
在医疗行业中,参考价格效应将直接影响患者的就医决策,是患者选择医院的关键因素[54,60]。因此,将参考价格效应引入医疗供应链网络纵向协调的创新模型中,有助于参与者做出更加科学合理的决策。
3. 问题描述与模型构建
3.1. 问题描述
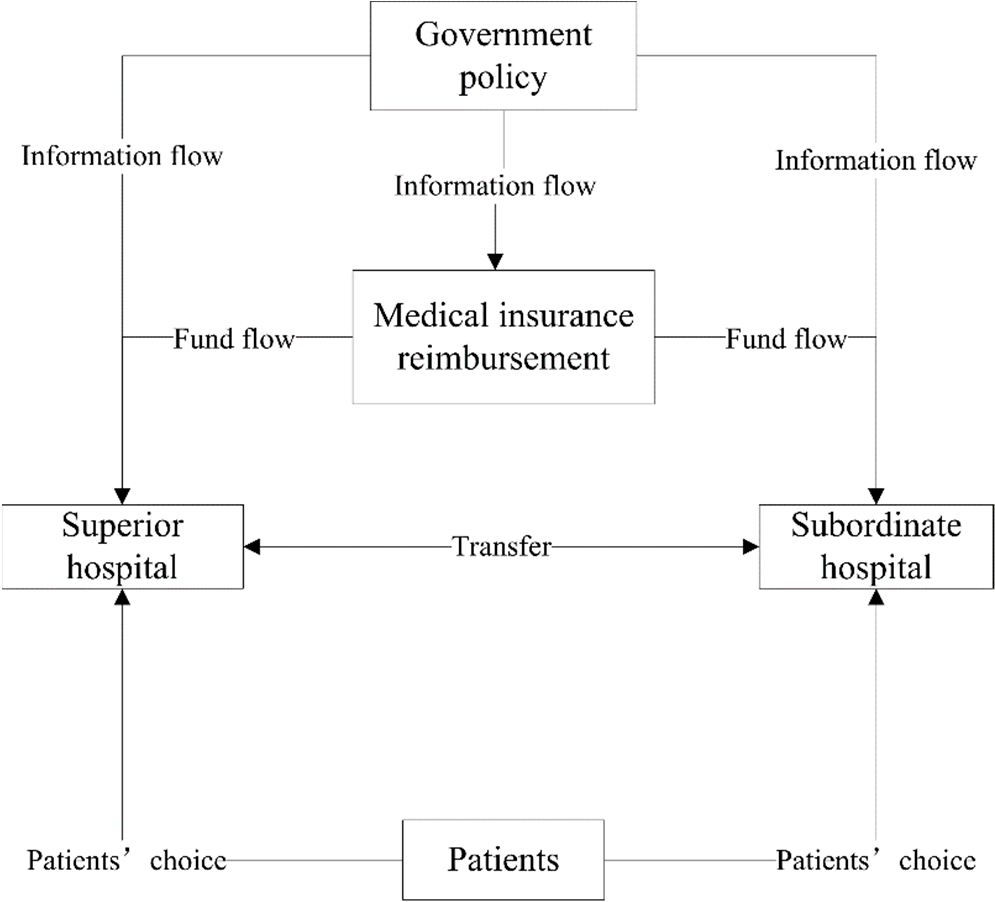
本节构建了一个由政府、医疗保险基金、医疗机构(包括上级医院和下级医院)以及患者组成的医疗供应链网络。该网络如图1所示。政府对整个医疗系统进行整体管理,并制定医疗保险报销政策。医疗服务的公共品性质决定了政府参与基本医疗服务供给的必要性。作为医疗保障体系的管理者,政府为医疗保障体系提供政策支持和财政支持,并有效监管医疗市场[61]。2009年,新医改方案明确了政府在基本医疗服务中的主导作用[62]。作为医疗服务的购买方和医疗活动的监督者,医疗保险机构是医疗服务交易中的重要环节,也是推动整个医疗卫生体系改革的重要杠杆。
患者是医疗服务的消费者,他们推动着医疗服务供应链的发展。因此,患者效用满意度是一个重要的用于健康服务供给绩效评估的指标服务供应链[63]。提供满意的为患者提供医疗服务是所有节点的目标医疗服务供给链。卫生服务供应链从患者的需求开始,促进t he flow of l 物流、信息流和资金流,最终使患者能够获得高质量、安全且有效的医疗卫生服务[64]。然而,由于医疗服务市场中医生与患者之间存在信息不对称,掌握更多专业信息的医生和医院处于主导地位,而患者则处于被动地位,只能依赖医疗服务提供者来决定其对医疗服务的购买[65]。患者没有主动议价权,但可以决定选择哪家医院。当患者决定就诊的医疗机构时,医疗服务质量和服务价格是他们考虑的两大主要因素[15]。然而,由于患者对两级医疗机构之间的差异具有主观认知,通常会认为上级医院具有更好的治疗效果,即使上级和下级医院均具备治疗相同疾病的能力。因此,患者对上级医院的可接受参考价格将远高于下级医院[66]。
在新医改政策下,政府通过调整医疗保险报销策略引导患者选择合理的医疗机构,以期最大化各方利益。因此,政府要求上级医院通过医疗保险对下级医院提供一定的支持补贴,以促进患者分流,充分有效利用医疗资源[67]。最终,根据不同医疗机构的医疗保险报销、医疗服务价格以及对治疗效果的预先判断,患者形成心理参考价格,并选择能够使自身利益最大化的医院。
3.2. 基准模型构建
根据张[68]的观点,消费者会根据自身的记忆效应和心理认知调整其参考价格。参考价格函数如下所示(.r(t)= dr(t) dt):
$$ r.(t)= \gamma(p(t)-r(t)), r(0)= r_0 \quad (1) $$
其中,$ r(t) $ 为参考价格,$ p(t) $ 为当前价格,表示患者完成治疗过程所需支付的平均医疗服务价格(包括药费、诊疗费等),$ t \in [0,+\infty) $ 为患者前往医院的特定时间。$ \gamma $ 表示患者记忆效应的影响。$ 0 \leq \gamma \leq 1 $,$ \gamma $ 越大,表明消费者具有短期记忆,且对该选择的满意度越低。$ r(0)= r_0 $ 为常数,通常受患者满意度、医疗服务质量及类似价格等因素影响。
政府为上级医院设定的现行医疗保险报销策略为 $ S_h(t) $,为下级医院设定的现行医疗保险报销策略为 $ S_b(t) $。在新医改政策下,由于保险报销的影响,患者的心理参考价格将略有上升,因此患者参考价格函数被重新定义为:
$$ r.(t)= \gamma(p(t)-r(t))+ \theta_bS_b(t)+ \theta_hS_h(t), r(0)= r_0 \quad (2) $$
其中,$ \theta_b $ 和 $ S_b $ 分别表示下级和上级医院报销对参考价格的影响。通常,医疗保险报销方面的投资能够提升医院形象,从而进一步提高消费者对其服务质量的评价[53]。因此假设 $ \theta_h > 0 $ 且 $ \theta_b > 0 $ 成立。基于此,得到考虑参考价格效应的医疗供应链网络中的患者就诊需求函数:
$$ D(t)= \alpha - \beta p(t)+ \delta[r(t)-p(t)+ \theta_hS_h(t)+ \theta_bS_b(t)] \quad (3) $$
$ D(t)= \alpha - \beta p(t) $ 表示在没有参考价格效应的情况下,医疗服务市场中患者的需求。$ \alpha > 0 $ 表示潜在市场容量,$ \beta > 0 $ 表示需求价格弹性。$ \delta > 0 $ 表示参考价格对需求的影响。$ \delta $ 越大,表明患者对参考价格与实际医疗服务价格[55]之间的差距越敏感。在特殊情况下,$ \delta = 0 $ 表示不考虑参考价格效应。
医疗保险中上级医院和下级医院的成本函数分别设为 $ C_h= \frac{1}{2} \eta_hS_h(t)^2 $ 和 $ C_b= \frac{1}{2} \eta_bS_b(t)^2 $($ \eta_h \geq 1 $ 和 $ \eta_b \geq 1 $ 分别为上级医院和下级医院各自效率的逆向度量系数)[69,70]。
在具有参考价格效应的医疗供应链网络中,患者的心理价格在决策时受到记忆效应的影响,即患者在选择医疗机构时,不仅取决于当前状态,还取决于过去的经历[55]。患者的效用函数为:
$$ U= U(x)+ . r(t)+ F(t) \quad (4) $$
患者具有拟线性偏好[17],函数(4)可以重写为:
$$ U= \ln(x)+r.(t)+ F(t) \quad (5) $$
其中 $ x $ 表示患者的资产,$ x= w-p+ \theta s(t) $,$ w $ 表示患者的初始资产,并服从[0, W]上的均匀分布。$ F(t) $ 表示患者在时刻的健康状况,$ F \in [0, 1] $,0表示患者处于生病状态,1表示患者健康。$ F_0(t)= 0 $ 表示患者不去看医生。
同时,除了患者选择外,政府还引导上级和下级医院签订关于二次分配的协议。上级医院向下级医院提供一定的财政补贴和技术支持,以有效缓解其医疗资源短缺状况,并提升整体医疗保健效益。
假设上级和下级医院的平均边际利润分别为 $ \rho_h $ 和 $ \rho_b $。设定 $ \phi \in [0, 1) $ 为二次分配的具体比例系数,则上级和下级医院的利润函数为:
$$ \pi_h= \int_0^\infty e^{-\varphi t}(\rho_hD_h(t)- \frac{1}{2}\eta_hS_h^2(t)- \frac{1}{2}\phi\eta_bS_b^2(t))dt \quad (6) $$
$$ \pi_b= \int_0^\infty e^{-\varphi t}(\rho_bD_b(t)- \frac{1}{2}(1-\phi)\eta_bS_b^2(t))dt \quad (7) $$
其中 $ \varphi > 0 $ 表示相应的折扣率。然后,医疗供应链网络的总利润函数为:
$$ \pi_{sc}= \int_0^\infty e^{-\varphi t}((\rho_hD_h+ \rho_bD_b)- \frac{1}{2}\eta_hS_h^2(t)- \frac{1}{2}\eta_bS_b^2(t))dt \quad (8) $$
现在我们构建动态博弈模型,并利用哈密顿函数来优化整个供应链系统。基于方程(6)和(7),医疗供应链网络中上下级医院的哈密顿函数如下:
$$ H_h= \rho_h(\alpha - \beta p+ \delta(r-p)+ \theta_hS_h+ \theta_bS_b)- \frac{1}{2}\eta_hS_h^2 - \frac{1}{2}\phi\eta_hS_b^2+ \nu_h(\gamma(p-r))+ \theta_hS_h+ \theta_bS_b \quad (9) $$
$$ H_h= \rho_h(\alpha - \beta p+ \delta(r-p)+ \theta_hS_h+ \theta_bS_b)- \frac{1}{2}(1-\phi)\eta_hS_b^2+ \nu_h(\gamma(p-r))+ \theta_hS_h+ \theta_bS_b \quad (10) $$
其中 $ v_h $ 和 $ v_b $ 分别为伴随变量,表示参考价格对上级和下级医院收入的影响。本文所用的相关符号说明见表1。
| 参数 | 描述 |
|---|---|
| $ r(t) $ | 患者的参考价格 |
| $ p(t) $ | 单位服务价格 |
| $ t $ | 患者前往医院的特定时间 |
| $ \gamma $ | 患者记忆效应的影响 |
| $ S(t) $ | 医疗保险报销 |
| $ x $ | 患者的资产 |
| $ w $ | 患者的初始资产 |
| $ \theta $ | 医疗保险报销对参考价格的影响 |
| $ D(t) $ | 患者咨询需求 |
| $ \alpha $ | 基础市场规模 |
| $ \beta $ | 需求价格弹性 |
| $ \delta $ | 参考价格对需求的影响 |
| $ \rho $ | 平均边际收益 |
| $ C $ | 医疗保险成本 |
| $ \eta $ | 各自效率的逆测量系数 |
| $ U $ | 患者效用 |
| $ F $ | 患者健康状况 |
| $ \phi $ | 二次分配的特定比例系数 |
| $ \pi $ | 利润 |
| $ \varphi $ | 相应的折扣率 |
| $ n $ | 实际患者入院人数 |
| $ v $ | 伴随变量 |
上标ns、ss、cs分别表示博弈论中纳什、斯塔克尔伯格和集式模型下的医疗保险策略。下标b、h分别表示上级医院和下级医院。
4. 模型分析
4.1. 分散决策模型
在分散决策模型中,政府根据医院的最优决策制定医疗保险报销政策,以最大化各自的利益[71]。
4.1.1. 纳什均衡策略(NS)
在此策略中,上级医院和下级医院彼此不了解对方的决策。双方同时采取行动,并获得各自的最优决策以最大化自身利益,符合纳什均衡博弈条件。在此过程中,上级医院的医疗保险报销为 $ S_{ns}^h $,下级医院的医疗保险报销为 $ S_{ns}^b(t) $。
利用动态规划的最优控制理论,我们可以得到如下解:
命题1 。上级医院的医疗保险报销最优纳什均衡策略为:
$$ S_{ns}^h(t)= \frac{1}{n_h}(\theta_h\rho_h+ \theta_h\delta\rho_h \varphi+ \gamma) \quad (11) $$
同理,下级医院的医疗保险报销为:
$$ S_{ns}^b(t)= \frac{1}{n_b}(\theta_b\rho_b+ \theta_b\delta\rho_b \varphi+ \gamma) \quad (12) $$
证明 :对方程(9)中的 $ S_h $ 求一阶偏导数,并令其等于零:
$$ \frac{\partial H_h}{\partial S_h} = 0 \Leftrightarrow \eta_hS_h= \theta_h\rho_h+ \theta_h\nu_h \quad (13) $$
其中:
$$ . \nu= \varphi\nu_h - \frac{\partial H_h}{\partial r} =(\varphi+ r)\nu_h -\delta\rho_h \quad (14) $$
求解方程(14),我们得到以下通解:
$$ \nu_h= Ae^{(\varphi+\gamma)t}+ \frac{\delta\rho_h}{\varphi+ \gamma} \quad (15) $$
$ A $ 是待定参数,如果 $ A, 0 $,则 $ v_h $ 将随时间趋于无穷大,这与实际情况不符,因此 $ A= 0 $。在 NS策略中,不存在合作,因此 $ \phi= 0 $。
将公式(15)代入公式(13),可得:
$$ S_{hns}(t)= \frac{1}{\eta_h}(\theta_h\rho_h+ \theta_h\frac{\delta\rho_h}{\varphi+ \gamma}) \quad (16) $$
同样,考虑公式(10),解为:
$$ S_{ns}^b(t)= \frac{1}{\eta_b}(\theta_b\rho_b+ \theta_b\frac{\delta\rho_b}{\varphi+ \gamma}) \quad (17) $$
根据对命题1的分析,可以得出以下结论:从表2和3可以看出,$ S_{ns}^b $ 与 $ \theta_b $ 呈正相关,且 $ S_{ns}^h $ 与 $ \theta_h $ 呈正相关。同时,$ S_{ns}^h $ 和 $ S_{ns}^b $ 均与 $ \delta $ 呈正相关。这意味着随着参考价格效应的增强,医疗保险报销会增加,对溢价的认知将得到缓解,从而解决了就医高成本的问题。
| 参数 | $ \theta_h \uparrow $ | $ \delta \uparrow $ | $ \rho_h \uparrow $ | $ \eta_h \uparrow $ |
|---|---|---|---|---|
| 报销 $ S_{ns}^h $ | ↑ | ↑ | ↑ | ↓ |
表2 。上级医院医保报销与参数之间的关系。
| 参数 | $ \theta_b \uparrow $ | $ \delta \uparrow $ | $ \rho_b \uparrow $ | $ \eta_b \uparrow $ |
|---|---|---|---|---|
| 报销 $ S_{ns}^b $ | ↑ | ↑ | ↑ | ↓ |
表3 。下级医院医保报销与参数之间的关系。
由于 $ S_{ns}^h $ 与 $ \rho_h $ 呈正相关,且 $ S_{ns}^b $ 与 $ \rho_b $ 呈正相关,因此医疗保险报销可提高边际收益。$ S_{ns}^h $ 与 $ \eta_h $ 呈负相关,这意味着其与医院服务效率呈正相关,$ S_{ns}^b $ 与 $ \eta_b $ 也是如此。该结论表明,医疗保险报销能够提升医院服务效率,并减少患者等待时间。
4.1.2. 斯塔克尔伯格策略分析(SS)
我们认为,由于上级医院是高级医疗机构,在医疗保险报销策略的决策中具有主导地位和决策优先权,符合斯塔克尔伯格博弈论条件。在此过程中,上级医院的医疗保险报销为 $ S_{ss}^h(t) $,下级医院的医疗保险报销为 $ S_{ss}^b(t) $。下级医院的报销率为 $ \phi $。
根据方程(9)和(10),利用动态规划的最优控制理论,我们得到斯塔克尔伯格博弈中 $ S_{ss}^h(t) $ 和 $ S_{ss}^b(t) $ 的均衡解,如下述命题所示:
命题2 :在斯塔克尔伯格博弈论中,上级医院的最优医疗保险报销为:
$$ S_{ss}^h(t)= \frac{1}{\eta_h}(\theta_h\rho_h+ \theta_h\frac{\delta\rho_h}{\varphi+ \gamma}) \quad (18) $$
类似地,下级医院的最优医疗保险报销为:
$$ S_{ss}^b(t)= \frac{1}{\eta_b(1 -\phi)}(\theta_b\rho_b + \frac{\theta_b\delta\rho_b}{\varphi+ \gamma}) \quad (19) $$
命题2 Proposition 2的证明与Proposition 1的证明类似。
根据命题2中的斯塔克尔伯格均衡解,可以找到下级医院的最优医疗报销率,如命题3所示。
命题3 :在斯塔克尔伯格博弈论中,下级医院的最优报销率为:
$$ \phi= \begin{cases} \frac{2\rho_h-\rho_b}{2\rho_h}, & 2\rho_h> \rho_b \ 0 & \text{others} \end{cases} \quad (20) $$
证明 :将方程(18)和方程(19)代入方程(2),可得:
$$ r.(t)= \frac{dr(t)}{dt}= \gamma(p-r)+ \theta_hS_{ss}^h+ \theta_bS_{ss} \quad (21) $$
求解方程(21),我们得到其通解:
$$ r(t)= C_0e^{-\gamma t}+ r_{sss} \quad (22) $$
其中 $ r_{sss}= p’+(\theta_hS_{ss}^h’+ \theta_bS_{ss}^b’)/\gamma $
设 $ t= 0 $ 并结合方程(22),我们得到:
$$ r_0= C_0+ r_{sss} \Leftrightarrow r_0 -r_{sss} \quad (23) $$
然后,将方程(22)代入上级医院的利润函数(6)中,以获得 n:
$$ \pi_h= \rho_h \left(\alpha -\beta p+ \delta(r_{sss} -p)+ \theta_hS_{ss}^h+ \theta_bS_{ss}^b \frac{}{\varphi} + \frac{\delta C_0}{\varphi+ \gamma} \right)- \frac{\eta_hS_{ss}^h -\phi\eta_bS_{ss}^b}{2\varphi} \quad (24) $$
将方程(18)和方程(19)代入方程(24),并对其求一阶偏导数,然后令其等于零:
$$ \frac{d\pi_h}{\phi} = 0 \Leftrightarrow \phi= \frac{2\rho_h -\rho_b}{2\rho_h} \quad (25) $$
最后,我们将 $ \phi \in [0, 1) $ 的定义域结合,得到下级医院的最优报销率。
命题3表明,在斯塔克尔伯格博弈论中,上级医院的医疗保险报销 $ S_{ss}^h(t) $ 保持不变,而下级医院的报销率 $ \phi $ 主要基于双方参与者的边际收益 $ \rho_h, \rho_b $。
4.2. 集中决策模型(CS)
在集中决策模型中,政府制定医疗保险报销政策以最大化整个医疗供应链网络的整体利益[72]。在当前医疗联合体垂直整合的供应链结构下,如果在医疗政策项目上达成了具有约束力的合作协议,则医疗供应链网络中的上级和下级医院将进行协调[41]。然后,我们采用集中决策模型,并根据公式 (8),其哈密顿函数为:
$$ H_{sc}=(\rho_h+ \rho_b)(\alpha -\beta p+ \delta(r-p)+ \theta_hS_h+ \theta_bS_b)- \frac{1}{2} \eta_hS_h^2 - \frac{1}{2} \eta_bS_b^2 + \nu_{sc}(\gamma(p-r)+ \theta_hS_h+ \theta_bS_b) \quad (26) $$
其中 $ v_{sc} $ 是一个协态变量,表示参考价格效应对供应链的影响。根据公式(26),利用最优控制理论和动态规划,我们得到上下级医院的最优医疗保险补贴,如命题4所示。
命题4 :在集中决策模式下,上级医院的医疗保险报销为:
$$ S_{hcs}(t)= \frac{1}{\eta_h}(\theta_h(\rho_h+ \rho_b))+ \frac{\theta_h\delta(\rho_h+ \rho_b)}{\varphi+ \gamma} \quad (27) $$
同样,下级医院的医疗保险报销为:
$$ S_{cs}^b(t)= \frac{1}{\eta_b}(\theta_b(\rho_h+ \rho_b))+ \frac{\theta_b\delta(\rho_h+ \rho_b)}{\varphi+ \gamma} \quad (28) $$
命题4的证明与命题1的证明类似。
根据上述结果,当在供应链的集中决策模型中考虑参考价格效应时,医疗保险对上级和下级医院的报销金额取决于患者的参考价格以及医疗机构的边际利润值。与分散决策模型不同,在医疗系统的垂直整合中,各医疗机构在决策时会考虑其上下游关联机构的边际收益,从而提升医疗供应链网络的协调性。
因此,命题4表明,在供应链协调中,医疗服务保险报销不仅取决于参考价格效应,还取决于所有合作医疗机构的边际利润。通过这种方式,我们可以促进医疗机构的整合,并最大化整个医疗供应链网络的利益。
5. 医疗保健供应链网络协调
5.1 医疗供应链网络中的患者选择
患者根据自身的效用做出医疗服务选择。根据公式(5):患者不就医的效用为:
$$ U_0= \ln(x)+ r.(t)+ F_0(t) $$
患者选择下级医院的效用为:
$$ U_b= \ln(x)+ . r(t)+ F_b(t) $$
选择上级医院的患者效用为:
$$ U_h= \ln(x)+ . r(t)+ F_h(t) $$
对患者行为的分析如下:
1) 患者不去看病的情况。
显然,$ F_b(t) $ 和 $ F_h(t) $ 大于 $ F_0(t) $,因此 $ U_0 $ 小于 $ U_b $ 和 $ U_h $,这意味着当人们生病时,他们会选择去看医生。
2) 患者选择下级医院的情况。
在这种情况下,患者的效用函数应满足 $ U_b > U_h $,即:
$$ \ln[w-p_b+ \theta_b s_b(t)]+ . r(t)+ F_b(t)> \ln[w-p_h+ \theta_h S_h(t)]+ . r(t)+ F_h(t) \quad (29) $$
$$ \Rightarrow \ln\left[\frac{w-p_b+ \theta_b S_b(t)}{w-p_h+ \theta_h S_h(t)}\right]> F_h(t)-F_b(t) \quad (30) $$
由于患者具有先验主观性,他们认为对于相同的医疗服务,上级医院的服务质量优于下级医院,因此设定 $ F_h(t) -F_b(t)= a $ 且 $ 0< a< 1 $,则可得:
$$ w< \frac{e^a[p_h -\theta_h S_h(t)]-p_b+ \theta_b S_b(t)}{e^a -1} $$
患者将选择下级医院,数量为:
$$ n_b= D(t)P\left(w \leq \frac{e^a[p_h-\theta_h S_h(t)]-p_b+\theta_b S_b(t)}{e^a-1} \right) = D(t)\frac{e^a[p_h-\theta_h S_h(t)]-p_b+\theta_b S_b(t)}{W(e^a-1)} \quad (31) $$
3) 患者选择上级医院的情况。
在这种情况下,患者的效用函数应满足 $ U_h > U_b $,即:
$$ \ln[w-p_h+ \theta_h sh(t)]+ r.(t)+ F_h(t)> \ln[w-p_b+ \theta_b S_b(t)]+ r.(t)+ F_b(t) \quad (32) $$
$$ \Rightarrow \ln\left[\frac{w-p_b+ \theta_b S_b(t)}{w-p_h+ \theta_h S_h(t)}\right]< F_h(t)-F_b(t) \quad (33) $$
选择上级医院的患者数量为:
$$ n_b= D(t)P\left(w> \frac{e^a[p_h-\theta_h
b S_b(t)}{e^a-1} \right) \quad (34) $$
由方程(31)可知,对 $ S_b $ 的投资导致 $ n_b $ 增加,而对 $ S_h $ 的投资导致 $ n_b $ 减少,这说明提高下级医院的医疗保险报销会增加其患者就诊数量,但提高上级医院的报销则会减少下级医院的患者就诊数量。从方程(34)也可得出相同结论,因此医疗保险报销是影响患者选择的重要因素。
接下来,我们将进一步讨论 $ \delta $ 如何影响 $ n_b $ 和 $ n_h $。
推论1 . 下级医院的患者数量将随着患者参考价格效应的增强而增加。
证明 :由方程(31)可知:
$$ n_b= D(t)P\left(\frac{e^a[p_h -\theta_h S_h(t)]-p_b+ \theta_b S_b(t)}{W(e^a -1)} \right) $$
令:
$$ Z= \frac{e^a[p_h -\theta_h S_h(t)]-p_b+ \theta_b S_b(t)}{W(e^a -1)} $$
对 $ n_b $ 关于 $ \delta $ 求一阶导数。
$$ \frac{\partial n_b}{\partial \delta} = \frac{\partial D(t)}{\partial \delta} Z+ D(t) \frac{\partial Z}{\partial \delta} \quad (35) $$
根据方程(3):
$$ \frac{\partial D}{\partial \delta} = r-p+ \theta_b \frac{\partial S_b}{\partial \delta} + \theta_h \frac{\partial S_h}{\partial \delta} \quad (36) $$
对 $ z $ 关于 $ \delta $ 求一阶导数:
$$ \frac{\partial Z}{\partial \delta}=\left(-e^a \frac{\partial S_h}{\partial \delta}+ \frac{\partial S_b}{\partial \delta}\right)/W(e^a -1) \quad (37) $$
将(36)和(37)代入(35),得到:
$$ \frac{\partial n_b}{\partial \delta}=\left(r-p+ \theta_b \frac{\partial S_b}{\partial \delta}+ \theta_h \frac{\partial S_h}{\partial \delta}\right)\frac{e^a[p_h-\theta_h S_h(t)-p_b+\theta_b S_b(t)]}{W(e^a-1)} +\left(\alpha -\beta p(t)+ \delta(r(t)-p(t)+ \theta_h S_h(t))+\theta_b S_b(t)\right)\left[\left(-e^a \theta_h\frac{\partial S_h}{\partial \delta}+ \theta_b\frac{\partial S_b}{\partial \delta}\right)/W(e^a -1)\right] \quad (38) $$
为了确定最优值,求得二阶导数:
$$ \frac{\partial^2 n_b}{\partial \delta^2} = \frac{2 r(r-p)\eta_h\eta_b+ \theta_h^2\rho_h\eta_b+ \theta_b^2\rho_b\eta_h }{W(e^a -1)\eta_h^2\eta_b^2\gamma^2} \quad (39) $$
从第三部分的假设可以看出,上级医院的服务价格、参考价格效应、成本和边际收益均高于下级医院,即 $ \eta_b\theta_b\rho_b< \eta_h\theta_h\rho_h $,由于 $ 0< a< 1 $,可得 $ e^a> 1 $,因此 $ \eta_b\theta_b\rho_b -e^a\eta_h\theta_h\rho_h< 0 $。作为一个凸函数,其最大值可在 $ \frac{\partial n_b}{\partial \delta}= 0 $ 处取得。
根据第四部分的命题,我们在三种不同的博弈论策略下求解方程(38)。随后可分别得到三种不同策略下对应 $ n_b $ 的最大值的最优 $ \delta $:
$$ \delta_{ns}^0= \frac{\eta_h\eta_b(e^a p_h+ p_b)+ \eta_h\theta_h\rho_h+ e^a\eta_b\theta_b\rho_b\gamma}{\lambda_h\rho_h+ \lambda_b\rho_b} \quad (40) $$
$$ \delta_{ss}^0= \frac{\eta_h\eta_b(e^a p_h+ p_b)+(1-\phi)\eta_h\theta_h\rho_h+ e^a\eta_b\theta_b\rho_b(\gamma+ \phi)}{\lambda_h\rho_h+ \lambda_b\rho_b} \quad (41) $$
$$ \delta_{sc}^0= \frac{\eta_h\eta_b(e^a p_h+ p_b)+(1-\phi)\eta_h\theta_h(\rho_h+ \rho_b)+ e^a\eta_b\theta_b(\rho_h+ \rho_b)(\gamma+ \phi)}{\lambda_h\lambda_b(\rho_h+ \rho_b)} \quad (42) $$
由于 $ 0< \delta< 1 $,$ p_h> \rho_h $,$ p_b> \rho_b $,$ \eta_h \geq 1 $,$ \eta_b \geq 1 $ 和 $ \gamma $,$ \phi $,$ \theta $ 均在0到1之间,我们得到 $ \delta_0> 1 $。可以看出,在[0,1]区间内,$ \eta_b $ 的值随着 $ \delta $ 的增加而增加,并在 $ \delta= 1 $ 处取得最大值。
因此,随着患者的参考价格效应增强,患者选择下级医院进行治疗的患者效用得到提升,从而使更多患者在下级医院接受治疗。同样,前往上级医院就诊的患者数量减少,缓解了上级医院的压力。因此,参考价格效应增强了医疗保险报销的杠杆作用,有效提升了患者效用。此外,参考价格效应能够引导患者选择合适的医疗机构,减轻上级医院的压力,同时实现医疗供应链网络的协调。
5.2. 医疗系统的效用
根据方程(6)–(8)可得到不同策略下医疗供应链网络系统的利润,但对于整个医疗系统而言,我们不仅期望供应链的最高利润。作为社会服务机构,医疗系统为人们的生命与健康提供保障,而不是盈利机构。其真正目的在于实现社会的整体效益最优。
由于该供应链仅针对某种常见疾病,如果 $ D(t)> \alpha $ 表示为此疾病提供的医疗资源超过所需,从而导致医疗资源过剩。基于中国医疗资源缺乏的现状下,当医疗资源闲置时,意味着有更多的资源可以用于服务其他类型的疾病,这通常是对疑难重症医疗资源的补充,从而增加利益。
此时,在计算供应链利润时,医院的闲置资源被计入总收入,医疗供应链网络系统的总效用利益函数如下:
$$ W= \begin{cases} \tau\pi_{sc}+ U & D< a \ \tau(\pi_{sc}+(D-n)p)+ U & D> a \end{cases} \quad (43) $$
其中 $ \tau $ 是利润转换为供应链效用的系数[33]。$ \tau> 0 $ 这意味着,供应链利润越高,我们获得的医疗服务效用也越高。
6. 数值分析
采用中国某一地区的数据,分析参考价格对医疗保险报销策略的影响,以及其如何影响患者选择和医疗供应链网络的效用。我们采用了三种不同的博弈论方法,即纳什均衡和斯塔克尔伯格的分散决策方法,以及集中决策方法。
根据调查区域的情况,模型参数的具体取值设定为 $ r_h= 135 $,$ r_b= 90 $,$ p_h= 150 $,$ p_b= 100 $,$ \gamma= 0.3 $,$ W= 1350 $,$ a= 0.5 $,$ \theta_h= 0.6 $,$ \theta_b= 0.5 $,$ \alpha= 300 $,$ \beta= 1 $,$ \eta_h= 1.25 $,$ \eta_b= 1 $,$ \varphi= 0.3 $,$ \tau= 0.8 $,$ \rho_h= 128 $,$ \rho_b= 80 $。
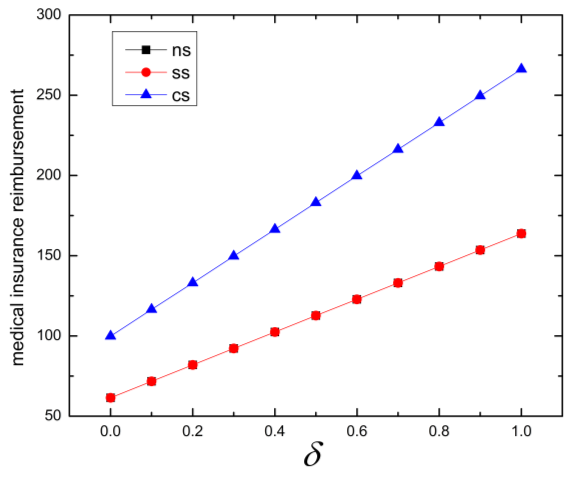
然后可根据公式(27)计算下级医院的补贴率 $ \phi= 0.2 $。首先,我们计算在不同参考价格效应下上级医院和下级医院的医疗保险报销,如表4所示,变化趋势见图2中的4和图2。
| $ \delta $ | $ S_{ns}^h $ | $ S_{ns}^b $ | $ S_{ss}^h $ | $ S_{ss}^b $ | $ S_{cs}^h $ | $ S_{cs}^b $ |
|---|---|---|---|---|---|---|
| 0.00 | 61.44 | 40.00 | 61.44 | 50.00 | 99.84 | 104.00 |
| 0.10 | 71.68 | 46.67 | 71.68 | 58.33 | 116.48 | 121.33 |
| 0.20 | 81.92 | 53.33 | 81.92 | 66.67 | 133.12 | 138.67 |
| 0.30 | 92.16 | 60.00 | 92.16 | 75.00 | 149.76 | 156.00 |
| 0.40 | 102.40 | 66.67 | 102.40 | 83.33 | 166.40 | 173.33 |
| 0.50 | 112.64 | 73.33 | 112.64 | 91.67 | 183.04 | 190.67 |
| 0.60 | 122.88 | 80.00 | 122.88 | 100.00 | 199.68 | 208.00 |
| 0.70 | 133.12 | 86.67 | 133.12 | 108.33 | 216.32 | 225.33 |
| 0.80 | 143.36 | 93.33 | 143.36 | 116.67 | 232.96 | 242.67 |
| 0.90 | 153.60 | 100.00 | 153.60 | 125.00 | 249.60 | 260.00 |
| 1.00 | 163.84 | 106.67 | 163.84 | 133.33 | 266.24 | 277.33 |

从图2可以看出,随着参考价格效应的增加,医疗保险报销也随之增加。患者的心理需求和参考价格效应成为影响医疗决策的主要因素。此外,从表4中可以明显得出,无论是下级医院还是上级医院,集中决策获得的医疗保险报销均高于分散决策。
其次,我们计算了在不同参考价格效应下上级和下级医院的患者就诊人数,如表5所示,其变化趋势见图3。从图3可以看出,随着 $ \delta $ 的增加,就诊患者总数呈上升趋势。同时,上级医院的患者人数减少,而下级医院的患者人数增加,这表明在参考价格效应和医疗保险策略的影响下,患者的就医行为趋于更加合理,从而提高了前往下级医院就诊的患者数量,减轻了上级医院的压力。在所有医疗保险策略中,集中策略在此方面表现最佳,如表5所示。此外,医疗资源得到更合理的利用,使更多患者能够进入医疗系统,并以可接受的价格获得治疗。
| $ \delta $ | $ n_{ns}^b $ | $ n_{ns}^h $ | $ D_{ns} $ | $ n_{ss}^b $ | $ n_{ss}^h $ | $ D_{ss} $ | $ n_{cs}^b $ | $ n_{cs}^h $ | $ D_{cs} $ |
|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 64 | 142 | 206 | 68 | 143 | 211 | 119 | 142 | 261 |
| 0.10 | 72 | 141 | 214 | 77 | 142 | 220 | 141 | 137 | 279 |
| 0.20 | 81 | 141 | 222 | 87 | 141 | 229 | 165 | 130 | 296 |
| 0.30 | 90 | 140 | 230 | 97 | 140 | 238 | 191 | 122 | 313 |
| 0.40 | 100 | 138 | 238 | 108 | 138 | 247 | 218 | 111 | 330 |
| 0.50 | 110 | 136 | 246 | 119 | 136 | 255 | 247 | 99 | 347 |
| 0.60 | 120 | 134 | 254 | 131 | 133 | 264 | 278 | 86 | 364 |
| 0.70 | 131 | 131 | 262 | 143 | 129 | 273 | 311 | 70 | 381 |
| 0.80 | 142 | 127 | 270 | 156 | 125 | 282 | 345 | 53 | 399 |
| 0.90 | 154 | 124 | 278 | 169 | 121 | 291 | 381 | 34 | 416 |
| 1.00 | 166 | 120 | 286 | 183 | 116 | 299 | 419 | 13 | 433 |
 纳什策略(NS);(b) 斯塔克尔伯格策略(SS); (c) 集中式策略(CS)。)
纳什策略(NS);(b) 斯塔克尔伯格策略(SS); (c) 集中式策略(CS)。)
最后,我们计算不同策略下供应链的总利润,结果如表6所示,其趋势可在图4中看到。
| $ \delta $ | $ \pi_{ns} $ | $ \pi_{ss} $ | $ \pi_{cs} $ |
|---|---|---|---|
| 0.00 | 22,760.82 | 23,128.96 | 25,552.43 |
| 0.10 | 23,163.00 | 23,563.60 | 25,885.91 |
| 0.20 | 23,510.40 | 23,935.21 | 26,012.04 |
| 0.30 | 23,803.02 | 24,243.78 | 25,930.83 |
| 0.40 | 24,040.86 | 24,489.32 | 25,642.28 |
| 0.50 | 24,223.92 | 24,671.83 | 25,146.39 |
| 0.60 | 24,352.21 | 24,791.31 | 24,443.16 |
| 0.70 | 24,425.72 | 24,847.75 | 23,532.59 |
| 0.80 | 24,444.44 | 24,841.16 | 22,414.68 |
| 0.90 | 24,408.39 | 24,771.54 | 21,089.42 |
| 1.00 | 24,317.57 | 24,638.88 | 19,556.83 |
当 $ D(t)< \alpha $ 时,医疗资源供不应求,所有策略下的总收入随着参考价格效应的增强而增加。因此,医疗保险投资不仅提高了患者就医意愿,还增加了医疗机构的利润,实现了双赢局面。当 $ D(t)> \alpha $ 时,意味着医疗资源闲置。在CS策略下,该疾病的总利润减少,但总医疗成本会下降,从而解决了医疗保险投资持续增加但患者总医疗成本也上升的问题。从整体医疗系统来看,常见疾病基本可在下级医院治愈,这是对资源的合理利用。上级医院的医疗资源可用于治疗相对复杂的疾病,从而提升医疗系统的整体效用。医疗供应链网络在不同决策下的总效用如表7所示。
| $ \delta $ | $ W_{ns} $ | $ W_{ss} $ | $ W_{cs} $ |
|---|---|---|---|
| 0.00 | 32,902.73 | 33,221.73 | 36,808.27 |
| 0.10 | 33,461.44 | 33,817.85 | 37,706.09 |
| 0.20 | 33,985.93 | 34,375.26 | 38,480.61 |
| 0.30 | 34,476.20 | 34,893.95 | 39,131.82 |
| 0.40 | 34,932.27 | 35,373.93 | 39,659.73 |
| 0.50 | 35,354.11 | 35,815.20 | 40,064.34 |
| 0.60 | 35,741.75 | 36,217.75 | 40,345.65 |
| 0.70 | 36,095.17 | 36,581.58 | 40,503.66 |
| 0.80 | 36,414.37 | 36,906.70 | 40,538.36 |
| 0.90 | 36,699.36 | 37,193.11 | 40,579.76 |
| 1.00 | 36,950.14 | 37,440.80 | 40,618.86 |
整个医疗系统的患者总数和社会效益显著大于分散决策情况下的结果。换句话说,通过医疗供应链网络的垂直整合协调,可以最大化整体利益。
7. 结论与未来研究
7.1. 结论
本文建立了一个具有参考价格效应的动态博弈论模型,并分析了医疗保险报销策略对医疗供应链网络协调的影响。结果表明:
1) 医疗保险报销策略与患者的参考价格效应呈正相关。较高的参考价格效应可以获得更多的报销,而边际利润和服务效率等其他因素也会影响报销。政府应充分考虑这些因素,并利用保险报销作为有效工具,推动医院提高服务质量、降低成本并控制卫生支出的增长。
2) 利用医疗保险中的参考价格效应可以引导患者选择。患者会根据不同医疗保险报销策略做出理性选择。医院获得不同的医疗保险报销,并以此提升服务质量并优化医疗资源。在新医改政策下,政府提高了医疗保险报销水平,从而增强患者的参考价格效应。随着患者参考价格效应的增强,患者选择下级医院治疗的效用得到提升,因此更多患者会在下级医院接受治疗。同样,前往上级医院就诊的患者数量减少,有助于缓解患者拥挤问题。通过这种方式,医疗保险能够引导患者选择。这不仅减轻了上级医院患者拥挤的压力,也促进了下级医院就诊患者数量的增加。此外,利用参考价格效应可提高医疗资源的有效利用,使更多患者能够以可接受的价格进入医疗系统接受治疗。
3) 参考价格效应能够在所有不同的医疗保险策略下提高医疗供应链网络的效用。此外,与纳什均衡和斯塔克尔伯格博弈的分散决策相比,集中决策能够加强不同医疗机构之间的合作意愿,降低医疗总费用,并提高整个医疗供应链网络的效用。至于由此可以看出,数值分析:1)在表4的集中决策部分下,上级和下级医院在集中决策下的报销均高于NS和SS的分散决策。额外的报销将提高上下级医院之间的合作意愿。2)在表5中,集中决策部分表明,当下级医院的患者收治数量增加时,上级医院的收治率下降。在所有医疗保险策略中,集中策略在此方面表现最佳。此外,下级医院的平均价格低于上级医院,但报销更高,这将降低患者的医疗费用。3)从表7也可以看出,医疗供应链网络在集中决策下的总效用高于分散决策。综上所述,集中决策情景能够进一步促进医疗资源更高效地分配。通过更战略性的医疗资源分配,医疗服务将对患者更加可及且价格更加可负担,因此医疗供应链网络的垂直整合结合集中决策为医疗供应链网络提供了最佳结果。
7.2. 启示与局限性
为确保医疗供应链网络的可持续发展,政府在制定医疗保险报销策略时,应充分考虑参考价格效应,并发挥其杠杆作用,以使医疗保险基金投资获得最大的经济效益。医疗保险报销可用于优化医疗资源的分配。下级医院应获得更多的报销,以提升其服务质量,从而使患者更倾向于选择下级医院,降低医疗费用,并提高患者满意度。在医疗供应链网络管理中,政府应发挥主导作用,通过集中决策来平衡各方利益。总之,通过实施集中决策下的垂直整合供应链,可实现医疗资源的合理利用,提升医疗服务质量,降低医疗支出,推动医疗供应链网络的可持续发展。
本文的一个局限性是研究仅考虑了常见疾病,未包括严重或危及生命的疾病或急诊情况。此外,研究数据来自一个地理区域,该区域可能具有其特有的经济状况。因此,我们可以通过对严重疾病进行比较研究,并在不同情境下测试模型,来扩展研究范围。
7.3. 未来研究建议
在未来的研究中,或许可以进一步探讨以下几个方面:(i)可进一步研究影响患者心理参考价格的因素,例如患者特征及其医学知识。(ii)优化医疗保险,针对不同的医疗服务(包括手术治疗、护理检查和设备)以及不同疾病采用不同的医疗保险报销比例,以提高医疗保险效用。




















 53
53

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








