数据结构之二叉平衡树

二叉平衡树（AVL树），是带有平衡条件的二叉树查找树，这个平衡条件必须要容易保持，且必须保证树的深度是O(logN).。这里的平衡条件是左右子树高度差最多差1的二叉查找树。如果插入一个节点后破坏了平衡条件，那么就要做一些操作去恢复AVL树， 这里的操作一般称为旋转。

第一种情况是插入的节点在外面，即（左-左或右-右）、另一种是节点插在里面，即（左-右或右-左）， 对于第一种情况我们采用单旋转，第二种采用双旋转，如下图：

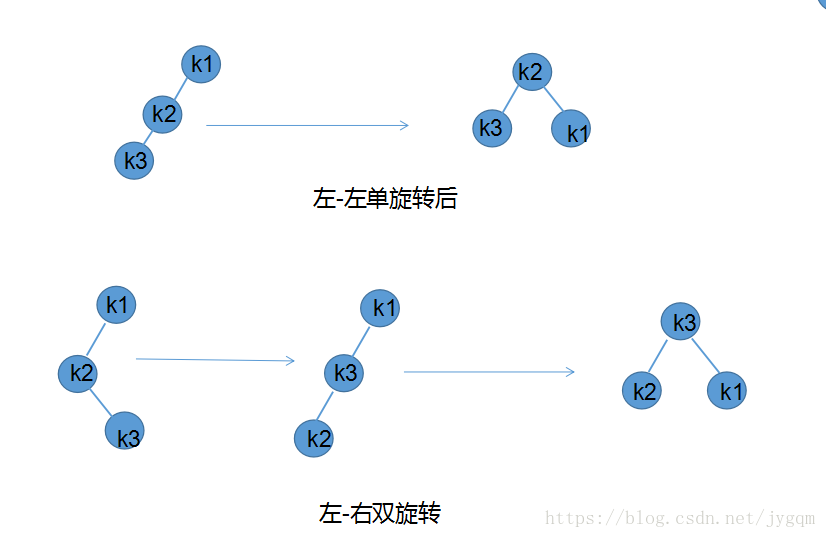
代码实现

头文件 avl.h

#ifndef AVL_H_
#define AVL_H_

struct Node;
typedef int ElementType;
typedef struct Node *ptrToNode;
typedef struct Node *AVLTree;

// 插入节点
ptrToNode insert(AVLTree T,ElementType e);
// 左单旋转
ptrToNode singleRoateWithLeft(ptrToNode ptr);
// 左右双旋转
ptrToNode doubleRoateWithLeftRight(ptrToNode ptr);
// 右单旋转
ptrToNode singleRoateWithRight(ptrToNode ptr);
// 右左双旋转
ptrToNode doubleRoateWithRightLeft(ptrToNode ptr);
// 中序遍历
void midPrint(AVLTree T);
// 返回节点的高度
int height(AVLTree T);
// 返回最大值
int max(int a, int b);
// 销毁树
void destory(AVLTree &T);

#endif /* AVL_H_ */

具体实现