梯度上升VS梯度下降，加还是减

梯度下降VS梯度上升

梯度下降是一种常用的优化算法，公式是这样的：

$$w^{(\tau+1)} = w^{\tau} - \alpha \nabla E(w^{\tau})$$

其中， $\nabla E(w)$ 是cost函数的梯度，减去这个值和学习率的乘积，就代表沿着最陡峭的面滑向最低点。嗯，没有问题。

可是有一天看到有本书提到梯度上升，公式是这样的：

$$w = w + \alpha \nabla_{w} f(w)$$

嗯，也容易理解，式1中 $E(w)$ 是个碗的形状，要下降到最低点，式2中 $f(w)$ 是个蘑菇的形状，要上升到最顶点。$E(w)$ 加个负号就变成 $f(w)$ 了。

等等，这一对比才意识到还有一个问题：为什么下降就一定是减，上升就一定是加？

梯度、导数、倾斜方向

要回答这个问题，就要理解梯度的含义，梯度是三维以上坐标系的概念，它在平面坐标系对应的概念是导数。

那么我们先来看导数，它表示线的斜率，斜率又可以分两部分来看，一个是倾斜的程度（我有多斜），一个是倾斜的方向（我往那儿斜）。此处只讨论倾斜方向。

其实二维平面上只两个倾斜方向：往左斜和往右斜。有人就怀疑了，为什么没有往上斜和往下斜，因为那是根线啊，这两种说法一样，我们取其一种说法而已。又有人怀疑了，你说它上头往左斜，它同时下头就往右斜啊。也对，那为了把事儿说清楚，我们就只看一、二象限。总而言之，倾斜方向只有两个，为了表述清楚，我们需要加一些限制。二维平面的倾斜方向正好对应导数的正负，导数为正，线右倾，导数为负，线左倾。

二维平面中， 导数 代表 线 的倾斜方向和倾斜程度，三维空间中， 梯度 代表 面 的倾斜方向和倾斜程度。线的倾斜方向只有两个用正负表示，而面的倾斜方向是无穷的，是由向量表示。

梯度是个向量，向量的方向就代表倾斜方向，向量的模就代表倾斜程度。图1绘制了三维空间中两个倾斜的平面和一个参考水平面，为了清晰，画出了两个视角的截图：

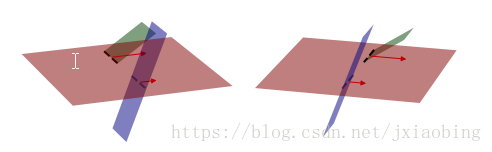
如图所示，三维空间中面的梯度是二维向量，我把它画在Z=0的XY平面上，它就是这个倾斜平面的梯度向量，它垂直于这个平面与水平面的交线，图中画的两个面倾斜方向是一样的，倾斜程度不同，也就是梯度向量方向相等，模不相等。这里就可以看到面的倾斜方向的含义，同样的，为了表述明确，需要几个限制，一是倾斜是以面的锐角夹角方向，二是从右手坐标系上方视角来看的。

加梯度永远是向上的

现在很明显了，加梯度，就是自变量沿着面的倾斜方向移动，函数值就会向上移动。对于平面如此，而到了曲面上，某个点的梯度就是该点切面的倾斜方向和倾斜程度。所以对碗形函数求极小值，就要减梯度，对蘑菇形函数求极大值，就要加梯度。