混合交通流中自动驾驶与人工驾驶的跟驰模型分析

基于跟驰模型的有人驾驶与自动驾驶汽车混合交通流分析

1. 引言

自动驾驶汽车几十年来一直是一个热门话题，未来也将持续受到关注。事实上，在城市中，人工驾驶汽车和自动驾驶汽车将同时存在。这两种类型的汽车将如何协同运行？对混合交通流进行建模是解决这一问题的通用工具。作为微观交通流模型之一的跟驰模型已经发展了数十年，被广泛用于描述系统中单个车辆的行驶行为。1953年，Pipes[1]首次提出了经典的跟驰模型来描述一串车辆的行为。此后，大量改进的跟驰模型被提出，以更加真实地描述交通动态。Bando等[2]通过用最优速度函数替代前车速度改进了Pipes的跟驰模型，克服了经典模型的不足。Holland[3]提出了一种通用判据，用于判断是否会引发灾难性事件。该判据与系统的稳定性条件相一致跟驰模型。长谷川[4]和泽田[5]通过考虑次近邻相互作用改进了最优速度模型，显著增强了交通流的稳定化，并获得了mKdV方程的解。江等人[6]基于改进的最优速度模型建立了全速度差模型，当前车辆与前车之间的相对速度对交通稳定性具有显著影响。伦茨等人[7]和中山等人[8, 9] 在协同驾驶系统中引入前向和后向效应，扩展了最优速度模型，从而增强了均匀流的稳定性。张等人[10]提出了一种新的跟驰模型以描述多相交通，成功再现了所谓的通行能力下降和交通滞后环现象。葛等人[11]和李等人[12]在智能交通系统环境下，采用非线性方法分析了扩展最优速度模型。余等人[13]研究了扩展最优速度模型的扭结‐反扭结特性。彭[14]基于跟驰理论，提出了考虑预期驾驶行为个体差异的新格子模型。余等人 [15]在改进最优速度模型时，不仅考虑了全速度差，还引入了加速度差。吴国锐 [16]通过解析方法研究了交通流的不稳定性，指出智能车辆的应用是消除交通流不稳定性的潜在解决方案，并利用线性分析方法确定了异质交通流的稳定性阈值。唐等人[17, 18]通过考虑车际通信及其可靠性，提出了新的扩展版跟驰模型。张等人[19]采用扩展的宏观动力波交通流模型研究混合交通流，考虑了两种类型车辆（客车和卡车），且假设它们具有相同的自由流速度，该模型可用于研究长距离拥堵高速公路。葛等人[20]提出了基于加速度的联网巡航控制，以提高道路通行能力。这种基于加速度的联网巡航控制设计为可通过无线车对车（V2V）通信接收前方多辆车的加速度信号，从而提供鲁棒性能，并保持对大规模联网车辆系统的可扩展性。葛等人[21]和雷德胡等人[22]分别应用延迟反馈控制方案来改善交通流行为，这些方法已被证明在抑制交通拥堵方面有效。余和石[23-25]提出了两种新的联网巡航控制策略，分别考虑了多个前车速度变化的记忆效应以及车距波动，以提升道路通行能力、增强交通安全并减少燃油消耗和尾气排放。他们通过数值模拟验证了模型的有效性。Work et al[26]研究了有人驾驶与自动驾驶混合车辆的交通流。基于已有模型，构建了一个二阶连续交通流模型来描述混合交通流。数值结果验证了该模型的有效性。Tang et al[27-28]提出了一个扩展的宏观交通流模型，考虑了驾驶员有限理性和信号交叉口处的速度引导模型，考虑了驾驶员有限理性。驾驶员有限理性在影响交通流行为方面起着重要作用。此外，Tang et al[29-30]研究了在平衡状态下不迟到时能耗和排放对行程成本的影响，并提出了一个扩展的跟驰模型，以研究驾驶员有限理性对其微观驾驶行为和燃油消耗的影响。最近，Tang et al[31]提出了一个跟驰模型，用于研究信号灯对车辆通过交叉口全过程中的驾驶行为、燃油消耗和排放的影响。这些研究很有意义。上述文献主要讨论了一些与协同驾驶、智能交通系统和控制机制相关的跟驰模型。但涉及有人驾驶汽车与自动驾驶汽车混合交通流的研究较少。本文将采用跟驰模型研究混合交通流的基本图和密度波。

本文其余部分组织如下。在第2节中，给出了人工驾驶汽车和自动驾驶汽车的动力学模型，并依次给出了一条引理和一个定理。在第3节中，针对三种情况进行了数值模拟，一些新结果通过图展示。在第4节中，给出了总结。

2. 模型

假设在周期性边界条件下，一股混合了人工驾驶汽车和自动驾驶汽车的交通流在单车道公路上行驶，且不允许超车。 给出了示意图，N辆车均匀分布在道路上（有人驾驶汽车为蓝色，自动驾驶汽车为橙色）。在周期性边界条件下，第Nth 辆车是前导车，而第(N+1) th 辆车是第一辆车。毫无疑问，这两类车辆的驾驶模式不同，因此它们的运动方程也不同。下面我们分别讨论人工驾驶汽车和自动驾驶汽车的动力学模型。

2.1 人工驾驶汽车的动力学模型

众所周知，Bando模型适用于描述有人驾驶汽车的行为。其表达式为

$$
\ddot{x}_j(t) = a \times \left[ V(\Delta x_j(t)) - \dot{x}_j(t) \right]
$$

其中a为驾驶员的敏感度，通常a=1/τ且τ为对前车的反应时间，$\dot{x} j(t)$和$\ddot{x}_j(t)$表示第j辆车在时间t的加速度和速度，$\Delta x_j(t) = x {j+1}(t) - x_j(t)$表示第j辆车与第(j+1)辆车之间的车头间距。该函数为第j辆车的最优速度函数（OVF），如参考文献[27]所给出。

$$
V(\Delta x_j(t)) = \frac{v_{\text{max}}}{2} \left[ \tanh(0.13 \Delta x_j(t) - 1.57) + \tanh(0.13 \times 1.57) \right]
$$

$v_{\text{max}}$表示最大速度，并$l_j$表示第j辆车的长度。

将使用线性稳定性理论来分析均匀流的稳态，即在周期性边界条件下所有车辆以恒定车头时距和速度行驶。公式(1)中均匀稳态的解由下式给出

$$
x_{j,0}(t) = hj + V(h)t
$$

其中h为相同车头时距，L为道路总长度，N为系统中的车辆总数。 $h = L/N$

根据经典线性系统稳定性理论，给出如下引理

引理1。 如果满足以下条件

$$
a > 2V’(h)
$$

那么，在采用最优速度模型的交通流中，交通拥堵永远不会发生。否则，将会发生交通拥堵。

2.2 自动驾驶汽车的动力学模型

配备多种传感器的自动驾驶汽车能够检测前后车辆，实时获取前后车头时距。基于Bando模型，本文提出了一种新的自动驾驶汽车流数学模型。

$$
\ddot{x} j(t) = \alpha \times \left[ V_1(\Delta x_j(t), \Delta x {j-1}(t)) - \dot{x}_j(t) \right]
$$

其中$\alpha$是自动驾驶汽车上配备的传感器的敏感度，可根据实际状况进行调节。其他变量与前述相同。$V_1(\Delta x_j(t), \Delta x_{j-1}(t))$是最优速度函数，基于汽车上的前向传感器和后向传感器给出

$$
V_1(\Delta x_j(t), \Delta x_{j-1}(t)) = (1-p)V(\Delta x_j(t)) + pV(\Delta x_{j-1}(t))
$$

其中p为常数，且与公式(2)中的形式相同。 $V(\Delta x_j(t))$和$V(\Delta x_{j-1}(t))$

自动驾驶汽车的敏感度高于人类驾驶的敏感度汽车，因为自动驾驶汽车中的电子传感器比驾驶员更敏感。敏感度$\alpha$始终小于$a$。

新模型的思想是：当前车距大于后车距时，车辆将获得更大的期望速度；当前车距小于后车距时，车辆将获得更小的期望速度；当前车距等于后车距时，车辆将获得期望速度。

从上述思路可知，由于因子p的作用，不仅增强了交通流的稳定性，还提高了安全性。它使得自动驾驶汽车在路上行驶时尽可能均匀。因此，模型中的参数p被称为“平滑因子”。

根据引理1，可以从上述新模型中提出一个定理如下

定理1。 如果满足以下条件

$$
\alpha > \frac{2V’(h)}{1 + 2p}
$$

那么在均匀自动驾驶汽车流中，交通拥堵永远不会发生。否则，将会发生交通拥堵。

证明 假设$\delta x_j(t)$是均匀流的一个微小偏差，那么

$$
x_j(t) = x_{j,0}(t) + \delta x_j(t)
$$

将上述方程代入公式(5)并忽略高阶项后，得到线性化方程，

$$
\delta \ddot{x} j(t) = \alpha \times \left[ V’(h)(1+p)\delta \Delta x_j(t) - p \delta \Delta x {j-1}(t) - \delta \dot{x}_j(t) \right]
$$

进一步地，

$$
\beta_k^2 + i\beta_k s - \alpha V’(h) \left[ (1+p)(e^{i\beta_k} - 1) + p(e^{-i\beta_k} - 1) \right] = 0
$$

公式(10)的解形式为$\beta_k = s_k + i\omega_k$。通过忽略解的高阶项，得到的一阶和二阶项如下

$$
s_1 = V’(h) \quad \text{and} \quad s_2 = \frac{\alpha}{2} \left[ V’‘(h) + (1+2p)V’(h)^2 \right]
$$

如果均匀流是稳定的，则必须满足以下条件

$$
\lim_{t \to \infty} \delta x_j(t) = 0
$$

代入公式(11)后，可以很容易地推导出以下条件

$$
s_2 > 0 \quad \text{i.e.} \quad \alpha > \frac{2V’(h)}{1 + 2p}
$$

因此，定理1成立。

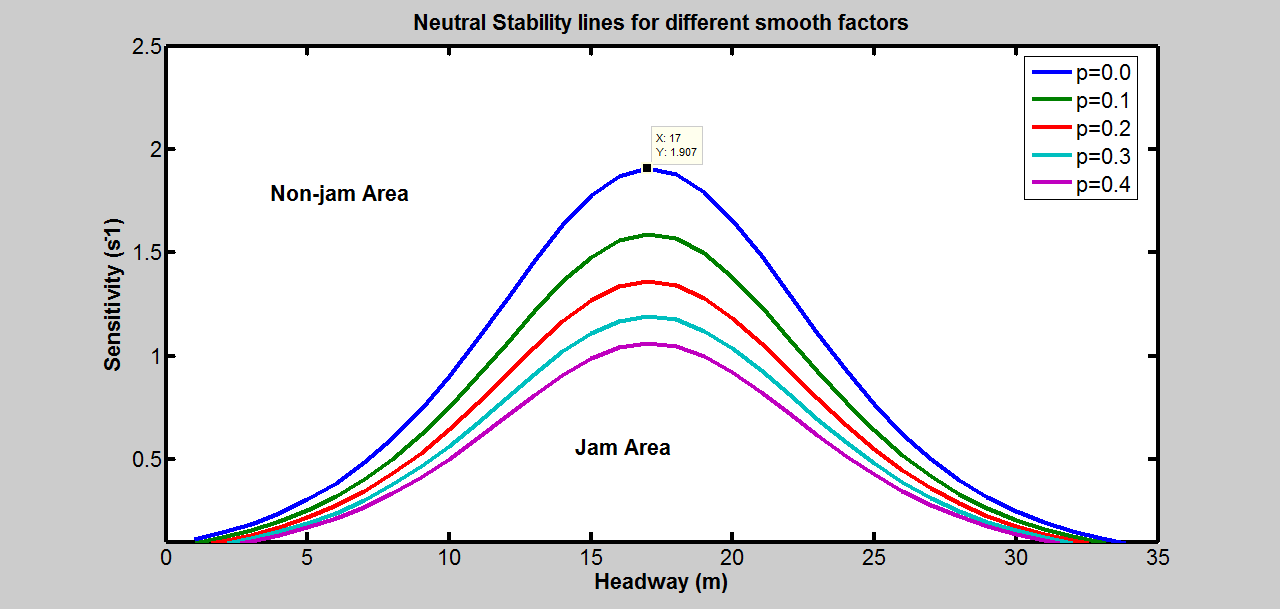
根据上述稳定性条件，让我们来分析平滑因子。中性稳定线已在 中绘制。中性稳定线上方的区域为非拥堵区域，下方的区域为拥堵区域。中性稳定线的顶点处存在一个临界点。当p=0.0时，该临界点为(17, 1.907)，在数据提示中可观察到。从该图中可以得出结论：平滑因子越大，稳定区域也越大。

3. 数值模拟

在一条长度为L米的单车道道路上，有N辆车，在周期性边界条件下不允许超车。车辆序号从0th到(N‐1) th ，第N th辆是该系统中的第一辆车。设$v[j][t]$和$x[j][t]$表示在时间t时第jth辆车的速度和位置。交通流的初始状态为

$$
v[0][0] = v[1][0] = \cdots = v[N-1][0] = 0
$$

$$
x[0][0] = 0, \quad x[j][0] = x[j-1][0] + L/N, \quad j = 1,2,\ldots,N-1
$$

基于牛顿第二运动定律的更新规则

$$
x[j][t + \Delta t] = x[j][t] + v[j][t] \times \Delta t + 0.5 \times a[j][t] \times (\Delta t)^2
$$

$$
v[j][t + \Delta t] = v[j][t] + a[j][t] \times \Delta t
$$

最优速度函数中的参数单位为米/秒。在不失一般性的前提下，假设无论是自动驾驶汽车还是其他车辆，每辆车的长度都被视为相同。仿真时间步长为$\Delta t = 1.0$ s。

仿真1

在仿真1中，让我们检查具有不同敏感度、平滑因子和混合比例的混合交通流的基本图。因此，我们将在三种情况下进行仿真。持续时间为20000个时间步长，这足以使交通流达到稳态。在仿真中，交通流的变化密度可以通过两种方式实现。

首先，道路长度是不变的，而车辆数量以固定的数量增加。方程如下所示，

$$
\rho(n) = \frac{V(n)}{L}, \quad V(n) = V(n-1) + \Delta V, \quad n = 1,2,\ldots,99, \quad V(0) = 1
$$

其中$V(n)$表示第nth次仿真中的车辆数量，$\Delta V$是车辆的固定增加量。

其次，汽车数量不变，道路长度减少一个固定长度。表达式如下所示，

$$
\rho(n) = \frac{N}{L(n)}, \quad L(n) = L(n-1) - \Delta L, \quad n = 1,2,\ldots,99, \quad L(0) = (N-1)\Delta L
$$

其中$L(n)$表示第nth次模拟的道路长度，$\Delta L$是道路的一个固定的减少长度。

交通流的流量采用以下方程。

$$
Q = \rho v
$$

其中，$Q$表示流量，$\rho$表示流密度，$v$是在时间段$\Delta T$内的平均速度

$$
v = \frac{1}{T \Delta} \sum_{t=T+1}^{T+\Delta T} \frac{1}{N} \sum_{i=1}^{N} v_i(t)
$$

其中，$v_i(t)$是第ith辆车在时间t的速度。$\Delta T$是一个时间段。N是车辆总数。

在以下仿真中，数据从 18000th步采集到19000th步，用于计算平均速度和流量。

仿真1.1

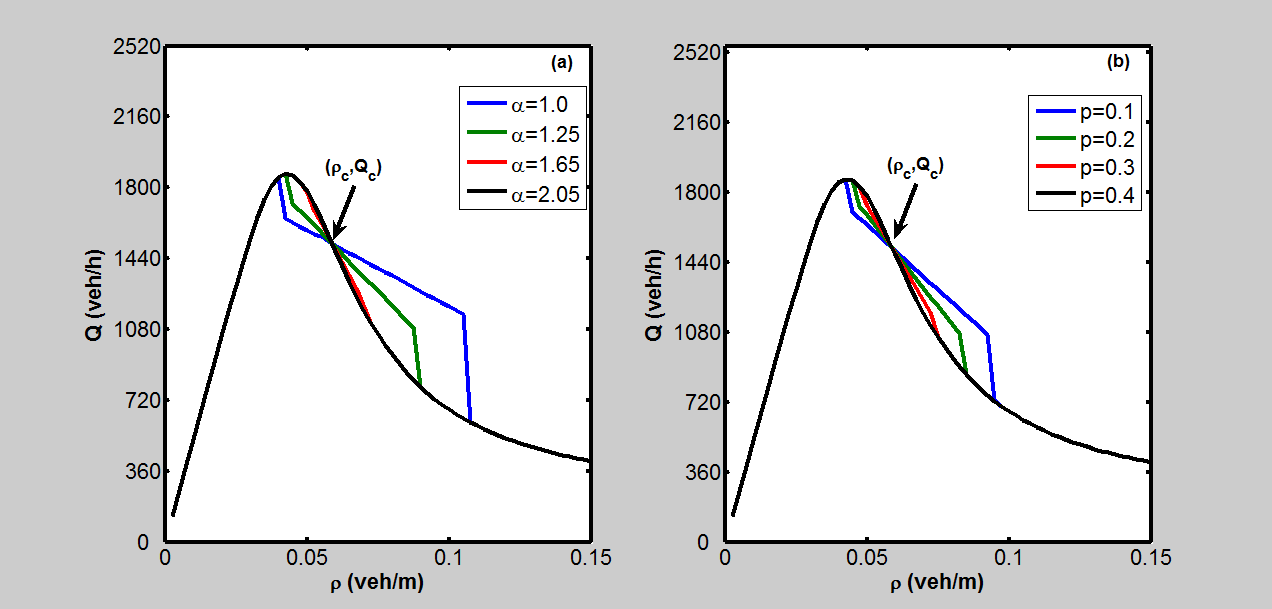
本仿真旨在检验在无任何人工驾驶汽车参与的情况下，敏感度和平滑因子对自动驾驶汽车流的影响。道路长度保持不变。为了实现变化密度，每次向系统中加入一定数量的自动驾驶汽车。考虑到流量与密度的关系，每次向车流中增加4辆自动驾驶汽车，共进行100次。因此，密度值从0.0025至 0.25辆/米变化。仿真在以下两种情况下进行：1）变化的敏感度和平滑因子； 2）变化的平滑因子和敏感度。仿真结果如 所示，其中模式(a)和(b)分别对应于变化的敏感度和平滑因子。从模式(a)可以看出，基本图中存在一个临界点。当密度小于临界密度时，交通流的更大流量对应更高的敏感度；当密度大于临界密度时，交通流的更大流量对应更低的敏感度。从模式(b)可以看出，平滑因子对交通流量具有相同的影响。在临界密度之前，平滑因子越大，交通流量越大；在临界密度之后，交通流量表现出相反的变化趋势。

仿真1.2

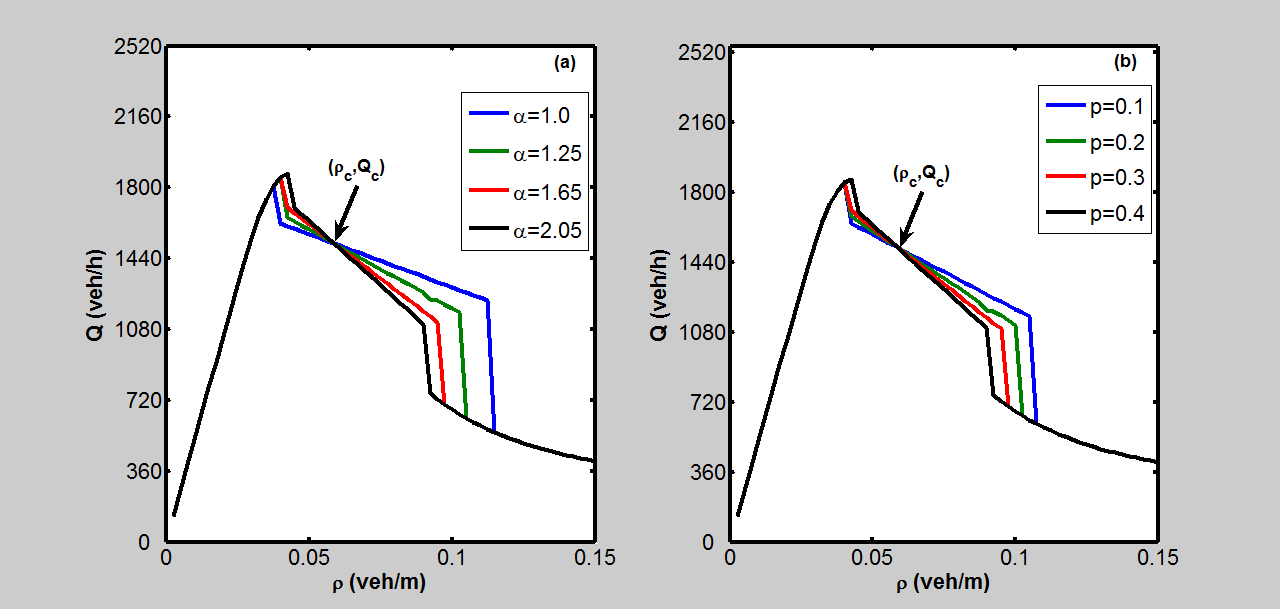
将进行此数值模拟，以检查敏感度和平滑因子对具有混合比例50%的混合交通流的影响。人工驾驶汽车和自动驾驶汽车在道路上依次交替分布。变化密度的获取方式与仿真1.1中相同。每次添加的车辆中包含50%的自动驾驶汽车和50%的人工驾驶汽车。采用与仿真1.1相同的案例，即1）；2）。仿真结果如 所示。从图(a)、(b)中可以得出与仿真1.1相同的结论：在临界密度之前，更高的敏感度和平滑因子能够获得更大的交通流量；而在临界点之后则表现出相反的变化趋势。从仿真1.1和1.2可以看出，图3-2中的变化密度范围明显大于图3-1中的范围。这说明混合交通流的稳定性弱于自动驾驶汽车流。

仿真1.3

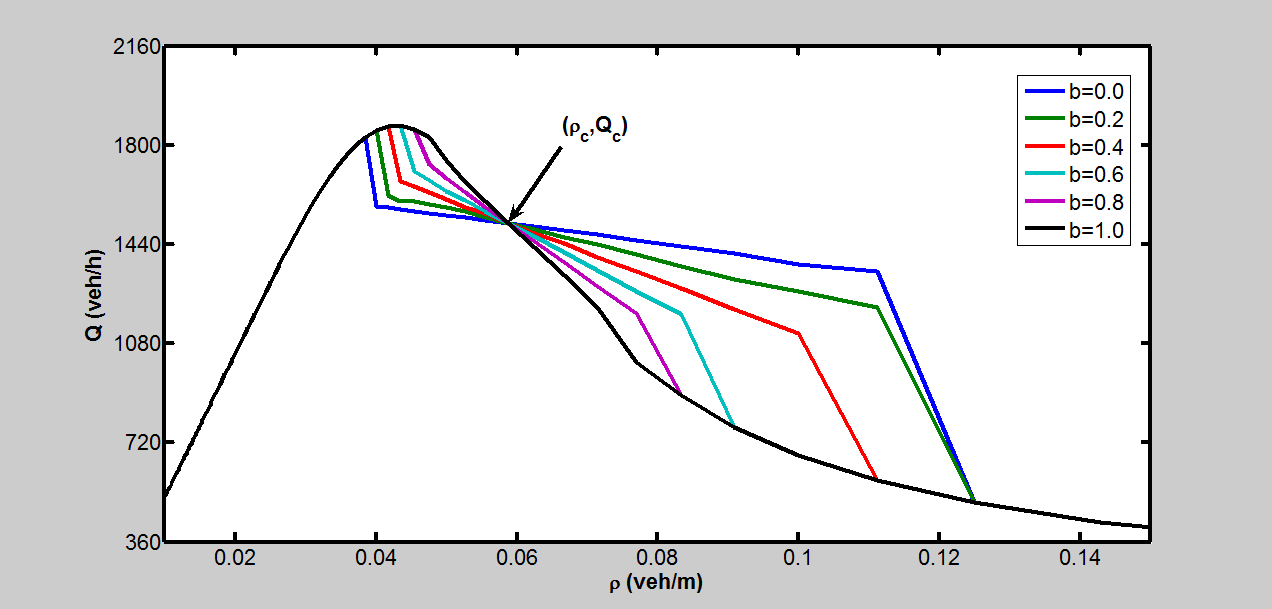
在本仿真中，我们将检验不同混合比例下混合交通流的基本图。不失一般性，假设$b=0.0$表示交通流中没有自动驾驶汽车，$b=1.0$表示交通流中全部为自动驾驶汽车。车辆总量为100，混合比例以0.2为步长从0.0变化到1.0。人工驾驶汽车和自动驾驶汽车的敏感度分别为$a=0.85$和$\alpha=1.0$，平滑因子为$p=0.3$。变化密度可通过以下方式获得：车辆数量保持不变，道路长度每次减少100米，从10000米递减至100米。因此，在仿真中密度从0.01变化到1.0。仿真结果如 所示，模式中也观察到了一个临界点。在临界密度之前，自动驾驶汽车越多，流量越大；相反，在临界密度之后，自动驾驶汽车越少，流量越大。

从仿真1可以得出结论，无论是自动驾驶汽车流还是混合交通流，流量在一定密度范围内都会受到敏感度和平滑因子的影响。在此范围之外，流量对这两个因素不敏感。不同之处在于，混合交通流的变化密度范围比纯自动驾驶汽车流更大。

模拟2

在本部分中，让我们分别检查自动驾驶汽车流在不同敏感度和平滑因子下的稳定性。模拟2的持续时间为200000个时间步长。在该模拟中，道路长度为 1700米，交通流中的自动驾驶汽车数量为100辆。

模拟2.1

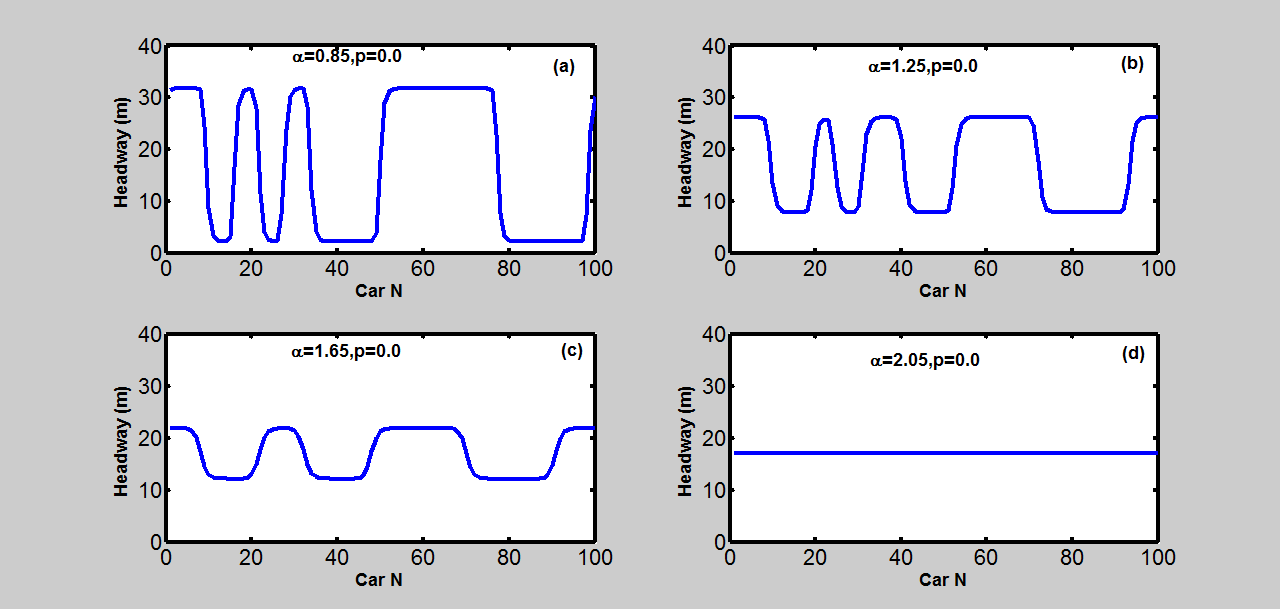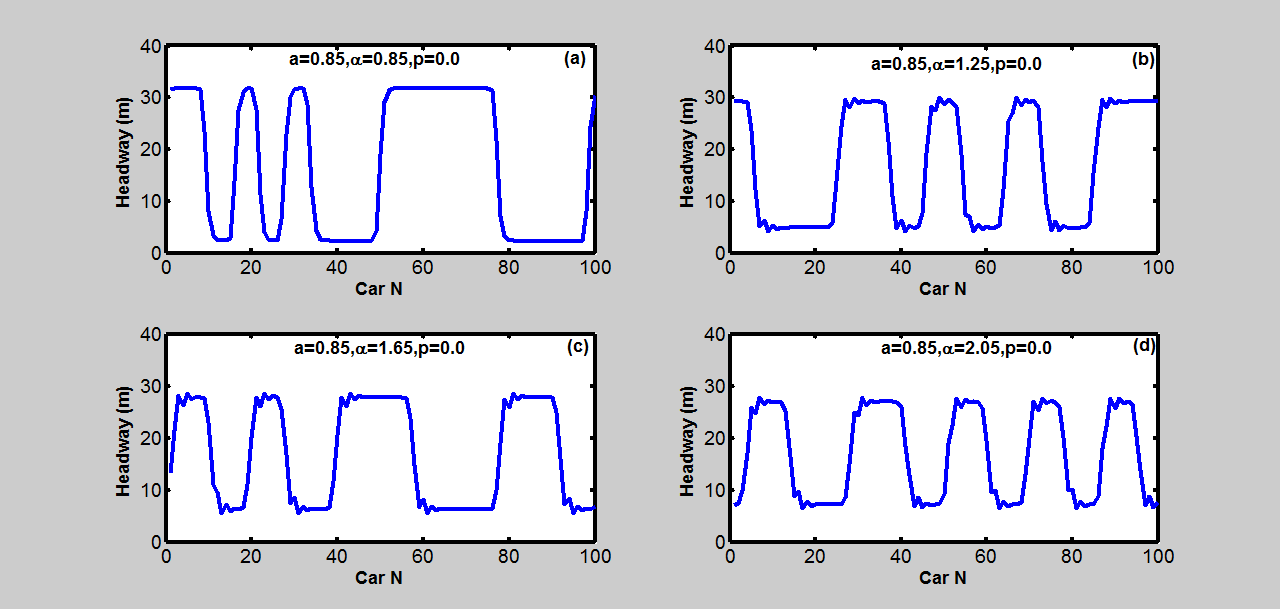
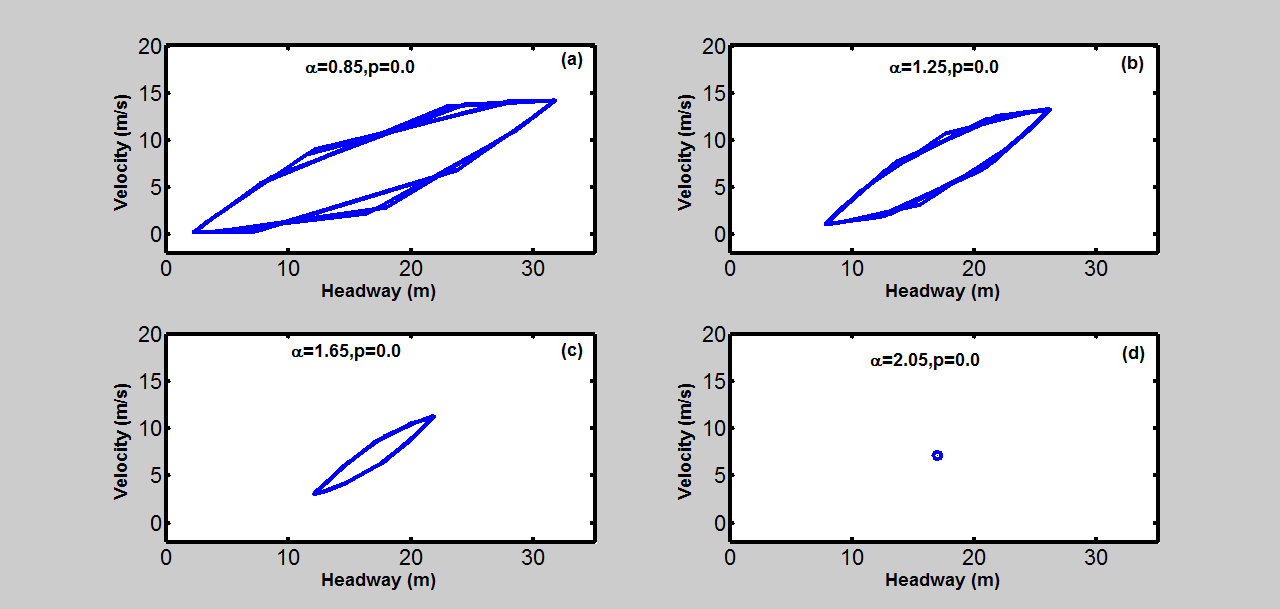
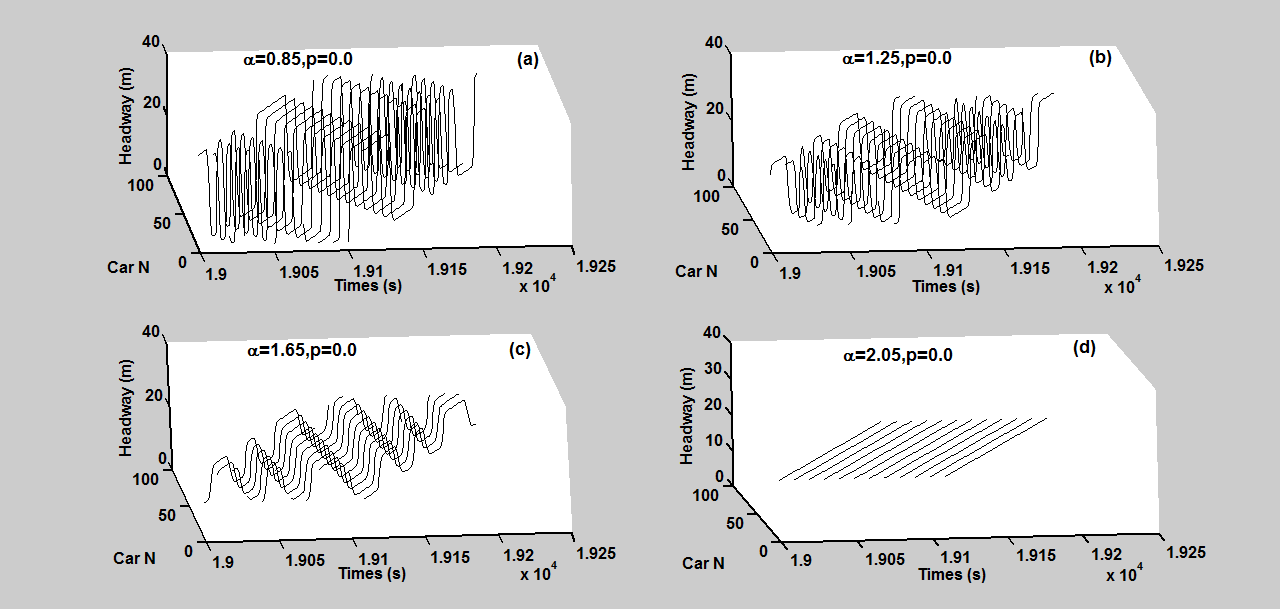
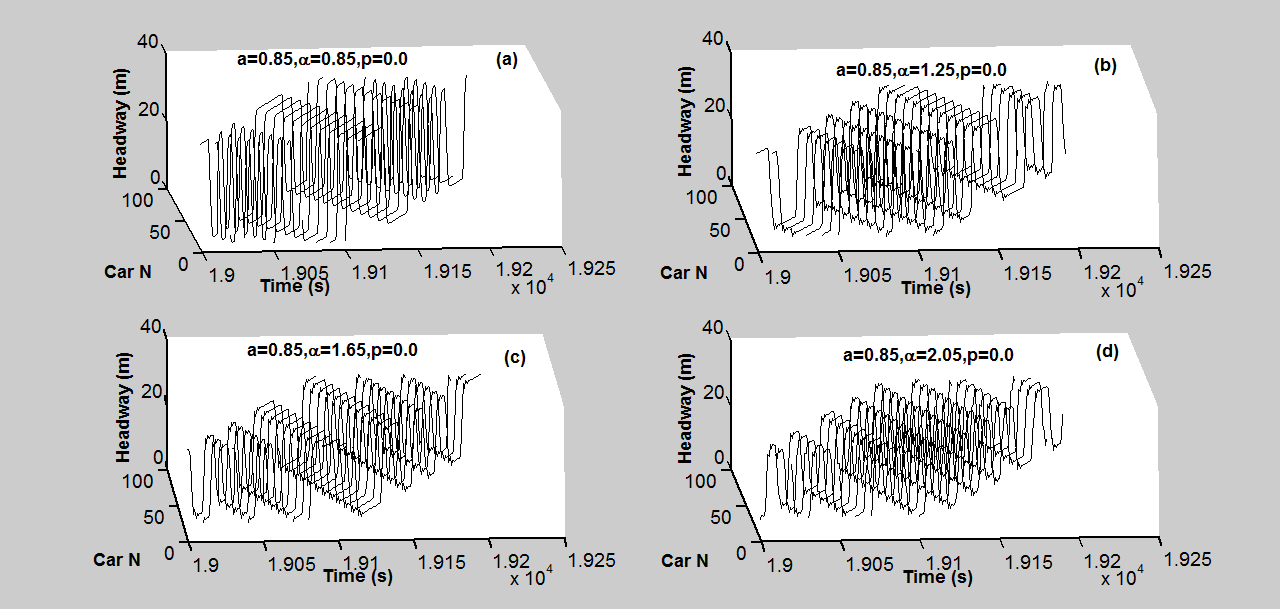
敏感度取为以下值：$\alpha = 0.85, 1.25, 1.65, 2.05$，不考虑平滑因子。仿真结果如 至 所示。这些图中的(a)到(d)模式分别对应于不同敏感度的情况。 中的模式展示了在时间t=19000秒时具有不同敏感度的自动驾驶汽车的车头时距分布。从这些模式可以看出，随着敏感度增大，自动驾驶汽车流的稳定性增强。 中的模式显示了在时间t=19000秒时具有不同敏感度的自动驾驶汽车流的滞回环。这些滞回环的半径随着更高的敏感度而减小。较小的半径意味着车头时距或速度的振荡更小，即交通流的稳定性更高。 展示了经过t=19000秒后具有不同敏感度的密度波的时空演化。密度波的振幅随敏感度增加而减小。此外，密度波随时间向后传播。

从这些图中可以很容易地看出，通过更高的敏感度可以增强均匀自动驾驶汽车流的稳定性。

仿真2.2

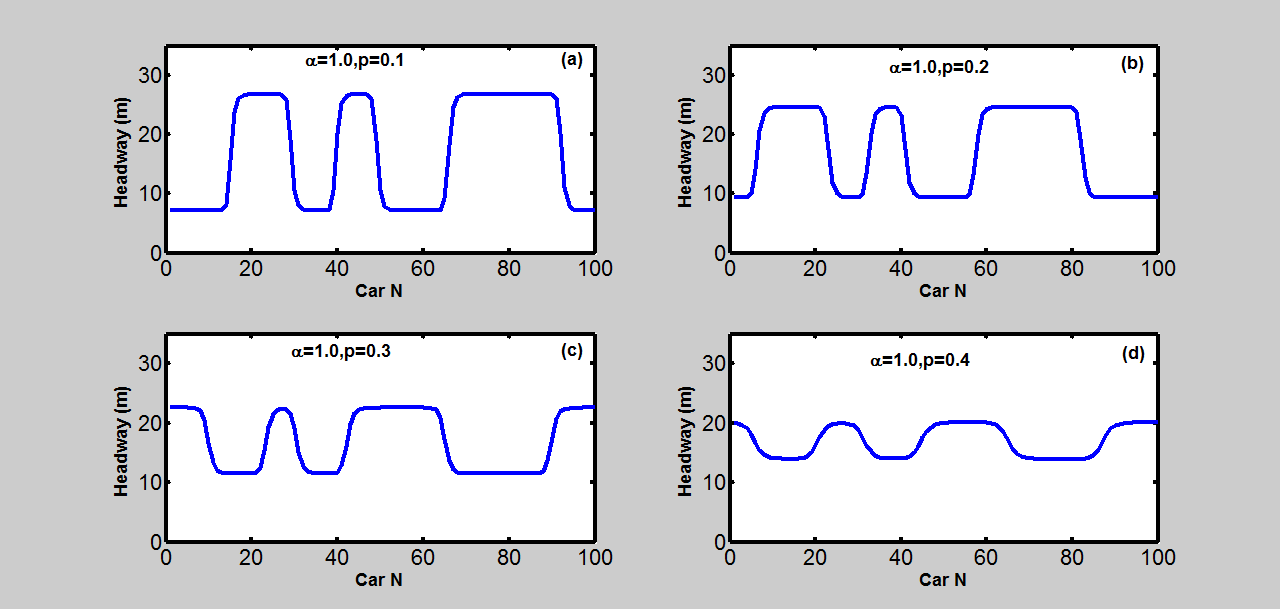
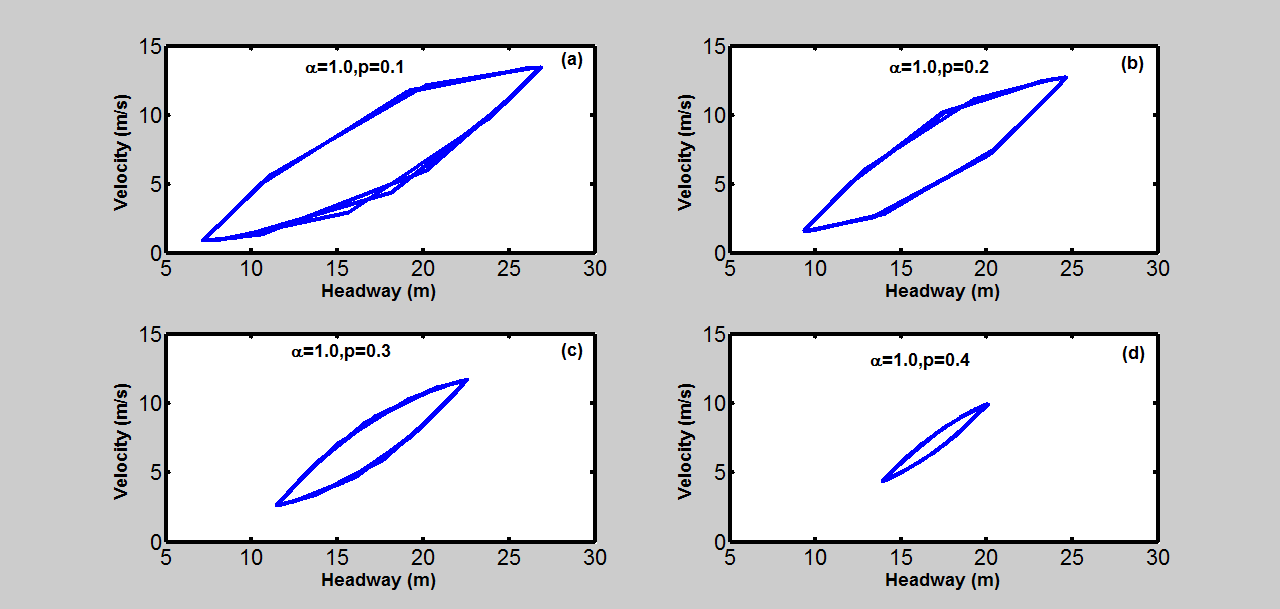
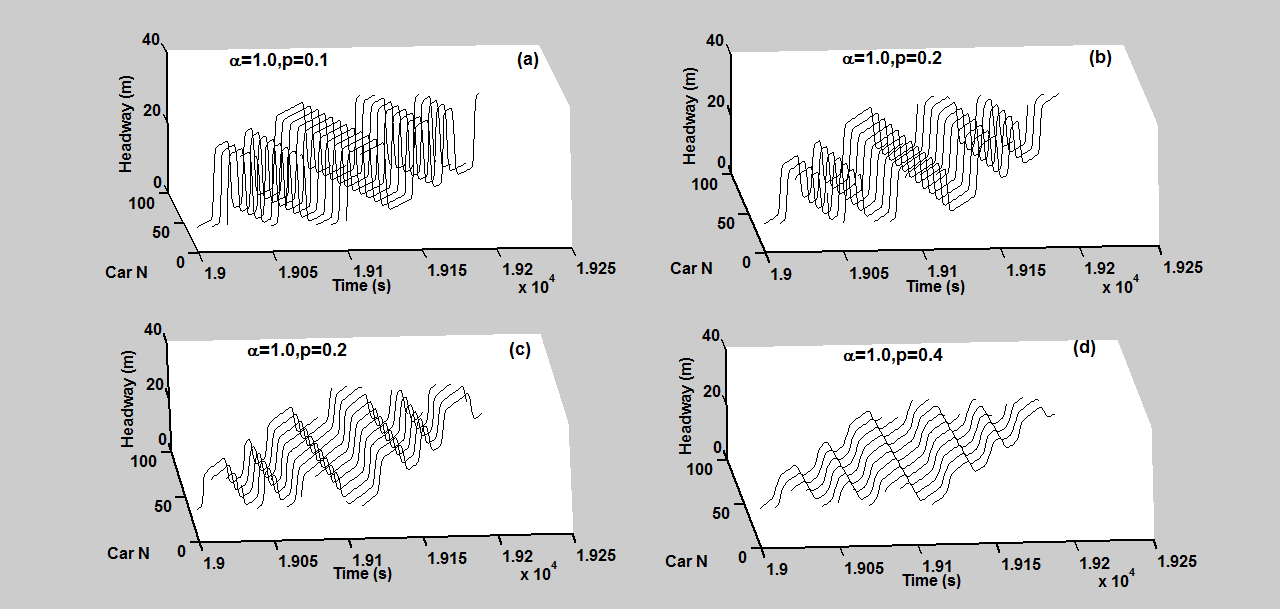
在此仿真中，敏感度取为$\alpha = 1.0$，平滑因子取为$p = 0.1, 0.2, 0.3, 0.4$。仿真结果如 至 所示。这些图中的(a)到(d)模式分别对应不同的平滑因子。 中的模式展示了在时间t=19000秒时，不同平滑因子下自动驾驶汽车的车头时距分布。从这些模式可以明显看出，随着平滑因子增大，自动驾驶汽车流的稳定性增强。这与 中的理论结果一致。 中的模式显示了不同平滑因子下自动驾驶汽车流的滞回环，其变化趋势与图2中的模式相符。滞回环的半径随着平滑因子的增加而减小。较大的半径意味着车头时距或速度的振荡更大，表明交通流的不稳定性更高。 展示了在t=19000秒后，不同平滑因子下密度波的时空演化。随着平滑因子的增加，密度波的振幅减小。此外，密度波随时间向后传播。

从这些图中可以很容易地看出，较大的平滑因子能够抑制均匀自动驾驶汽车流的交通拥堵。

仿真3

在本部分中，让我们检查混合交通流的稳定性的敏感度和平滑因子。在仿真中，混合交通流的总数为100，道路长度为1700米。不失一般性，人工驾驶汽车和自动驾驶汽车各占50%，并且所有车辆在道路上依次交替分布。人工驾驶汽车的驾驶员敏感度为$a = 0.85$。仿真3的持续时间为200000个时间步长。

仿真3.1

本模拟研究了传感器的不同敏感度对混合交通流稳定性的影响。由于平滑因子为零，自动驾驶汽车的后车头时距未被考虑。展示了不同敏感度下混合交通流在t=19000秒时的车头时距分布。展示了不同敏感度下混合交通流在t=19000秒后密度波的时空演化图。两图中的(a)到(d)模式分别对应不同的敏感度。从中可以看出，随着敏感度增大，车头时距振荡的振幅变得更小。这意味着混合交通流的稳定性随着敏感度的增加而增强。

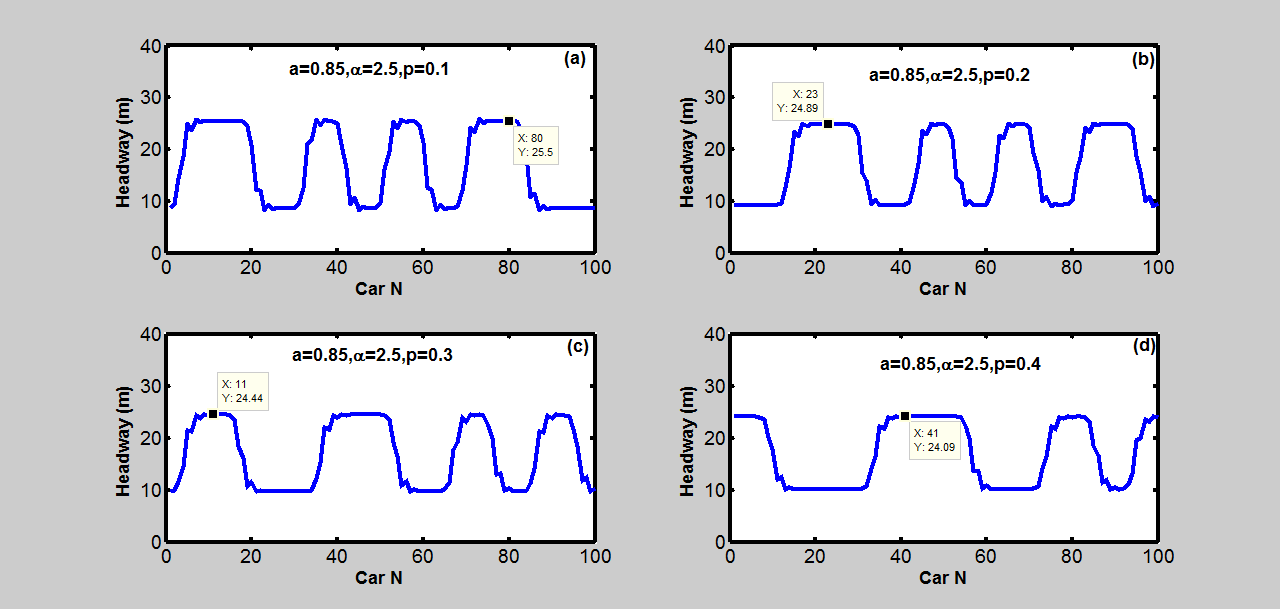
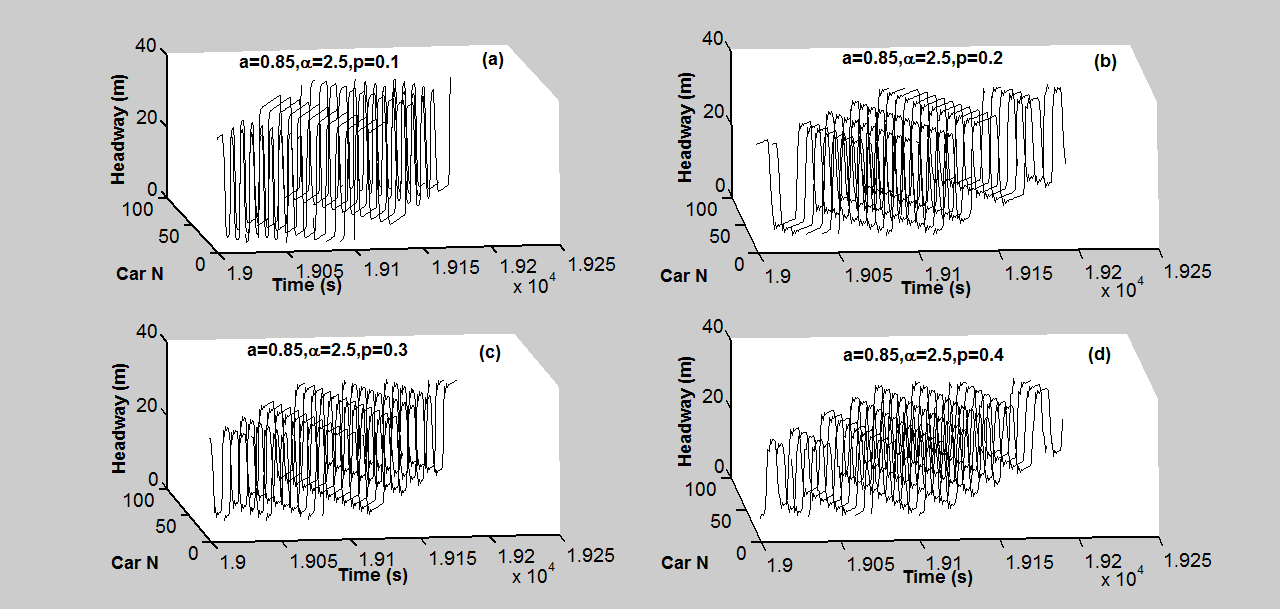
仿真3.2

本模拟研究了不同的平滑因子对混合交通流稳定性的影响。自动驾驶汽车的敏感度为$\alpha = 2.5$。展示了不同平滑因子下混合交通流在t=19000秒时的车头时距分布。展示了不同平滑因子下混合交通流在t=19000秒后密度波的时空演化图。两图中的(a)到(d)模式分别对应不同的平滑因子。从这些模式中可以发现，随着平滑因子增大，车头时距振荡的振幅变得更小。混合交通流的稳定性随着平滑因子的增加而增强。

4. 结论

本文对包含人工驾驶汽车和自动驾驶汽车的混合交通流进行了理论和数值研究。提出了一种具有可调灵敏度和平滑因子的自动驾驶汽车数学模型。基于一个定理进行了稳定性分析。通过数值模拟验证了理论结果。根据仿真结果得到了基本图。通过这些基本图可以发现存在一个临界点在密度‐流量曲线上，临界点之前，更高的敏感度、平滑因子以及自动驾驶汽车的混合比例可能会导致混合交通流产生更大的流量。而在临界点之后，则表现出相反的结果。此外，仿真数据显示了不同敏感度和平滑因子下的车头时距分布和滞回环。更高的敏感度和平滑因子增强了纯自动驾驶汽车流或混合交通流的稳定性。这些结果与理论分析结果高度一致。