python机器学习手写算法系列——决策树

本系列另一篇文章《线性回归》
https://blog.youkuaiyun.com/juwikuang/article/details/78420337

本文源代码地址：
https://github.com/juwikuang/machine_learning_step_by_step

你也可以直接看源代码，我用了jupyter notebook，源代码中有详细的说明。

数据集

数据来源于我的Github项目。 Data from here:

https://github.com/juwikuang/china_job_survey

我爬了全国的招聘信息，然后以上海为例子，选择了收入最高的25%和最低的25%，以他们作为两类。通过机器学习的分类模型，找出程序员如何成功（成为收入最高的25%）的秘诀。
最近正好朋友介绍了一本书，成功的公式。它也是通过大量数据，找出成功的公式的。我决心好好分析数据，找出程序员成功的Formula。

数据集已经通过GitHub共享。

字段说明

dataset 说明，

low=工资是否低，low=0表示高工资，low=1表示低工资。这是我们的label，或者说y，或者叫应变量。其他的叫features，或者叫X，或者叫自变量。

注意我这里y是小写，X是大写，因为y是vector，X是matrix

ageism=是否有年龄歧视，我检查招聘信息里面，是否有【岁】字，是则是年龄歧视。

career_algorithm, career_architect, career_software_engineer=这里对职业（career），进行了one-hot-encoding。

其他100多个feature就不一一解释了。这里并不是写论文，等他们出现了再说。

为了简单起见，所有的feature都是bool型的

决策树

决策树其实很容易理解，我们先看看相亲决策树吧。

对，这就是决策树。现在你有了感性认识了。

决策树Decision Tree(DT)，是通过某种选择机制（entropy或者gini），找到能够把数据分成正负两组的特征。往往需要多次划分，才能得到满意的结果，所以，最后得到的模型，看起来就像一颗树。所以叫决策树。

这个算法，概括的来说，就是不断的寻找一个最优解（最优特征+最优分割点），把数据集一分为二，使集合纯度最高（label为true的和false尽量分开），直到分了n层。

具体来说，就是：

加载数据，遍历每个特征，用每个特征去划分数据集。

这里的特征，可能是bool型的，那就最好了，true的一组，false的一组，直接分成了两组。

也可能是数值型的，那就要把数据从小到大排序，不断的增大切割点的数值，只到找到最优的解。

如果特征是字典型的（categorical，如天气分为晴天，阴天，下雨）的，现在一般是用one-hot-encoding转化成几个bool型。

每个特征的最优解，都是用entropy或者gini表示的，等遍历完了所有的特征，就比较他们的entrop或者gini，选出最优的。

用最优解把数据集一分为二，再对子数据集运用上面的步骤，直到决策树已经达到了一定深度。

决策树的flow chart

集合纯度

集合纯度是决策树的难点重点，我们需要找到一种数学方法，去计算集合的纯度。常用的有熵（entropy）和基尼（gini）。

Entropy

根据维基百科，信息熵（Information Entropy）的数学定义为：
The function from wikipedia:

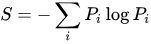
def information_entropy(counts):
    percentages = counts/np.sum(counts)
    S=0
    for p in percentages:
        if p==0:
            continue
        S=S-(p*np.log2(p))
    return S

这里p表示百分比，S表示信息熵。S越小，数据集的纯度越高。以我们的数据集为例，假如所有人都是高收入，则S等于0，这时S最小，数据集最纯。

information_entropy([0,1])

返回值0.0

information_entropy([1/2,1/2])

返回值1.0

我们的数据集呢？我们算一下

n_high=2244 #有2244人拿高工资
n_low=2647 #有2647人拿低工资
information_entropy([n_low, n_high])

返回值0.995

可见，信息熵接近于1，说明我们数据集的纯度非常低。 The information entropy is close to one, indicating it is very impure.

假如我们用会不会python，把数据集切开。

data_python=data[data.pl_python==1]
data_not_python=data[~data.pl_python==1]

def data_entropy