矩形覆盖

【题目】

我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

【分析】

n=1 只有横放一个矩形一种解决办法
n=2 有横放一个矩形，竖放两个矩形两种解决办法
n=3 在n=2的基础上加1个横向，n=1的基础上加2个竖向
n=4 在 n=3的基础上加1个横向，n=2的基础上加2个竖向

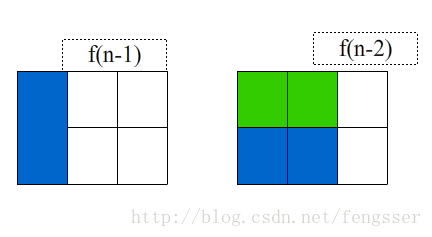
于是f(n) = f(n-1) + f(n-2),于是这又是一个斐波那契数列问题。

【代码】

    public static void main(String[] args) {        
        System.out.println(rectCover(3));//3
        System.out.println(rectCover1(3));//3
    } 

    //矩形覆盖
    //高效，动态规划
    public static int rectCover(int target){
        if(target<1) return 0;
        if(target==1) return 1;
        if(target==2) return 2;
        int[] dp=new int[2];
        dp[0]=1;
        dp[1]=2;
        int tmp=0;
        target-=2;
        while(target>0){
            tmp=dp[0]+dp[1];
            dp[0]=dp[1];
            dp[1]=tmp;
            target--;
        }
        return dp[1];
    }

    //低效，递归
    public static int rectCover1(int target){
        if(target<1) return 0;
        if(target==1) return 1;
        if(target==2) return 2;
        return rectCover1(target-1)+rectCover1(target-2);
    }

【关于动态规划】

　　动态规划的思想与我们上篇探讨的分治法相似，也是通过组合子问题的解从而得到整个问题的解。从上节给出的题目看得出来，分治分解出的子问题都是相对独立的，但是动态规划分解的子问题通常不是独立存在的。分治法有时候存在分解后的问题太多，因而重复计算也多的问题。那么如果能够保存已求得的子问题的答案，从而在再次使用的时候调出，就会节省大量的时间。我们可以用一个表（数组）来存放求得的子问题的解，这就是动态规划的思想。