随机过程-习题集1

1. 什么是随机过程？阐述其意义及内涵。
2. 写出随机过程$X(t)$的一、二维数字特征函数。
3. 基于随机过程$X(t)$的核心特征函数，给出其他的一、二维数字特征函数。
4. 设随机过程$X(t)=Ut$，$U$在$(0,1)$上均匀分布，通过计算该过程的一维和二维核心数字特征分析其数学模型的有效性。
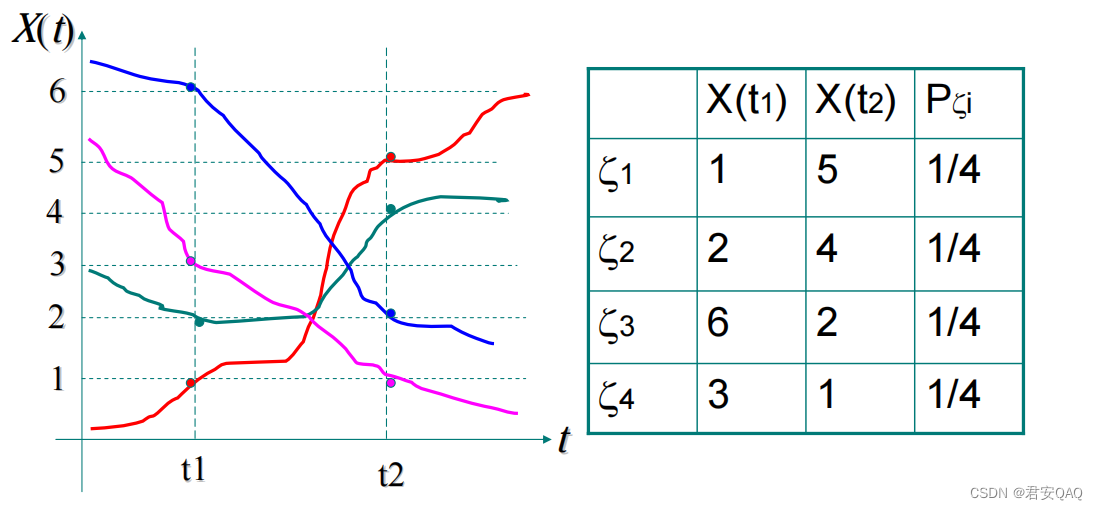
5. 分析下图中随机过程$X(t)$的观测模型的有效性；若无效，给出改进的方法。
6. 习题2.11：随机过程为$X(t)=A\cos ({\omega }_{0}t+\Phi )$,式中，${\omega }_0$为常数，$A$和$\Phi$是两个统计独立的均匀分布的随机变量。概率密度分别为$$p_A(a)=1,0\le a<1;p_{\Phi }(\phi )=\frac{1}{2\pi },0\le \phi <2\pi$$
   求X(t)的均值及自相关函数。分析其数学模型的有效性？如果可以有效的表征信号，分析其所表征的信号是确定信号还是随机信号？
7. 习题2.10：随机过程为$X(t)=A\cos ({\omega }_{0}t+\Phi )$,式中，${\omega }_0$为常数，$\Phi$是$(0,2\pi )$上均匀分布的随机变量。求$X(t)$的均值、方差和自相关函数。求证$X(t)$是宽平稳的。
8. 利用非周期平稳过程$X(t)$自协方差函数的数学模型，给出自协方差函数的四个性质
9. 分析随机过程$X(t,\xi )$时间平均与时间自相关函数的性质
10. 通过判别习题2.11中所示随机过程的各态历经性，分析其所表征的信号的抗干扰性
11. 例题3.4：$X(t)=A\cos ({\omega }_{0}t+\Phi )$是否为各态历经过程。并绘制出系统并简述工作原理。
12. 例题3.5：讨论随机过程$X(t)=Y$的各态历经性，Y是方差不为0的随机变量。
13. 习题3.12：随机过程$X(t)=A\cos ({\omega }_{0}t+\Phi )$，$A,{\omega }_0,\Phi$是统计独立的随机变量，其中A的均值为2，方差为4，$\Phi$在$(-\pi ,\pi )$上均匀分布，${\omega }_0在(-5,5)$上均匀分布，$X(t)$是否平稳？是否具有各态历经性，求出自相关函数，分析其所表征的信号为确定信号还是随机信号及其抗干扰性。
14. 关于随机信号的收敛性。
15. 用公式表示宽平稳随机过程X(t)和Y(t)在同一时刻的互不相关性，独立性。
16. 互相关函数$R_{XY}(0)=0$中的两个0分别表示什么？
17. 分析由实随机过程X(t)与复随机过程线性组合而成的随机信号，必须要确知这两个随机过程的哪些时域数字特征？
18. 随机过程$X(t)=a\cos ({\omega }_{0}t+\Phi )$，$a,{\omega }_0是常数，\Phi 是在(0,\frac{\pi }{2})$上均匀分布的随机变量，求平均功率W。并计算自功率谱密度。
19. 例题4.4：若平稳过程$X(t)$的功率谱密度为$G_X(\omega )$又有：$$Y(t)=aX(t)\cos {\omega }_{0}t$$式中，a为常数，求功率谱密度$G_Y(\omega )$
20. 绘制利用实测$R_{XY}(\tau )$获取线性时不变系统$h(t)$函数的系统结构图：并描述系统的工作条件。