IMC法设计不稳定多变量系统控制器

IMC方法控制不稳定多变量系统

摘要

在本研究中，采用矩阵表示法推导了内模控制的分散式和集中式PI控制器。对所得方程应用麦克劳林级数以获取控制器参数。在控制器设计过程中，使用过程传递函数矩阵的对角元素和全部元素；而在评估控制器性能时，则使用完整的过程传递函数矩阵。为展示所提出的分散式控制系统的性能，考虑了两个例子；为评估所提出的集中控制器的性能，考虑了一个例子。本文方法的性能与已有报道的方法进行了比较。

关键词 ：PI控制器；不稳定系统；麦克劳林级数；分散控制器；集中控制器

I. 引言

对于弱相互作用系统，分散式PI控制系统是足够的。多位研究人员建立了设计分散式控制系统的技术，包括解析法[2]、增益与相位裕度法[3]、最大对数模调谐（BLT）方法、等效传递函数（ETF）方法、有效相对增益阵列（ERGA）方法和相对归一化增益阵列（RNGA）方法。

南东提出了同步多回路（SML）调谐方法[4]。SML方法是一种包含启发式步骤和优化步骤的两阶段过程。

许斯克[6]建议采用基于相位裕度指标的分散控制器，其优点在于仅需一个整定参数，且为单步过程。然而，该方法的缺点包括不适用于具有强相互作用的系统，并且不允许精细调节。金等人[5]推荐使用非参数有效模型将多变量控制系统分解为若干个独立的标量系统，并采用非凸优化方案获取控制器参数。

李等人[2]将广义IMC‐PID调谐扩展到多变量系统，并使用分析技术（麦克劳林级数）来获得控制器参数。

BLT方法是由Luyben[6]提出的一种著名且广泛应用的技术。该方法利用齐格勒‐尼科尔斯（ZN）步骤针对对角传递函数计算控制器参数，并基于相互作用进行失谐步骤。这是一种试错技术，旨在实现鲁棒的稳定性和性能。

内模控制结构为标量系统提供了稳定且鲁棒的性能。

武等人[7]将IMC方法应用于多变量系统，其中分别对G、Gc和R应用麦克劳林级数，通过比较麦克劳林级数的多项式项得到最终的对角控制器。在当前方法中，获得了复杂的控制器项；为了提高性能并获得PI/PID控制器参数，我们在最后阶段仅应用一次麦克劳林级数。

本文提出了一种基于过程的逆和整定参数来设计分散式与集中式控制系统的技术，并采用分析技术计算所得的控制器参数。

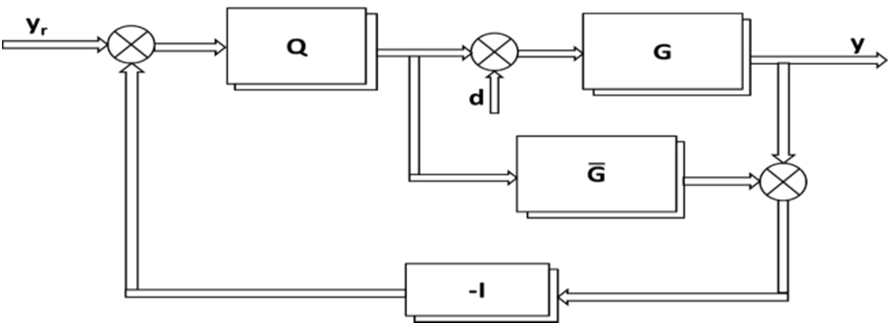
所提出的方法相较于其他方法具有良好响应，并产生较少交互且控制器输出行为有界。第2节讨论了为稳定系统设计分散式控制系统的详细步骤。在第3节中，通过两个例子测试了所提出的方法的有效性。最后，第4节给出了结论。

II. 多变量系统控制器设计

考虑一个具有时间延迟的双输入双输出（TITO）开环不稳定多变量系统。$G_p(s)$是过程传递函数矩阵，$G_c(s)$是分散控制器传递函数矩阵。被控对象的TITO传递函数矩阵为：

$$
G_P(s) = \begin{bmatrix}
g_{p,11}(s) & g_{p,12}(s) \
g_{p,21}(s) & g_{p,22}(s)
\end{bmatrix}
\quad (1)
$$

设过程传递函数矩阵的每个对角元素均用一个不稳定一阶加纯滞后模型（UFOPTD）表示，即

$$
g_{p,ij}(s) = \frac{k_{ij}}{\tau_{ij}s - 1} e^{-\theta_{ij}s}, \quad (2)
$$

这里，过程传递函数矩阵的非对角元素用稳定一阶加纯滞后模型（FOPTD）表示，即

$$
g_{p,ij}(s) = \frac{k_{ij}}{\tau_{ij}s + 1} e^{-\theta_{ij}s}, \quad \forall i,j \in 2, i \ne j \quad (3)
$$

分散控制器的结构如下所示：

$$
G_c(s) = \begin{bmatrix}
g_{c,1}(s) & 0 \
0 & g_{c,2}(s)
\end{bmatrix}
\quad (4)
$$

我们有：

$$
G_c = (I - QG_p)^{-1}Q \quad (5)
$$

并且，内模控制控制器（$Q$）与期望闭环传递函数矩阵及过程传递函数矩阵之间的关系如下所示

$$
R = QG_p \quad (6)
$$

假设$\hat{G}_p \approx G_p$，且控制器的关系由$G_p$给出，$R$的表达式如下所示

$$
G_c = G_p^{-1}(R^{-1} - I)R \quad (7)
$$

设计分散式控制系统时，仅考虑$G_p(s)$中的对角项，并假设每个回路（$i=1$到$n$）的闭环$nxn$系统遵循一阶响应 ($R$)。对于无时间延迟的过程，考虑

$$
R = (\gamma I + \tau_c s I + s^2 I)^{-1} \quad (8)
$$

将方程（8）代入方程（7）后，控制器方程（7）变为

$$
G_c = G_p^{-1}[(\gamma + \tau_c s + s^2)(I) - 1] \quad (9)
$$

类似地，对于$\theta/\tau \geq 0.2$，考虑

$$
R = [\gamma I + \tau_{iic} s I + e^{\theta_{ii}s} I]^{-1} \quad (10)
$$

控制器方程（7）变为

$$
G_c = G_p^{-1}[(\gamma + \tau_{iic} s + e^{\theta_{ii}s})(I) - 1][(1 + \gamma)e^{\theta_{ii}s}]^{-1} \quad (11)
$$

$\lambda_i$是可调的整定参数

$$
\tau_c = \begin{bmatrix}
\tau_{c11} & 0 \
0 & \tau_{c22}
\end{bmatrix}
\quad (12)
$$

将式（11）中$G_p$的对角元素和$\tau_{iic}$代入，得到一个复杂的方程。最后，对该结果方程应用麦克劳林级数并忽略高阶项，即可得到理想分散式PI控制器参数，如前一节所述（并在附录A中给出了一个符号程序示例）。

性能指标

为了分析控制系统的性能，采用以下性能指标：

$$
ISE = \int_0^\infty e(t)^2 dt \quad (13)
$$

$$
IAE = \int_0^\infty |e(t)| dt \quad (14)
$$

其中，$e(s)=r(s)-u(s)$。

鲁棒稳定性分析

当过程模型的参数包含不确定性时，多回路控制系统的稳定性鲁棒性变得更加重要。因此，采用最大奇异值不确定性模型来验证所提出的控制系统的稳定性鲁棒性。

首先，对于过程乘法输入不确定性$[I + \Delta_I(s)]G(s)$，若满足[8]，则闭环系统是稳定的。

$$
\sigma_1(\omega) < \frac{1}{|\Delta_I(j\omega)|} \quad (15)
$$

其中，$\sigma_1$是闭环系统${ G_c(j\omega)[I + G(j\omega)G_c(j\omega)]^{-1} }$的最大奇异值。对于过程输出不确定性$G(s)[I + \Delta_O(s)]$，闭环系统的稳定性鲁棒性可通过[9]得到。对于乘法输出不确定性，若满足以下条件，则闭环系统稳定

$$
\sigma_2(\omega) < \frac{1}{|\Delta_O(j\omega)|} \quad (16)
$$

其中$\Delta_I(s)$和$\Delta_O(s)$是稳定的，$\sigma_2$是闭环系统${ G_c(j\omega)[I + G(j\omega)G_c(j\omega)]^{-1} }$的最大奇异值。公式(15)和(16)右侧部分得到的频率图表示了闭环系统的稳定性边界。曲线下面积代表系统的稳定性，曲线下面积越大，表明系统具有更高的稳定性。通过该图可以方便地比较控制器的稳定性。曲线下面积最大的控制系统是最稳定的。

III. 仿真结果与讨论

例1

考虑以下不稳定系统：

$$
G(s) = \begin{bmatrix}
\frac{0.3960}{4.572s - 1}e^{-0.2s} & \frac{-0.585}{1.807s + 1}e^{-0.4s} \
\frac{1.7255}{2.174s + 1}e^{-0.2s} & \frac{1.9713}{1.801s - 1}e^{-0.4s}
\end{bmatrix}
\quad (18)
$$

所提出的分散式控制系统设置见表1。

表1：例1的分散式控制系统设置

	所提出的方法 $(\tau_{iic} = \tau_{ii})$
$K_c$	$\begin{bmatrix} 7.5956 & 0 \ 0 & 1.1579 \end{bmatrix}$
$\tau_I$	$\begin{bmatrix} 14.5458 & 0 \ 0 & 7.2859 \end{bmatrix}$

对于$d_1$或$d_2$的给定阶跃变化，也进行了干扰消除研究。响应结果如图4所示，相应的控制器输出变化如图5所示。

控制系统的鲁棒性通过Maciejowski[9]和Besta与Chidambaram[14]提出的方法进行评估。稳定性通过输入和输出乘法不确定性的逆最大奇异值来评估，如图6所示。

此外，图6还解释了分散控制器以及已报道的分散控制方案[11–13]具有类似的稳定性，并描绘了给定系统的稳定区域（曲线以下区域）和不稳定区域（曲线以上区域）。如前所述（在第2节中），所提出的分散控制系统在性能和稳定性方面优于已报道的分散控制系统[12–13]。

例2

考虑以下不稳定系统：

$$
G(s) = \begin{bmatrix}
\frac{1}{1.5s - 1}e^{-s} & \frac{-2.5}{1.5s + 1}e^{-s} \
\frac{-1}{1.4s + 1}e^{-s} & \frac{1}{4.2s - 1}e^{-s}
\end{bmatrix}
\quad (19)
$$

基于改进内模控制的分散式控制系统设置如表2所示。

表2：例2的控制器设置

	IMC‐分散式控制器 $(\tau_{iic}=5,2)$
$K_c$	$\begin{bmatrix} 2.1838 & 0 \ 0 & -3.2476 \end{bmatrix}$
$\tau_I$	$\begin{bmatrix} 13.6765 & 0 \ 0 & 5.7556 \end{bmatrix}$

图7显示了所提出的方法的响应和相互作用。所提出的方法提供了良好响应，且相互作用最小。对于$d_1$或$d_2$的给定阶跃变化，也进行了干扰消除研究。响应结果如图8所示。

例3

考虑以下示例：

$$
G_P(s) = \begin{bmatrix}
\frac{1.6667}{3.3333s - 1}e^{-0.8333s} & \frac{-1.6667}{3.3333s + 1}e^{-0.6667s} \
\frac{0.8333}{1.6667s + 1}e^{-0.6667s} & \frac{3.3333}{3.3333s - 1}e^{-0.3333s}
\end{bmatrix}
\quad (20)
$$

表3：建议的控制器设置

	IMC集中式控制器 $(\tau_{iic}=4\tau_{ii})$	IMC集中式控制器 $(\tau_{iic}=4\tau_{ii})$
$k_c$	$\begin{bmatrix} 1.3178 & 0.7971 \ 0.3160 & -0.6509 \end{bmatrix}$	$\begin{bmatrix} 1.5428 & 0.9257 \ 0.4925 & -0.6509 \end{bmatrix}$
$\tau_I$	$\begin{bmatrix} 41.0008 & 82.6658 \ 39.3342 & 80.9992 \end{bmatrix}$	$\begin{bmatrix} 14.6675 & 14.6675 \ 56.3325 & 80.9992 \end{bmatrix}$
$\tau_D$	$\begin{bmatrix} 0.4900 & 0.6675 \ 0.3891 & 0.4969 \end{bmatrix}$	$\begin{bmatrix} 0.46 & 0.46 \ 0.46 & 0.46 \end{bmatrix}$

推荐的控制器参数以及文献中报道的集中式控制器设置见表3。图9中设定点跟踪（$y_{r1}$和$y_{r2}$的阶跃变化）的响应和相互作用明显表明，所提出的控制系统产生振荡响应和更大的交互作用。BLT方法产生的响应与GC方法相比，相互作用更小且调节时间更短。针对$d_1$和$d_2$的阶跃变化，也开展了干扰消除的研究，响应结果如图10所示。

性能通过ISE和IAE进行评估，其数值见表4。与戈文达卡南和奇丹巴拉姆提出的现有集中控制器[10]相比，所提出的集中控制方案具有较少的相互作用。对于$y_{r1}$的阶跃变化，IAE值的总和从15.73减少到9.501（即减少了39.60%）；对于$y_{r2}$的阶跃变化，从18.88减少到10.86（即减少了42.48%），优于已报道的GC方法。当前IMC方法的整体性能与BLT方法[11]进行了比较。所提出的BLT集中控制系统表现出更优的性能。

表4：例3的积分和加权积分误差指标

Step变化 in	方法	ISE $y_1$	ISE $y_2$	ISE $y_1+y_2$	IAE $y_1$	IAE $y_2$	IAE $y_1+y_2$
$y_{r1}$	BLT	11.79	1.147	12.937	10.93	3.528	14.458
$y_{r1}$	IMC	32.63	3.426	36.056	28.79	9.501	38.291
$y_{r1}$	GC	13.58	4.346	17.926	16.74	15.73	32.47
$y_{r2}$	BLT	1.613	4.057	5.67	4.301	9.396	13.697
$y_{r2}$	IMC	4.768	63.12	67.888	10.86	58.15	69.01
$y_{r2}$	GC	6.259	18.12	24.379	18.88	33.5	52.38
$d_1$	BLT	15.29	3.821	19.111	13.28	6.64	19.92
$d_1$	IMC	71.63	32.57	104.2	44.84	43.97	88.81
$d_1$	GC	17.32	4.321	21.641	13.58	6.784	20.364
$d_2$	BLT	9.174	27.55	36.724	13.65	23.34	36.99
$d_2$	IMC	102.9	578.2	681.1	57.64	176.8	234.44
$d_2$	GC	38.91	108.1	147.01	47.24	78.73	125.97

BLT – 方法[11], 提出的内模控制方法，GC报告的方法 GC[10]方法

IV. 结论

提出了一种简单且鲁棒的方法，用于设计不稳定多变量系统的分散式与集中式控制系统。基于内模控制原理，将多变量理想控制系统表示为期望闭环响应和过程传递函数矩阵的稳定逆的形式。通过对控制系统的结果方程应用麦克劳林级数，得到对角和全阵PI控制器的参数。该方法可获得具有减少耦合的良好设定值跟踪响应，以及具有较小控制器输出行为的良好抗干扰能力。鲁棒性研究通过逆最大奇异值进行分析。