通信原理_1 信号与系统基础

一、介绍

现代通信原理一般是传输电信号。

香农模型：

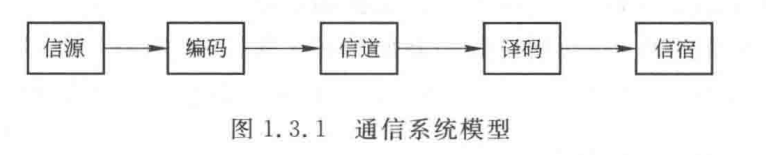
信源信息形式多种多样，编码时转换为处理更高效电信号。

信道一般有两种，第一种是在自由空间内传输的电磁波信号，第二种是沿导线传播的电磁波信号。

信道容量通常远大于用户传输的信息率。因此一般采用两种技术。

复用：多个信源的信号以正交的形式相互叠加，传输到目的地后再根据正交的原理拆分。

多址：多个信源的信号编码后直接传入信道，不叠加。

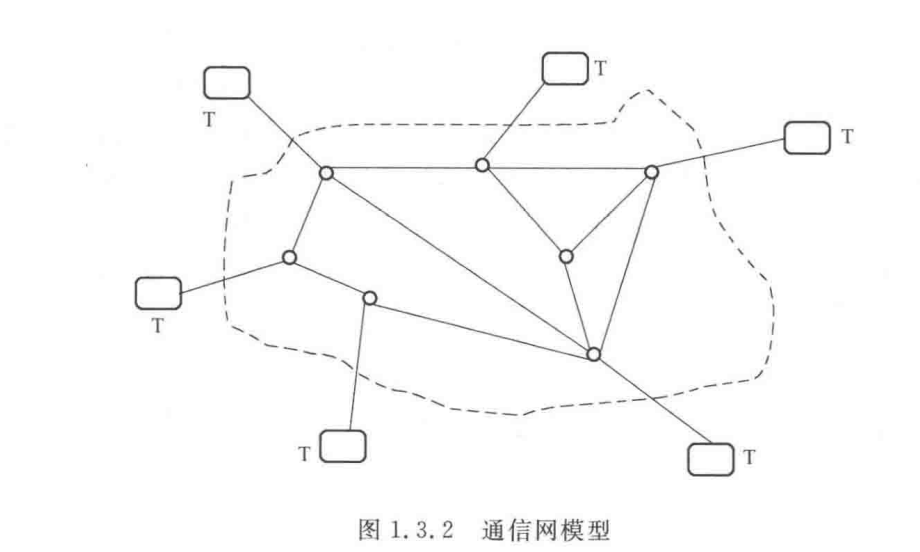
虚线代表通信网，中间的白点代表交换局，用于中转。

二、确定信号分析

能量 功率

能量：${\int }_{-\infty }^{+\infty }{s}^2(t)dt$

瞬时功率：$s^2(t)$

时移不改变能量和功率；信号*常数K，能量和功率都 *K^2.

一个信号的能量和功率不可能同时>0&&<无穷。能量有限的信号是能量信号，功率有限的信号是功率信号。

欧拉公式

$e^{j\theta }=cos\theta +jsin\theta$

复单频信号的频率：$e^{j2\pi ft}$，f就是频率。

复信号的能量和功率是两个实信号的能量和功率之和。

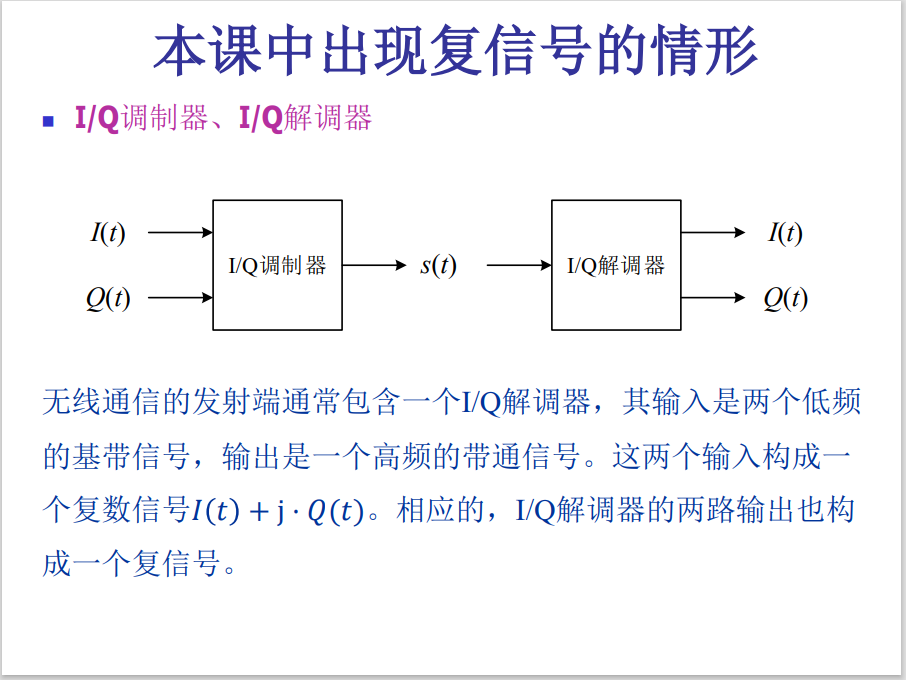
傅里叶级数和傅里叶变换

$ x(t)↔\int_{-\infty}^{{+\infty}X(f)e}{j2\pi ft}df $

$ X(f)↔\int_{-\infty}^{{+\infty}x(t)e}{-j2\pi ft}dt $

常用傅氏变换及性质

一个域中的面积是另一个域中原点处的值。

$ X(0)=\int_{-\infty}^{+\infty}x(t)dt $

$ x(0)=\int_{-\infty}^{+\infty}X(f)df $

时域越宽，频域越窄；时域越窄，频域越宽。

矩形傅氏变换

$$rect(fT)\leftrightarrow \frac{1}{T}sinc(\frac{t}{T})$$

冲激与直流

$$\delta (t)\leftrightarrow 1$$

$$1\leftrightarrow \delta (f)$$

时移与频移

$$x(t-t_0)\leftrightarrow X(f)e^{-j2\pi f{t}_0}$$

$$x(t)e^{j2\pi f_{0}t}\leftrightarrow X(f-f_0)$$

镜像和共轭对称性

x(t)↔X(-f)

$ x^*(t)↔X*(-f) $

因此如果x(t)是实信号，X(f)=X*(-f)，满足共轭对称。

卷积与乘积

一个域的乘积，是另一个域的卷积。

冲激函数的乘积和卷积：

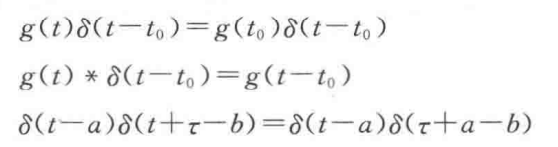
符号函数

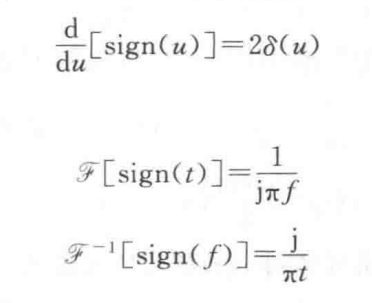
积分和微分

复单频信号和周期信号

$ e^{-j2\pi vt} $是复单频信号。

周期冲激序列

理想采样