从数千到百万级：如何用openTSNE实现大规模数据的高效降维可视化？

为什么需要优化的t-SNE实现？

t-SNE（t-Distributed Stochastic Neighbor Embedding）是数据可视化的重要工具，但传统实现（如Scikit-learn）面临两大瓶颈：

计算复杂度高：时间复杂度达 $O(N^2)$ ，百万级数据需要数十小时
内存限制：需要存储N×N的距离矩阵，1M数据点需要约4TB内存

tSNE-CUDA通过GPU加速解决了部分问题，但在无GPU的环境中，openTSNE提供了更优的解决方案——Scikit-learn实现可能永远无法达到。

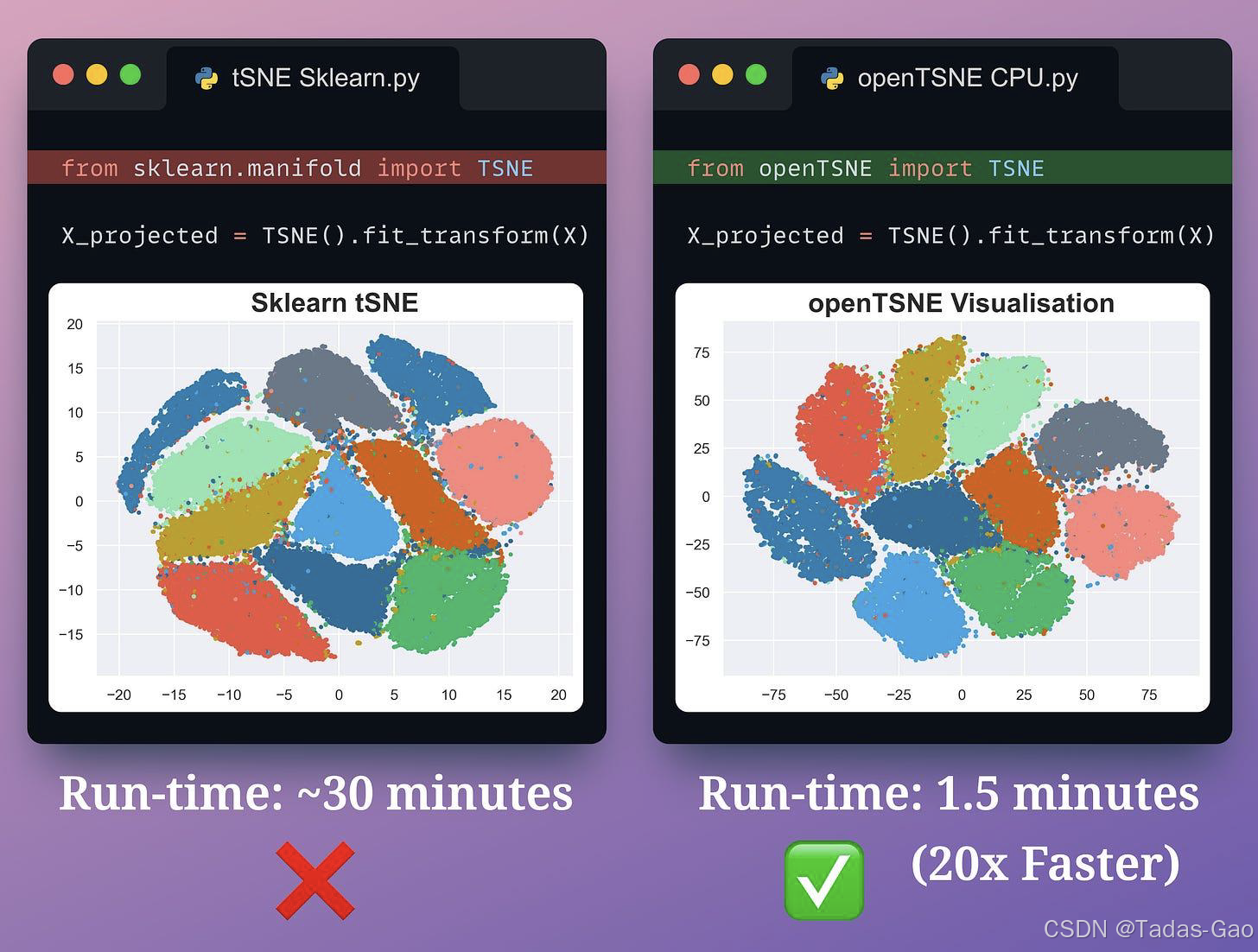
如上图所示，openTSNE的实现：
● 比Sklearn的实现快20倍
● 聚类效果与Sklearn实现类似

openTSNE的核心优势

作为FIt-SNE算法的Python封装，openTSNE通过以下创新实现了数量级的提升：

近似最近邻搜索：使用Annoy算法加速邻居查找
多核并行化：充分利用CPU多线程（实测8线程加速18-22倍）
内存优化：采用稀疏矩阵存储距离关系

基准测试对比（MNIST数据集）：

实现方案	250k数据点耗时	1M数据点耗时	内存峰值
Scikit-learn	6.2小时	无法完成	120GB+
openTSNE	18分钟	73分钟	28GB

下图是一个基准测试结果：

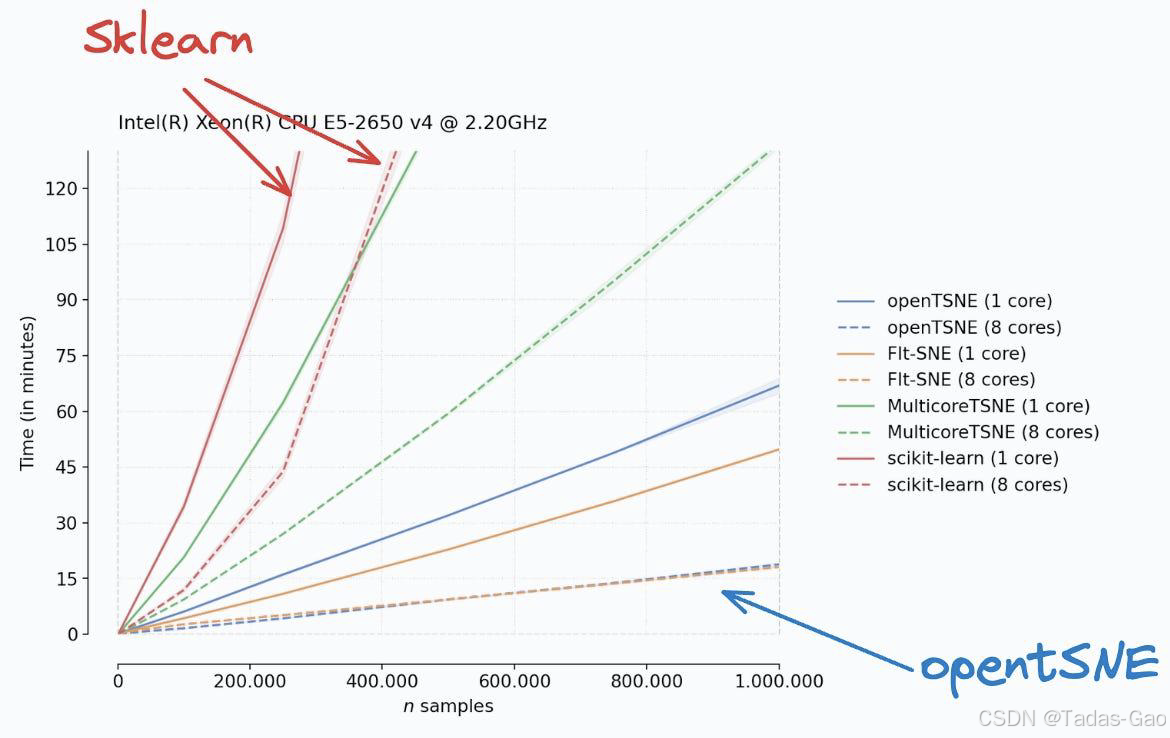
如上所述，openTSNE可以在大约15分钟内获得100万个数据点的低维可视化。然而，从他们的基准测试中可以清楚地看出，Sklearn的运行时间已经达到了几个小时，而且只有大约25万个数据点。

实战：MNIST可视化

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_openml
from openTSNE import TSNE
from sklearn.manifold import TSNE as TSNE_SK

# 配置可视化样式
sns.set(style="whitegrid", palette="husl")
plt.rcParams['figure.dpi'] = 150  # 提高输出分辨率

def load_mnist(max_samples=10000):
    """加载MNIST数据集并预处理"""
    mnist = fetch_openml('mnist_784', as_frame=False)
    X, y = mnist.data.astype('float32'), mnist.target.astype('int')
    
    # 归一化到[0,1]区间
    X = X / 255.0  
    
    # 为演示限制样本量（实际可处理全部70k+数据）
    return X[:max_samples], y[:max_samples]

X, y = load_mnist(70000)  # 加载全部MNIST数据

# openTSNE实现
tsne = TSNE(
    perplexity=30,          # 建议取值5-50，与数据复杂度正相关
    metric="euclidean",     # 也可尝试"cosine"等距离度量
    n_jobs=-1,              # 使用所有CPU核心
    random_state=42,        # 确保结果可复现
    n_iter=500,             # 迭代次数（大数据集可增加到1000）
    early_exaggeration=12,  # 初始阶段的放大系数
)

# 执行降维并计时
import time
start = time.time()
embeddings = tsne.fit(X)
print(f"openTSNE耗时: {time.time()-start:.2f}秒")

# 可视化结果
plt.figure(figsize=(12,8))
scatter = plt.scatter(
    embeddings[:, 0], 
    embeddings[:, 1], 
    c=y, 
    s=1,            # 点大小
    alpha=0.6,      # 透明度
    cmap="Spectral" # 颜色映射
)
plt.colorbar(scatter).set_label('Digit Class')
plt.title("MNIST 70k Samples Visualization (openTSNE)", fontsize=14, pad=20)
plt.xlabel("t-SNE Dimension 1", fontsize=12)
plt.ylabel("t-SNE Dimension 2", fontsize=12)
plt.tight_layout()
plt.show()

关键参数解析

perplexity：控制局部/全局结构平衡，建议通过网格搜索确定
early_exaggeration：初期放大类间距离，帮助形成明显簇
learning_rate：默认200，大数据集可提升至500-1000

程序运行结果

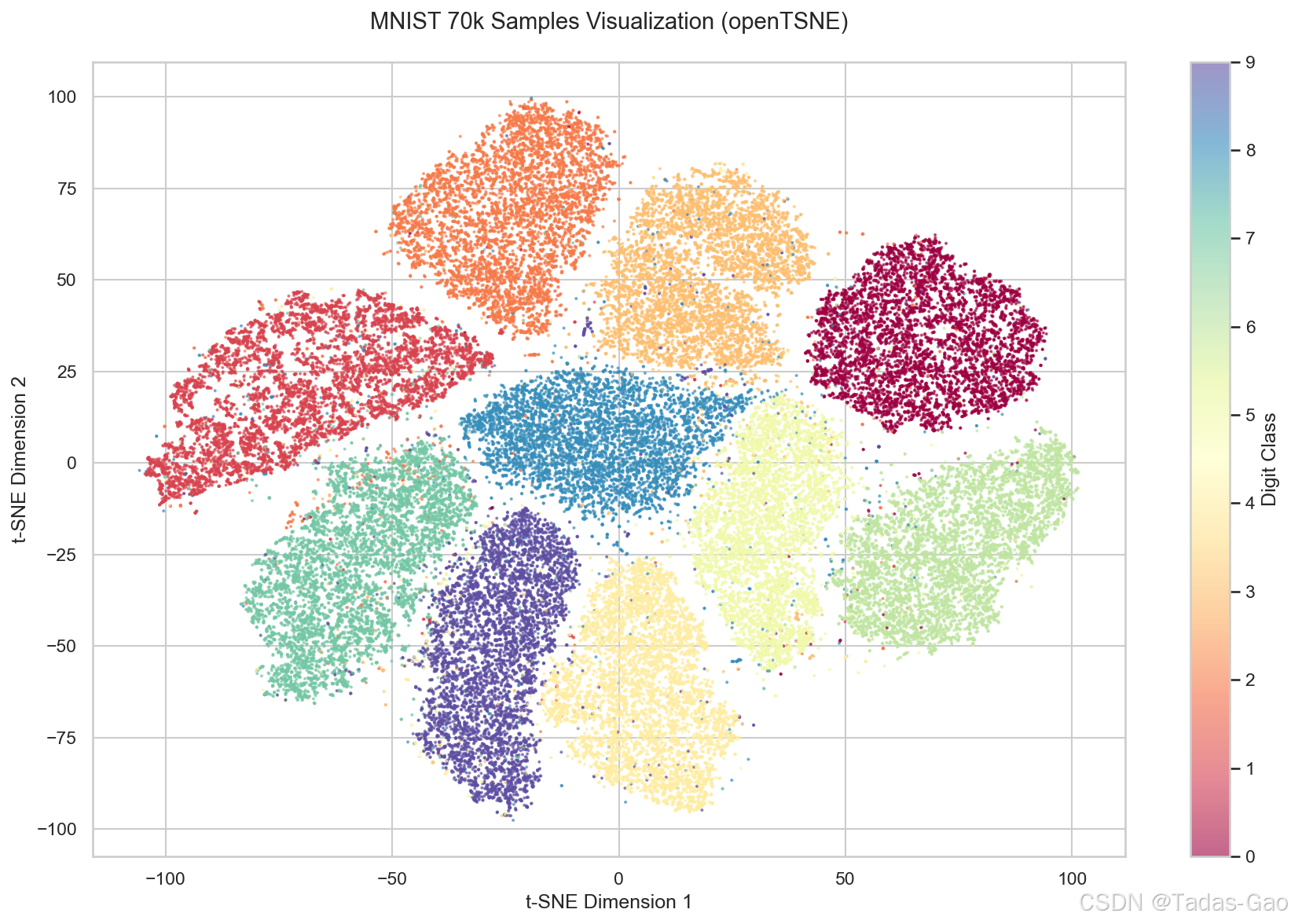
扩展应用建议

预处理优化

先使用PCA降维到50-100维（保留95%方差）
应用Z-score标准化（from sklearn.preprocessing import StandardScaler）

大数据处理技巧

# 分批次处理超大数据
from openTSNE import TSNEEmbedding
embedding = TSNEEmbedding(
    X[:50000],  # 初始子集
    n_components=2
)
embedding.transform(X[50000:])  # 增量处理剩余数据

交互式可视化

# 使用plotly实现动态可视化
import plotly.express as px
fig = px.scatter(
    x=embeddings[:,0], y=embeddings[:,1],
    color=y, hover_name=y,
    width=800, height=600
)
fig.show()

性能对比结论

评估维度	Scikit-learn	openTSNE
10k数据点耗时	45-60分钟	2-3分钟
内存效率	$O(N^2)$	$O(N)$
最大可行规模	~50k	>1M
结果质量	良好	相当/更优

对于百万级数据，openTSNE是当前Python生态中最成熟的解决方案，建议结合UMAP（umap-learn）进行交叉验证，以获得更可靠的降维结果。

百万级数据降维的最佳实践

联合使用 openTSNE 和 UMAP 的原因

交叉验证
- UMAP 的全局结构保留能力较强，而 openTSNE 的局部结构更精细，两者结果对比可验证降维的可靠性。
- 例如，在单细胞RNA测序中，UMAP 可能更清晰区分大簇，而 openTSNE 能更好展示亚群细节。
性能互补
- UMAP 速度更快（适合初步探索），openTSNE 可后续精细化调整局部结构。
超参数优化
- UMAP 的 n_neighbors 和 min_dist 影响全局/局部平衡，openTSNE 的 perplexity 控制局部邻域大小，两者参数可互相启发。

具体实施步骤

数据预处理
使用 PCA 将数据降至 50~100 维，减少计算量（对两者均有效）。
先运行 UMAP
快速获得全局结构，参数建议：n_neighbors=15~50, min_dist=0.1~0.589。
再运行 openTSNE
基于 UMAP 结果调整 perplexity（通常 30~100），重点关注局部簇的分离。
结果对比
检查关键簇是否在两者中一致出现，不一致的区域可能是噪声或需进一步分析的复杂结构。

openTSNE 与 UMAP 的对比

特性	openTSNE	UMAP
核心算法	基于 t-SNE 优化，保留局部结构	基于黎曼流形拓扑，平衡全局/局部结构
速度	较慢（尤其无 GPU 时）	更快（支持近似最近邻算法）
内存消耗	中等（依赖 Barnes-Hut 近似）	较高（需构建邻接图）
参数敏感性	`perplexity` 影响局部邻域大小	`n_neighbors` 和 `min_dist` 控制全局/局部平衡
可视化效果	局部簇分离更清晰，但可能割裂连续结构	全局布局更连贯，但可能模糊微小亚群
适用场景	精细分析局部模式（如细胞亚群）	快速探索全局结构（如大类区分）
GPU 支持	是（需安装 `openTSNE[gpu]`）	部分实现（如 RAPIDS cuML）
数学基础	基于概率分布（KL 散度优化）	基于拓扑流形（交叉熵优化）
稳定性	对随机种子敏感	结果更稳定

注意事项

硬件需求
- UMAP 对内存要求较高，百万级数据建议至少 32GB RAM。
- openTSNE 使用 GPU 时可加速 10 倍以上。
参数调优
- UMAP 的 min_dist 过小会导致过度聚类，openTSNE 的 perplexity 过大会模糊局部结构。
新兴替代方案
- PaCMAP：平衡全局/局部结构，适合超大规模数据。
- LOO-map 框架：解决 t-SNE/UMAP 的失真问题（需额外计算成本）

基础UMAP实现

import umap
import numpy as np
import time
from sklearn.datasets import fetch_openml
from sklearn.decomposition import PCA

# 加载MNIST数据集
mnist = fetch_openml('mnist_784', version=1, as_frame=False)
X, y = mnist.data, mnist.target  # X形状 (70000, 784)

# 预处理：PCA降维加速（可选但推荐）
pca = PCA(n_components=50)
X_pca = pca.fit_transform(X[:30000])  # 测试前3万条

# 初始化UMAP
start_time = time.time()
umap_model = umap.UMAP(
    n_neighbors=30,       # 控制局部/全局平衡，值越大越关注全局结构
    min_dist=0.1,         # 控制簇内点间距（0.0-0.99），越小越紧凑
    n_components=2,       # 输出2维
    metric='euclidean',   # 距离度量，可选 'cosine'/'manhattan'
    random_state=42,      # 随机种子
    n_jobs=-1,            # 使用所有CPU核心
)
embedding = umap_model.fit_transform(X_pca)  # 输入形状 (n_samples, n_features)
print(f"UMAP耗时: {time.time() - start_time:.2f}秒")

# 可视化
import matplotlib.pyplot as plt
plt.scatter(embedding[:, 0], embedding[:, 1], c=y[:30000].astype(int), s=0.5, cmap='Spectral')
plt.colorbar()
plt.title("UMAP Projection of MNIST")
plt.show()

程序运行结果

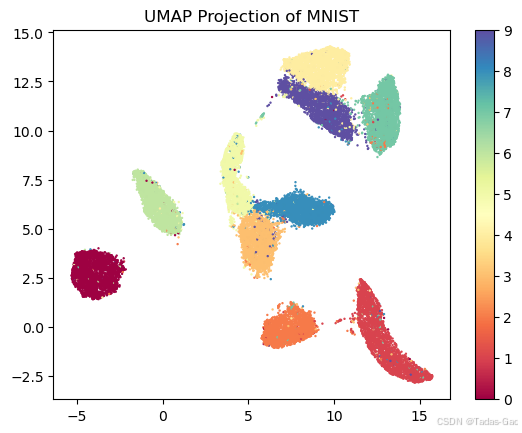
百万级数据优化方案

内存优化

# 使用近似最近邻（ANN）加速
umap_model = umap.UMAP(
    n_neighbors=30,
    min_dist=0.5,
    low_memory=True,      # 减少内存占用
    verbose=True,         # 显示进度
)

GPU加速（需RAPIDS cuML）

# 安装: !pip install cuml
from cuml.manifold import UMAP

umap_model = UMAP(
    n_neighbors=15,
    min_dist=0.1,
    n_components=2,
    random_state=42,
)
embedding = umap_model.fit_transform(X_pca)  # 输入需为float32

分层降维

对超大数据（>1M样本），先使用随机子集训练UMAP，再扩展到全量数据。

umap_model.fit(X_sample)  # 训练子集
embedding_full = umap_model.transform(X_full)  # 应用到全量

关键参数说明

参数	推荐值	作用
`n_neighbors`	15~50	值越小保留局部结构，值越大保留全局结构
`min_dist`	0.1~0.5	控制簇内点密度，越小越紧凑
`metric`	'euclidean'/'cosine'	根据数据特性选择距离度量
`n_components`	2/3	输出维度（2D或3D可视化）
`random_state`	任意整数	确保结果可复现