10 个最常用的损失函数

最新推荐文章于 2025-07-01 15:21:09 发布

架构进化论

最新推荐文章于 2025-07-01 15:21:09 发布

阅读量747

点赞数 21

CC 4.0 BY-SA版权

分类专栏： AI大模型文章标签：人工智能大模型机器学习 LLM

本文链接：https://blog.youkuaiyun.com/jsntghf/article/details/148428384

AI大模型专栏收录该内容

106 篇文章

订阅专栏

下图展示了一些回归和分类任务中常用的损失函数。

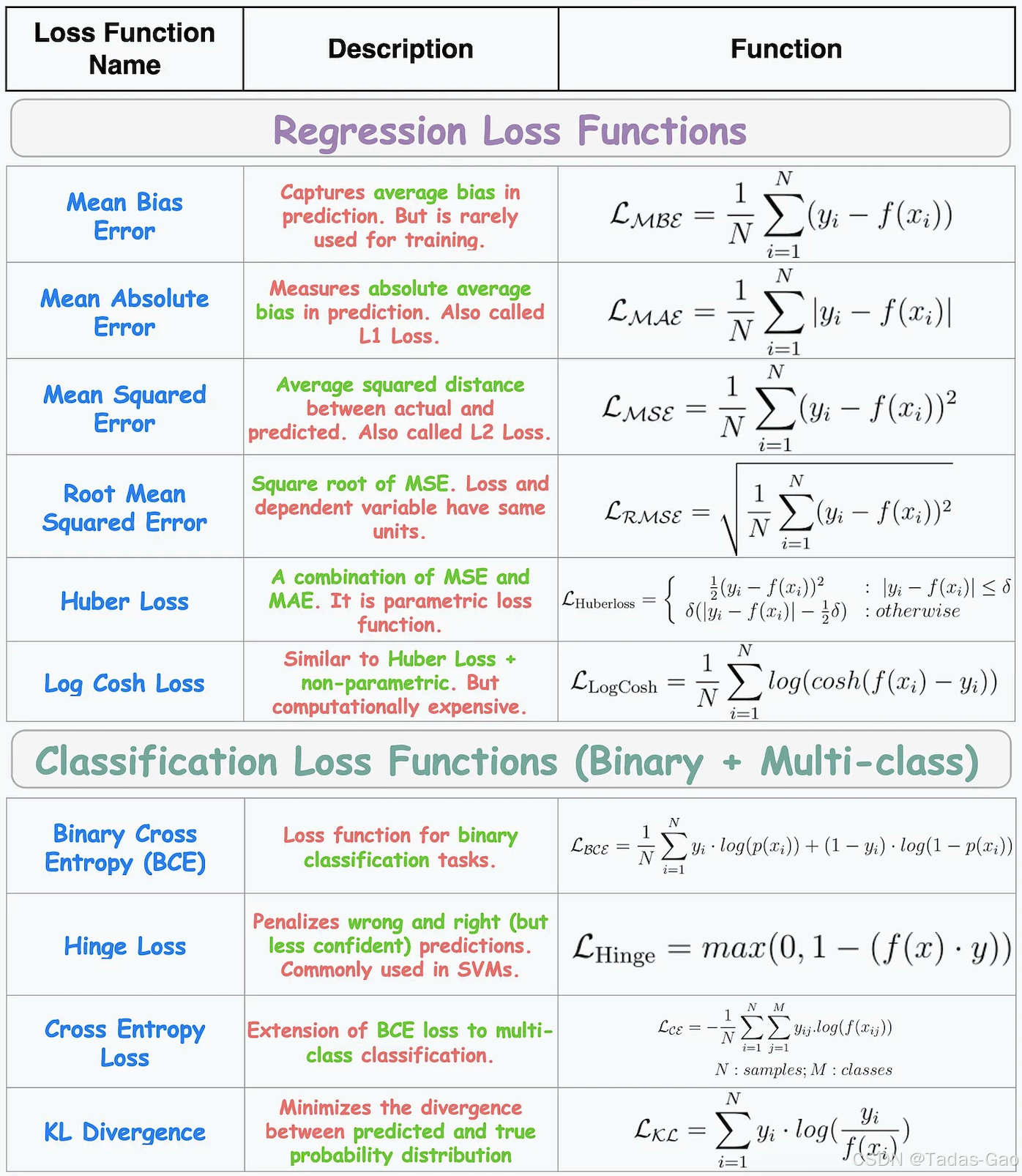
1. Mean Bias Error (MBE，平均偏差误差)

公式：
$\text{MBE} = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)$
特点：
反映预测值的平均偏差，方向敏感（正负误差可能相互抵消）。
用途：
用于需要检测系统偏差的场景（如金融预测），但通常不单独作为优化目标。

PyTorch 版本

import torch

def mean_bias_error(output, target):
    return (output - target).mean()

outputs = torch.tensor([1.5, 2.0, 3.1])
targets = torch.tensor([1.0, 2.5, 3.0])
loss = mean_bias_error(outputs, targets)
print("PyTorch MBE:", loss.item())

TensorFlow 版本

import tensorflow as tf

def mean_bias_error(output, target):
    return tf.reduce_mean(output - target)

outputs = tf.constant([1.5, 2.0, 3.1])
targets = tf.constant([1.0, 2.5, 3.0])
loss = mean_bias_error(outputs, targets)
print("TensorFlow MBE:", loss.numpy())

2. Mean Absolute Error (MAE，平均绝对误差)

公式：
$\text{MAE} = \frac{1}{n} \sum_{i=1}^n |y_i - \hat{y}_i|$
特点：
对异常值鲁棒，梯度恒定，可能导致收敛慢。
用途：
回归任务，尤其是数据存在离群点时。

PyTorch 版本

mae_loss = torch.nn.L1Loss()
loss = mae_loss(outputs, targets)
print("PyTorch MAE:", loss.item())

TensorFlow 版本

mae_loss = tf.keras.losses.MeanAbsoluteError()
loss = mae_loss(targets, outputs)
print("TensorFlow MAE:", loss.numpy())

3. Mean Squared Error (MSE，均方误差)

公式：
$\text{MSE} = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2$
特点：
放大较大误差，对异常值敏感，梯度随误差增大而增大。
用途：
回归任务，重视大误差的场景（如房价预测）。

PyTorch 版本

mse_loss = torch.nn.MSELoss()
loss = mse_loss(outputs, targets)
print("PyTorch MSE:", loss.item())

TensorFlow 版本

mse_loss = tf.keras.losses.MeanSquaredError()
loss = mse_loss(targets, outputs)
print("TensorFlow MSE:", loss.numpy())

4. Root Mean Squared Error (RMSE，均方根误差)

公式：
$\text{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2}$
特点：
与MSE相同，但量纲与原始数据一致，解释性更强。
用途：
同MSE，但需保持量纲一致时使用。

PyTorch 版本

def rmse(output, target):
    return torch.sqrt(torch.nn.MSELoss()(output, target))

loss = rmse(outputs, targets)
print("PyTorch RMSE:", loss.item())

TensorFlow 版本

def rmse(output, target):
    return tf.sqrt(tf.keras.losses.MSE(target, output))

loss = rmse(outputs, targets)
print("TensorFlow RMSE:", loss.numpy())

5. Huber Loss (胡贝尔损失)

公式：
$L_\delta(y, \hat{y}) = \begin{cases} \frac{1}{2}(y - \hat{y})^2 & \text{if } |y - \hat{y}| \leq \delta \\ \delta |y - \hat{y}| - \frac{1}{2}\delta^2 & \text{otherwise} \end{cases}$
特点：
结合MAE和MSE，对异常值鲁棒且收敛稳定。
用途：
回归任务，尤其是数据存在少量离群点时。

PyTorch 版本

huber_loss = torch.nn.HuberLoss(delta=1.0)
loss = huber_loss(outputs, targets)
print("PyTorch Huber Loss:", loss.item())

TensorFlow 版本

huber_loss = tf.keras.losses.Huber(delta=1.0)
loss = huber_loss(targets, outputs)
print("TensorFlow Huber Loss:", loss.numpy())

6. Log Cosh Loss (对数双曲余弦损失)

公式：
$\text{LogCosh}(y, \hat{y}) = \sum_{i=1}^n \log\left(\cosh(y_i - \hat{y}_i)\right)$
特点：
近似Huber Loss，二阶可导，光滑优化。
用途：
需要平滑梯度的回归任务（如深度学习）。

PyTorch 版本

def log_cosh_loss(output, target):
    return torch.log(torch.cosh(output - target)).mean()

loss = log_cosh_loss(outputs, targets)
print("PyTorch LogCosh Loss:", loss.item())

TensorFlow 版本

logcosh_loss = tf.keras.losses.LogCosh()
loss = logcosh_loss(targets, outputs)
print("TensorFlow LogCosh Loss:", loss.numpy())

7. Binary Cross Entropy (二元交叉熵)

公式：
$L(y, \hat{y}) = -\frac{1}{n} \sum_{i=1}^n \left[y_i \log(\hat{y}_i) + (1-y_i) \log(1-\hat{y}_i)\right]$
特点：
分类任务的标准损失，对概率预测敏感。
用途：
二分类问题（如垃圾邮件检测）。

PyTorch 版本

bce_outputs = torch.sigmoid(torch.randn(3))  # 模拟概率输出
bce_targets = torch.tensor([1., 0., 1.])    # 二进制标签
bce_loss = torch.nn.BCELoss()
loss = bce_loss(bce_outputs, bce_targets)
print("PyTorch BCE:", loss.item())

TensorFlow 版本

bce_outputs = tf.random.normal([3])
bce_targets = tf.constant([1., 0., 1.])
bce_loss = tf.keras.losses.BinaryCrossentropy(from_logits=False)
loss = bce_loss(bce_targets, tf.sigmoid(bce_outputs))
print("TensorFlow BCE:", loss.numpy())

8. Hinge Loss (合页损失)

公式：
$L(y, \hat{y}) = \frac{1}{n} \sum_{i=1}^n \max\left(0, 1 - y_i \hat{y}_i\right) \quad \text{where } y_i \in \{-1,1\}$
特点：
强调分类边界，用于支持向量机（SVM）。
用途：
二分类任务，尤其是支持向量机。

PyTorch 版本

hinge_outputs = torch.randn(3)
hinge_targets = torch.tensor([1., -1., 1.])  # 标签应为 +1/-1
hinge_loss = torch.nn.HingeEmbeddingLoss()
loss = hinge_loss(hinge_outputs, hinge_targets)
print("PyTorch Hinge Loss:", loss.item())

TensorFlow 版本

hinge_outputs = tf.random.normal([3])
hinge_targets = tf.constant([1., -1., 1.])
hinge_loss = tf.keras.losses.Hinge()
loss = hinge_loss(hinge_targets, hinge_outputs)
print("TensorFlow Hinge Loss:", loss.numpy())

9. Cross Entropy Loss (交叉熵损失)

公式：
$L(y, \hat{y}) = -\frac{1}{n} \sum_{i=1}^n \sum_{c=1}^C y_{i,c} \log(\hat{y}_{i,c}) \quad \text{(for } C \text{ classes)}$
特点：
多分类任务的标准损失，优化类别概率分布。
用途：
多分类问题（如手写数字识别）。

PyTorch 版本

ce_outputs = torch.randn(3, 5)  # 3样本5类别
ce_targets = torch.tensor([1, 0, 4])  # 类别索引
ce_loss = torch.nn.CrossEntropyLoss()
loss = ce_loss(ce_outputs, ce_targets)
print("PyTorch Cross Entropy:", loss.item())

TensorFlow 版本

ce_outputs = tf.random.normal([3, 5])
ce_targets = tf.constant([1, 0, 4])
ce_loss = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
loss = ce_loss(ce_targets, ce_outputs)
print("TensorFlow Cross Entropy:", loss.numpy())

10. KL Divergence (Kullback-Leibler散度)

公式：
$D_{\text{KL}}(P \parallel Q) = \sum_{i} P(i) \log \left( \frac{P(i)}{Q(i)} \right)$
特点：
衡量两个概率分布的差异，非对称性。
用途：
生成模型（如VAE）、分布对齐。

PyTorch 版本

kl_outputs = torch.log_softmax(torch.randn(3, 5), dim=1)  # 对数概率
kl_targets = torch.softmax(torch.randn(3, 5), dim=1)      # 目标概率
kl_loss = torch.nn.KLDivLoss(reduction='batchmean')
loss = kl_loss(kl_outputs, kl_targets)
print("PyTorch KL Divergence:", loss.item())

TensorFlow 版本

kl_outputs = tf.math.log(tf.nn.softmax(tf.random.normal([3, 5]), axis=1)
kl_targets = tf.nn.softmax(tf.random.normal([3, 5]), axis=1)
kl_loss = tf.keras.losses.KLDivergence()
loss = kl_loss(kl_targets, kl_outputs)
print("TensorFlow KL Divergence:", loss.numpy())

综合对比

损失函数	类型	特点	对异常值敏感性	适用场景
MBE	回归	方向敏感，偏差检测	低	系统偏差分析
MAE	回归	鲁棒，梯度恒定	低	含离群点的回归
MSE	回归	放大大误差，梯度变化	高	重视大误差的回归
RMSE	回归	量纲一致，解释性强	高	同MSE，需量纲一致时
Huber Loss	回归	结合MAE和MSE，平衡鲁棒与收敛	中等	少量离群点的回归
Log Cosh Loss	回归	光滑，二阶可导	中等	深度学习回归任务
Binary Cross Entropy	分类	概率优化，标准二分类损失	高	二分类问题
Hinge Loss	分类	最大化分类边界	低	SVM二分类
Cross Entropy Loss	分类	多分类标准损失	高	多分类问题
KL Divergence	分布度量	非对称，衡量分布差异	高	生成模型、分布比较