【李航统计学习】学习笔记第六篇第五章：决策树之CART算法

分类与回归树（classification and regression tree , CART）是应用广泛的决策树学习算法。CART同样由特征选择、树的生成及剪枝组成，既可以用于分类也可以用于回归。

CART是在给定输入随机变量X条件下输出随机变量Y的条件概率分布的方法学习方法。CART假设决策树是二叉树，内部节点特征的取值为“是”和“否”，左分支是取值为“是”的分支，右分支是取值为“否”的分支。

CART算法由以下两步组成：
（1）决策树生成：基于训练数据集生成决策树，生成的决策树要尽量大；
（2）决策树剪枝：用验证数据集对已生成的树进行剪枝并选择最优子树，这时用损失函数最小作为剪枝的标准。

5.5.1 CART生成

决策树的生成就是递归的构建二叉决策树的过程。对回归树用平方误差最小化准则，对分类树用基尼指数（Gini index）最小化准则，进行特征选择，生成二叉树。

1. 回归树的生成
   最小二乘回归树生成算法：
   
2. 分类树的生成

（1）分类树用基尼指数选择最优特征，同时决定该特征的最优二值切分点。

（2）分类问题中，假设有K个类，样本点属于第k类的概率为pk，则概率分布的基尼指数定义为：
对于二分类问题，则概率分布的基尼指数为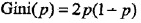：，对于给定的样本D集合，其基尼指数为：这里Ck是D中属于第k类的样本子集，K是类的个数。

（3）如果样本集合D根据特征A是否取某一可能值a被分割成D1和D2两部分，即

则在特征A的条件下，集合D的基尼指数定义为：
基尼指数Gini(D)表示集合D的不确定性，基尼指数Gini(D,A)表示经A=a分割后集合D的不确定性。基尼指数越大，样本集合的不确定性就越大，这一点与熵相似。

（4）CART生成算法

5.5.2 CART剪枝

CART算法从“完全生长”的决策树的底端减去一些子树，使决策树变小（模型变得简单），从而能够对未知数据有更准确的预测。

CART剪枝算法由两步组成：首先是从生成算法产生的决策树T0地段开始不断剪枝，直到T0的根节点，形成一个子树序列{T0,T1,T2…Tn}；然后通过交叉验证法在独立的验证数据集上对字数序列进行测试，从中选择最优子树。

1. 剪枝，形成一个子树序列
（1）从整体树T0开始剪枝。对T0的任意内部结点t,以t为单节点树的损失函数为：
以t为根节点的子树Tt的损失函数为：

当α=0即α充分小时，有
当α增大时，在某一α有
当α在增大时，不等式反向。只要，Tt与t有相同的损失函数值，而t的节点少，因此t比Tt更可取，对Tt进行剪枝。

（2）对T0中每一内部节点t，计算，在T0中剪去g(t)最小的Tt，将得到的子树作为T1，同时将最小的g(t)设为a1，T1为区间[a1,a2) 的最优子树。如此剪枝下去，直到根节点，不断增加a的值，产生新的区间。

2. 在剪枝得到的子树序列T0,T1…Tn中通过交叉验证选取得到最优子树Tα

利用独立的验证数据集，测试子树序列T0,T1…Tn中各棵子树的平方误差或基尼指数。平方误差或基尼指数最小的决策树被认为是最优的决策树。当最优子树Tk确定时，对应的αk也确定了，即得到最优决策树Tα.

3. CART剪枝算法