argument of the maximum/minimum
arg max f(x): 当f(x)取最大值时,x的取值
arg min f(x):当f(x)取最小值时,x的取值
表示使目标函数取最小值时的变量值
From Wikipedia
In mathematics, arg max (or argmax) stands for the argument of the maximum, that is to say, the set of points of the given argument for which the value of the given expression attains its maximum value:[note 1]
In other words,
is the set of values of x for which f(x) has the largest value M. For example, if f(x) is 1−|x|, then it attains its maximum value of 1 at x = 0 and only there, so 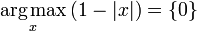 .
.
Equivalently, if M is the maximum of f, then the arg max is the level set of the maximum:
If the maximum is reached at a single value, then one refers to the point as the arg max, meaning we define the arg max as a point, not a set of points. So, for example,
-
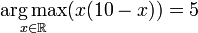 //只有一个值使函数取最大值,则arg为该值
//只有一个值使函数取最大值,则arg为该值
(rather than the singleton set {5}), since the maximum value of x(10 − x) is 25, which happens when x = 5.[note 2]
However, in case the maximum is reached at many values, arg max is a set of points.
Then, we have for example
-
![\underset{x \in [0,4\pi]}{\operatorname{arg\,max}} \, \cos(x) = \{0,2\pi,4\pi\}](http://upload.wikimedia.org/math/0/c/9/0c99d783a9fe097e42c3c38b2a1c0dd5.png) //若多个值使函数取最大值,则arg为集合
//若多个值使函数取最大值,则arg为集合
since the maximum value of cos(x) is 1, which happens on this interval when x = 0, 2π or 4π. On the whole real line, the arg max is 
arg min (or argmin) is defined analogously.
Note also that functions do not in general attain a maximum value, and hence will in general not have an arg max: 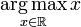 is undefined, as x is unbounded on the real line. However, by the extreme value theorem (or the classical compactness argument), a continuous function on a compact interval has a maximum, and thus an arg max. //若无法取到最大值,无定义
is undefined, as x is unbounded on the real line. However, by the extreme value theorem (or the classical compactness argument), a continuous function on a compact interval has a maximum, and thus an arg max. //若无法取到最大值,无定义
转自:http://www.cppblog.com/guijie/archive/2010/12/13/136273.aspx




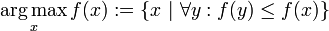


















 3405
3405


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?







