一、冒泡排序
O(n2) S(1) 稳定
算法思想:先遍历0到N-1,若前者大于后者则交换,一次后最大值在N-1的位置。依次类推。
public class BubbleSort {
public static void bubbleSort(int[] arr) {
if(arr == null || arr.length < 2) {
return;
}
for(int e = arr.length - 1; e > 0; e--) {
for(int i = 0; i < e; i++) {
if(arr[i] > arr[i+1]) {
swap(arr,i,i+1);
}
}
}
}
public static void swap(int[] arr,int i,int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}二、选择排序
O(n2) S(1) 不稳定
算法思想:先遍历0到N-1,找到最小的放到第一个,以此类推。
public class SelectionSort {
public static void selectionSort(int[] arr) {
if(arr == null || arr.length < 2) {
return;
}
for(int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
for(int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[minIndex]){
minIndex = j;
}
}
swap(arr,i,minIndex);
}
}
public static void swap(int[] arr,int i,int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
三、插入排序
O(n2) S(1) 稳定
算法思想:认为第一个元素有序,后面的元素依次插入前面的有序区。
public class InsertionSort {
public static void insertionSort(int[] arr) {
if(arr == null || arr.length < 2) {
return;
}
for(int i = 1; i < arr.length; i++) {
for(int j = i; j > 0 && arr[j] < arr[j -1]; j--) {
swap(arr,j,j-1);
}
}
}
public static void swap(int[] arr,int i,int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
四、归并排序
O(nlogn) S(n) 稳定
算法思想:分治,对两边的有序数组进行合并。
public class MergeSort {
public static void mergeSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
mergeSort(arr, 0, arr.length - 1);
}
public static void mergeSort(int[] arr, int l, int r) {
if (l == r) {
return;
}
int mid = l + ((r - l) >> 1);
mergeSort(arr, l, mid);
mergeSort(arr, mid + 1, r);
merge(arr, l, mid, r);
}
public static void merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
while (p1 <= m && p2 <= r) {
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[l + i] = help[i];
}
}
}五、快速排序
O(nlogn) S(logn) 不稳定
算法思想:
(1)partition:随机选择一个元素pviot,使得小于pviot的元素在左边,大于pviot的元素在右边,这样就确定了pviot在整个数组中的位置。
(2)对左右两边数组进行递归调用。
public class QuickSort {
public static void quickSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
quickSort(arr, 0, arr.length - 1);
}
public static void quickSort(int[] arr, int l, int r) {
if (l >= r) {
return;
}
//swap(arr, l + (int) (Math.random() * (r - l + 1)), r);
int j = partition(arr, l, r);
quickSort(arr, l, j - 1);
quickSort(arr, j + 1, r);
}
public static int partition(int[] arr, int l, int r) {
int pivot = arr[l];
int i = l;
int j = r;
while(i < j) {
while(i < j && arr[j] >= pivot) {
j--;
}
while(i < j && arr[i] <= pivot) {
i++;
}
if (i < j) {
swap(arr, i, j);
}
}
swap(arr, l, j);
return j;
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}六、堆排序
O(NlogN) S(1)不稳定
算法思想:将数组构建成堆。然后交换堆顶元素(A[0])和堆的最后的元素((A[N-1])),然后对A[0...N-2]进行堆调整,在交换堆顶元素(A[0])和堆的最后的元素((A[N-2])),直至数组有序。
public class HeapSort {
public static void heapSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 0; i < arr.length; i++) {
heapInsert(arr, i);
}
int size = arr.length;
swap(arr, 0, --size);
while (size > 0) {
heapify(arr, 0, size);
swap(arr, 0, --size);
}
}
public static void heapInsert(int[] arr, int index) {
//大于根节点则交换
while (arr[index] > arr[(index - 1) / 2]) {
swap(arr, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
//根节点和左右孩子中的最大值比,如果大于根节点则交换
public static void heapify(int[] arr, int index, int size) {
int left = index * 2 + 1;
while (left < size) {
int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
largest = arr[largest] > arr[index] ? largest : index;
if (largest == index) {
break;
}
swap(arr, largest, index);
index = largest;
left = index * 2 + 1;
}
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}
七、总结
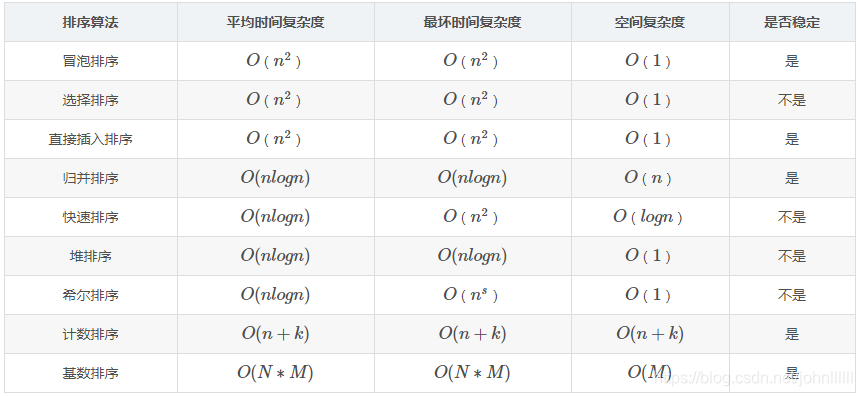
元素的移动次数与关键字的初始排列次序无关的是:基数排序
元素的比较次数与初始序列无关是:选择排序
算法的时间复杂度与初始序列无关的是:直接选择排序
https://www.nowcoder.com/questionTerminal/16e660c81e2c43958961f8222375f384





 本文详细介绍了七种经典的排序算法,包括冒泡排序、选择排序、插入排序、归并排序、快速排序、堆排序和基数排序。每种算法都附有具体的实现代码,并对算法的时间复杂度、空间复杂度及稳定性进行了分析。
本文详细介绍了七种经典的排序算法,包括冒泡排序、选择排序、插入排序、归并排序、快速排序、堆排序和基数排序。每种算法都附有具体的实现代码,并对算法的时间复杂度、空间复杂度及稳定性进行了分析。
















 58万+
58万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








