简单易懂，单调栈和队列

”明月如霜，好风如水，清景无限 “

文远已经很久没更新了，中秋补一篇吧。最常见的两种数据结构，栈和队列，也就是先进后出和先进先出。从这一点来看，似乎这两个数据结构挺简单的，但难点在于何时使用它，也就是识别出什么时候该用这样的数据结构。

壹

* stack基础的基础操作：

• 如果用数组模拟栈的话，需要数组int stk[N] , hh = -1;其中hh = -1待定，也就是初始情况下栈为空，认为stk[0]为栈的首元素。若改为0，则认为stk[1]为栈的首元素。

• 入栈：

stk[++hh] = x;

• 出栈：

--hh;

• 访问栈顶：

cout<<stk[hh]<<endl;

• 判断栈空：

if(hh < 0) ----> 栈空

贰

* 单调栈，顾名思义，具有单调性。而有单调性最大的好处不外乎降低复杂度。相当于排好序了。

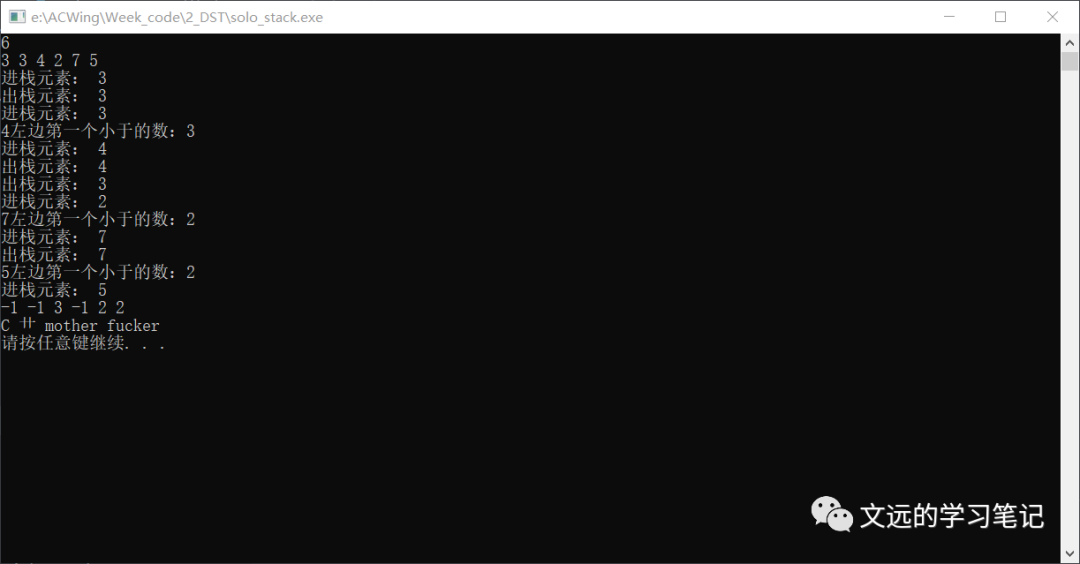
• 最常见应用：找到数组中某数，比其小且index最接近的数。（eg:对长度为N的数组，输出每个数左边第一个比它小的数，没有则输出-1）

• 分析：暴力做，比较简单。双指针：i++循环，j = i并–循环。找到小于的数 ，也就是a[j],就退出内循环。

• 用单调栈做，如何保证栈内单调？输出的答案肯定是栈顶（栈只能输出栈顶）。其实也就是两方面，何时入栈，何时出栈。首先栈顶肯定是最小值。

• 何时出栈：为保证栈顶最小值，新来的小于等于栈顶，那就把内元素给踢出去。很明显这是一个while，也就是持续踢出去

• 何时入栈：新来的严格大于栈顶（则栈顶为离新来的最近的小于它的元素），而且必须入栈在循环末尾。因为需要保证栈内元素是新来的以前的元素（即数左边比它小）。

• 代码：

for(int i = 0 ; i < n ;++i){
    while(hh >= 0 && stk[hh] >= a[i]) {
        cout<<"出栈元素："<<stk[hh]<<endl;
        --hh;
    }
    if(hh >= 0) cout<<stk[hh]<<" ";
    else cout<<"-1 ";
    // if(hh < 0 || a[i] > a[i - 1]) {////栈空则入栈
    // if(hh < 0 || a[i] > stk[hh]) {
        stk[++hh] = a[i];
        cout<<"进栈元素："<<stk[hh]<<endl;
    // }

• 结果：

叁

* queue基础的基础操作：

• 如果用数组模拟队列的话，需要数组int q[N] , hh = 0 , tt = -1;其中队首hh = 0 , 队尾tt = -1;也就是初始情况下队列为空。

• 入队：

q[++tt] = x;

• 出队首：

++hh;

• 出队尾

--tt;

• 访问队首：

cout<<q[hh]<<endl;

• 判断队空：

if(hh > tt) ----> 队空

肆

* 单调队列，顾名思义，具有单调性。而有单调性最大的好处不外乎降低复杂度。相当于排好序了。

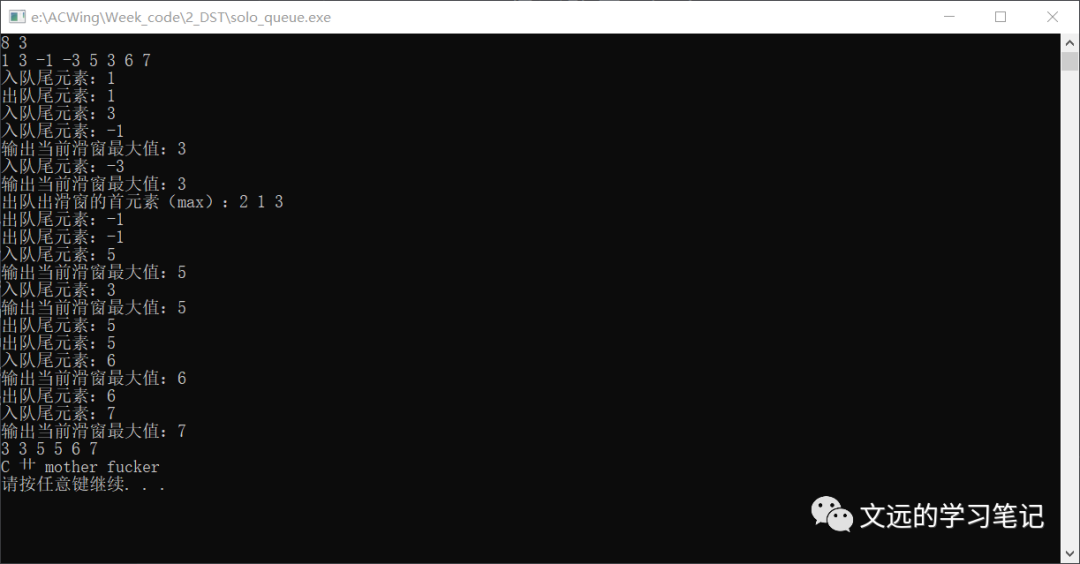
• 最常见应用：找到数组中某个滑动窗口的最小值或者最大值，例如滑动窗口长度为3。（eg:对长度为N的数组，输出长度为3的滑动窗口的最大值）

• 分析：暴力做，比较简单。双指针：i++循环，j = i + 2并++循环。找到[i , j ]内最大值就退出内循环。

• 用单调队列做，如何保证栈内单调？输出的答案肯定是队首（队列一般都是队首出队）。其实也就是两方面，何时入队，何时出队。首先队首肯定是最大值。

• 何时出队：为保证队首最大值，新来的大于等于队尾，否则把队尾元素给踢出去。很明显这是一个while，也就是持续踢出去。另一种则是虽然是最大值，但是滑窗左边界已经离开了最大值，则从队首出队。

• 何时入队：新来的严格小于队尾。（其实还是意思是队内从hh到tt严格下降，而新来的能直接入队尾了，就是因为while把队尾小的都踢出去了）

代码：

vector<int> res;
hh = 0 , tt = -1;
/////队首内存的是a[i --- i + k -1]的最大值下标 
for(int i = 0 ; i < n ;++i){
/////出队：队非空 且 对应新窗口， 窗口左边已过最大值下标 
    if(hh <= tt && i - k + 1 > q[hh]){
        cout<<"出队出滑窗的首元素（max）："<<i - k + 1<<" "<<q[hh]<<" "<<a[q[hh]]<<endl;
        ++hh; 
    }
    ///////保证队尾 大于 a[i]
    while(hh <= tt && a[q[tt]] <= a[i] ){
        cout<<"出队尾元素："<<a[q[hh]]<<endl; 
        --tt;
    }
    q[++tt] = i;
    cout<<"入队尾元素："<<a[i]<<endl; 
    if (i - k + 1 >= 0 && hh <= tt){
        res.push_back(a[q[hh]]);
        cout<<"输出当前滑窗最大值："<<a[q[hh]]<<endl;
    }
}
for(auto i : res){
    cout<<i<<" ";
}
printf("\n");

结果：

获取源码可点击阅读原文，对你有帮助请点赞关注支持一下。

END

作者：不爱跑马的影迷不是好程序猿

   喜欢的话请关注点赞👇 👇👇 👇        

壹句： 昨夜星辰昨夜风

阅读原文