互调失真 ，P1dB 压缩点，三阶交调截止点

        当给放大器输入单音信号(即单频点信号) 时，放大器将输出基频及其谐波分量。当输入双音或多音信号时，放大器的非线性将导致不同频率之间进行组合而产生不同的频率成分，这些称为交调失真产物所有的接收机都采用具有固有非线性特性的 RF-IF 信号处理电路，随之而来的影响接收机性能的另外一个重要参数是双音互调失真，当两个大的无用的信号被加入到接收机的天线输入端时， 由于接收机的 RF 段的非线性产生了互调产物的虚假信号，如果这些产物中的一个频率靠进了接收机的工作频率时，它将被当作真实的输入信号被RF-IF 段和解调器处理， 如下图所示：

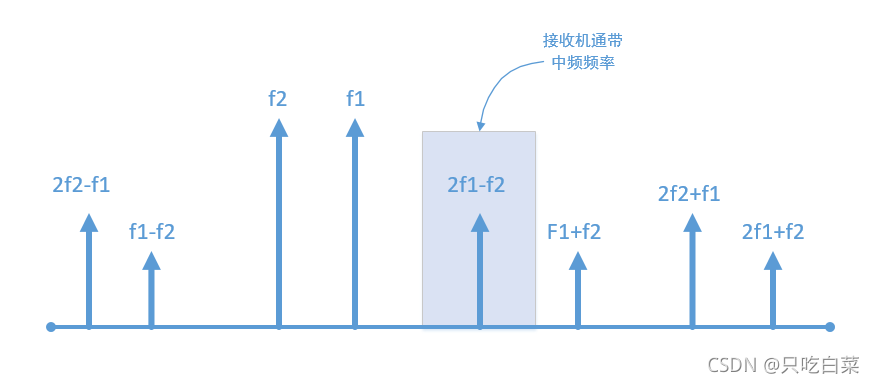
        在接收机的通带频率中，由两个带外干扰信号 f1 和 f2 产生的二阶和三阶双音互调产物，其中二阶和三阶互调失真是主要的失真，特别是具有宽带射频前端的接收机系统，但是如果宽带射频前端如果有信号预选滤波器以衰减在接收机调谐频率上能够产生的互调产物，效果如下图示：

        预选器只是部分的解决了互调失真问题，更麻烦的是当两个同时落入预选器通带内的干扰大信号，将产生落入带内的三阶互调产物（2f1-f2）或者（2f2-f1）中的一个或者两个，虽然减小预选器带宽可以减少接收机受到这种干扰影响的频率范围，但是考虑到我们设备不同于其他常规接收机，可以加尽可能窄的预选器，我们接收机覆盖的带宽远比信号带宽要大得多，这就导致互调失真更加严重且容易出现，因此必须对整个接收机 RF-IF 链路进行适当的电路和系统设计来使问题最小化。
        一般通过给接收机输入两个等功率信号，然后在接收机调谐频率上的失真产物的等效电平来测试接收机的互调指标，但是更加通用衡量失真指标的方法是互调截点来表示。双音三阶互调截点概念可以通过下图来说明：
 

Pin:输入功率
Pout：输出功率
IM3：三阶交调产物
IIP3: 输入三阶交调
OIP3： 输入三阶交调
G：增益
P1dB： 1dB 压缩点
IMD：输出功率和三阶产物 IM3 之差
        上图中蓝色曲线表示基波成分，绿色线条表示三阶交调成分，对于小信号来说蓝色曲线基本上是输入信号增加 1dB 输出信号功率变化 1dB，当输入信号逐渐增大至输入信号增加 2dB 而输出信号仅仅变化 1dB 的时候的这个点叫做 P1dB，即 1DB 压缩点。 绿色曲线的三阶交调分量随着输入信号每增加 1dB，输出增加 3dB， 把两条曲线延长至相交即确定了三阶截点，对应截点处的输入功率电平就是系统的三阶双音互调的输入截点，这个截点数据不能直接测量得到只能通过以下公式计算得出，各指标之间的数学关系如下：

        由上表中 IM3 的计算式可知，如果想要降低三阶交调产物的输出功率，在保证增益以及输入功率不变的情况下只能够去提升三阶截点的数值，接收机的三阶截点越高，就越不容易受带内大信号引起的虚假相应的影响，不幸的是高截点的接收机的常常不能够兼容到同时带来的对低噪声系数的要求，通常这种的办法就是兼顾接收机的噪声系数和三阶截点。 通过对三阶截点的测量可以了解系统的接收性能。