Schröder number(不穿过对角线的路径数 1, 2, 6, 22, 90, 394)

oeis 整数数列大全

Schröder number, describes the number of lattice paths from the southwest corner
( 0 , 0 )of an n × n grid to the northeast corner ( n , n ) , using only single steps north,( 0 , 1 ) ; northeast, ( 1 , 1 ); or east, ( 1 , 0 ), that do not rise above the SW–NE diagonal.

意思是从( 0 , 0 )到( n , n )有多少条不穿过对角线的路径,是不是听起来和卡特兰数很像?
但是这里的路可以是斜着的

Schröder number有以下几种定义:

• S(n)表示第n个Schröder number(S(0)=1,S(1)=2) n*n的方案数

• 从( 0 , 0 )到( 2n , 0 )的方案数

• 过对角线上n点切n刀分成n+1个矩形的方案数

递推公式为:

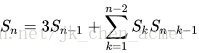
前几项为:

1, 2, 6, 22, 90, 394, 1806, 8558, 41586, 206098, 1037718, 5293446, 27297738, 142078746, 745387038, 3937603038, 20927156706, 111818026018, 600318853926, 3236724317174, 17518619320890, 95149655201962, 518431875418926