约瑟夫环 详解

简介

所有人围成一圈，顺时针报数，每次报到q的人将被杀掉，被杀掉的人将从房间内被移走
然后从被杀掉的下一个人重新报数，继续报q，再清除，直到剩余一人

q = 2

对于q为2的情况，有个简单的方法。
假设$2^n$个人，从1开始数，那么最后活下来的那个一定是1，这个就不证明了。那么可以借用这个规律，假设有9个人，从1开始数，数到2，杀死，接下来到3的时候，相当于8个人从3开始数，那么根据上面的规律，活下来的就是3了（8==$2^3$）

规律为：当q==2时，$2^n+t$个人活下来的是第$2t+1$个人

记得有道q==2，n<=1e100的题，就是可以用这个思路做。需要用大数，找到第一个小于等于$2^x$的数，直接得$ans==2\ast (n-2^x)+1$

---

q != 2

设：$n+1$个数杀每次第q个的最终结果为$A(n+1)$，n个每次杀第q个为$A(n)$
显然$A(n+1)=(A(n)+q)\%(n+1),A(1)==0$

证明：

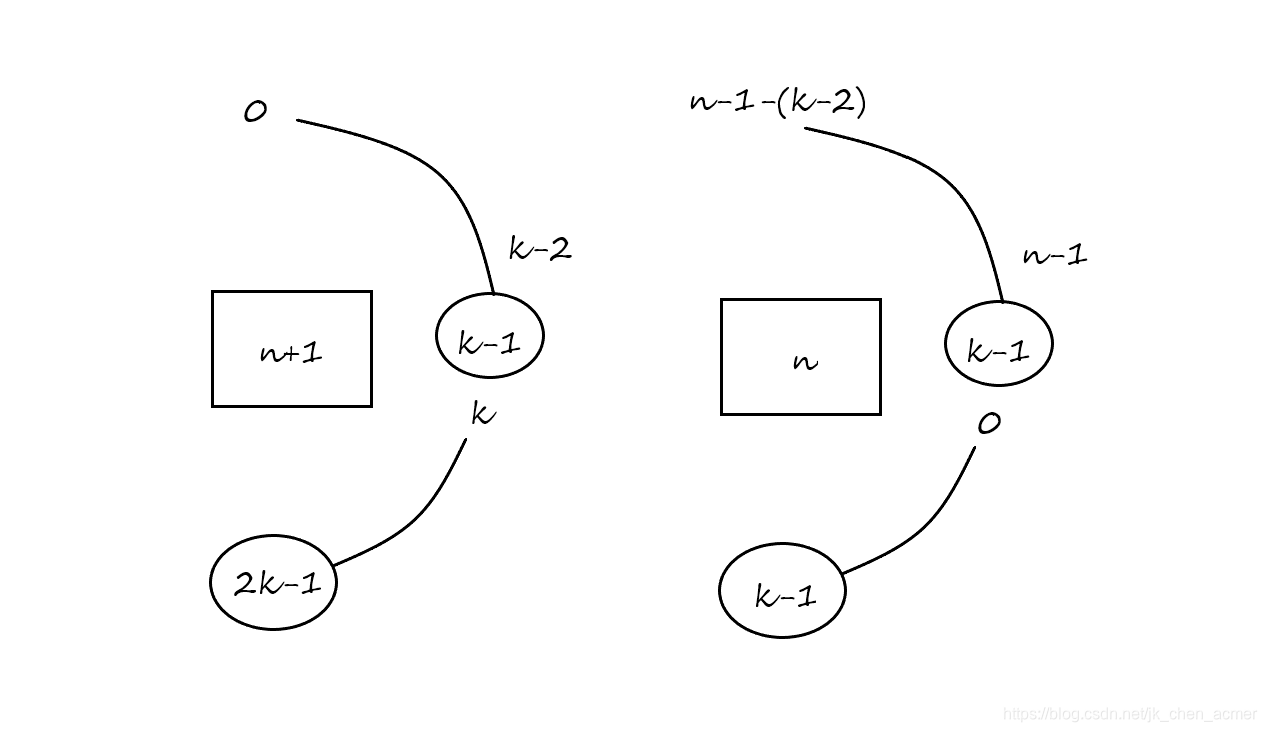
$n+1$个人的游戏中，第一个杀掉的是$k-1$，那么第二个人是$k-1+k$。但是我们可以把杀掉一个人后的情况，看成$n$个人的游戏的开始，也就是说$k-1+k$看成$n$个人的游戏中的$k-1$。所以有$A(n+1)=(A(n)+q)\%(n+1)$

代码：

int f(int n,int q){
    if(n==1){
        return 0;
    }
    return (f(n-1,q)+q)%n;
}//若第一个编号为1，ans++即可