二叉树前序中序 推层序

当然，前序中序不知道的可以自己百度。。。

我们可以知道，知道了一棵二叉树的前序与中序，那么我们便可以推出这棵树的结构（当然，需要保证每个结点的数值不相同）

思路：

假设有前序：4 1 3 2 6 5 7 ，中序：1 2 3 4 5 6 7
那么具体思路为，对于4 1 3 2 6 5 7这棵树，第一个数4是root，那么我们在这棵树的中序1 2 3 4 5 6 7中找到root 4，那么可以得到，中序的root之前的1 2 3就是root的左子树，root后面的5 6 7就是root的右子树，我们再从前序中分出相应个数的结点重复上述流程。
例如：中序1 2 3，对应前序的1 3 2，那么此时root为1，中序的1排在第一个说明1没有左子树，得出1的右子树的中序2 3，前序3 2，root为3，有左子树2，Finished

结构为：

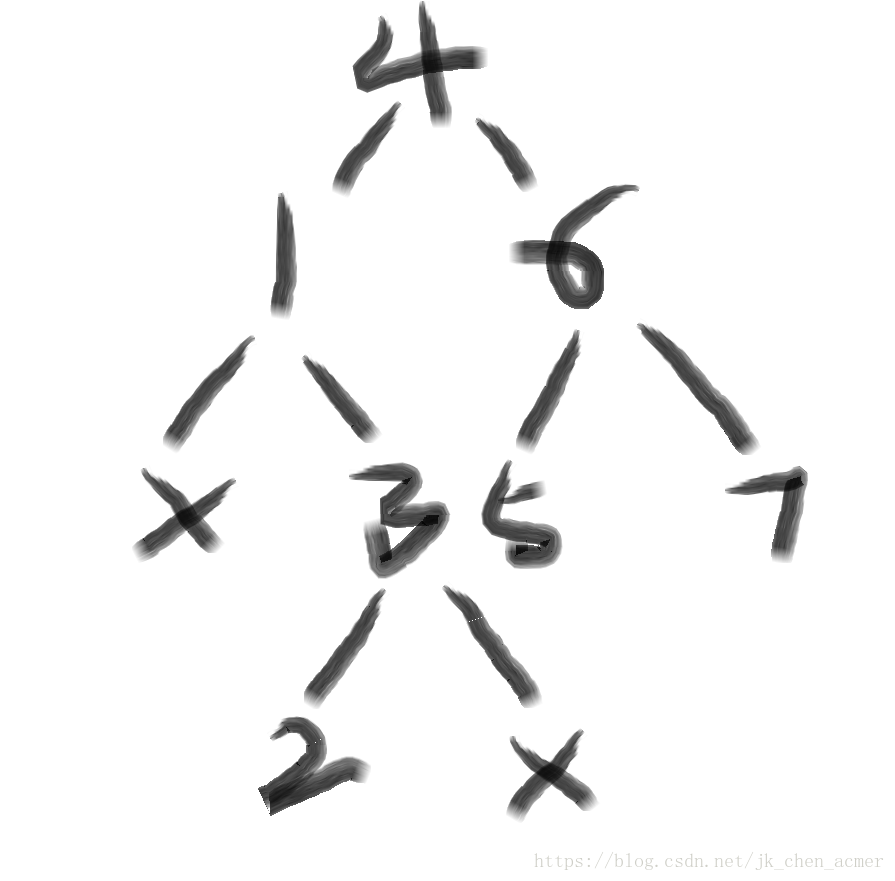
代码：

#include<string>
#include<string.h>
#include<stdio.h>
#include<iostream>
using namespace std;

int n,a[50],b[50],tree[200];
void init(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)scanf("%d",&b[i]);
}
void build(int ro,int l,int r,int fl,int fr){//ro为tree数组下标，l r为b数组范围，fl，fr为a数组范围 
    if(l>r)return;
    int finro;
    for(finro=fl;finro<=fr;finro++){//找到a数组中root（也就是b[l]）的位置 
        if(a[finro]==b[l])break;
    }

    if(l+1<=l+finro-fl)tree[ro<<1]=b[l+1];//没有超出范围的话 

    if(l+finro-fl+1<=r)tree[ro<<1|1]=b[l+finro-fl+1];

    build(ro<<1,l+1,l+finro-fl,fl,finro-1);
    build(ro<<1|1,l+finro-fl+1,r,finro+1,fr);
}
void out(int f){//从右往左输出层序 
    int flag=0;
    for(int i=(1<<f)-1;i>=(1<<(f-1));i--){
        if(tree[i])printf("%d ",tree[i]),flag=1;
    }
    if(flag)out(f+1);
}
int main(){
    init();
    tree[1]=b[1];
    build(1,1,n,1,n);
    out(1);
} 
/*7
1 2 3 4 5 6 7
4 1 3 2 6 5 7*/ 

当然，有用中序和后序推的

思路完全一样，代码如下：

#include<iostream>
#include<stdio.h>
#include<set>
#define D long long
using namespace std;

int tree[200];
int a[50],b[50];
int n;

void build(int ro,int l,int r,int fl,int fr){
    if(l>r)return;
    int i;
    for(i=fl;i<=fr;i++)if(a[i]==b[r])break;
    int lenl=i-fl,lenr=fr-i;

    if(r-1>=r-lenr)tree[ro<<1|1]=b[r-1];
    if(r-1-lenr>=l)tree[ro<<1]=b[r-1-lenr];
    build(ro<<1,l,l+lenl-1,fl,fl+lenl-1);
    build(ro<<1|1,l+lenl,r-1,i+1,fr);

}
void out(int f){//按照层序从左往右输出 
    int fl=0;
    for(int i=(1<<(f-1));i<=1<<(f);i++){
        if(tree[i]){
            printf(" %d",tree[i]);fl=1;
        }
    }
    if(fl)out(f+1);
}
int main(){
    cin>>n;
    for(int i=1;i<=n;i++)scanf("%d",&b[i]);//b 后序 
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    tree[1]=b[n];
    build(1,1,n,1,n);
    printf("%d",b[n]);
    out(2);
    printf("\n");
}